命名由三个共线点 P、Q 和 R 确定的线段。
已知
三个共线点 P、Q 和 R。
任务
我们必须找到它们确定的线段的数量。
解答
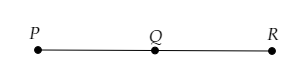
由三个共线点 P、Q 和 R 确定的线段是 $\overline{PQ}、\overline{QR}$ 和 $\overline{PR}$。
- 相关文章
- 给定两点 P 和 Q，求它们确定的线段有多少条？
- 数轴上的点 P、Q、R、S、T、U、A 和 B 使得 $TR = RS = SU$ 且 $AP = PQ = QB$。命名由 P、Q、R 和 S 表示的有理数。
- 点 $P、Q、R$ 和 $S$ 将连接点 $A(1, 2)$ 和 $B(6, 7)$ 的线段分成 5 等份。求点 $P、Q$ 和 $R$ 的坐标。
- 看图，命名以下内容：（1）共线点（2）射线（3）线段（4）直线。写出直线的不同名称。
- 证明点 $P(a, b+c)、Q(b, c+a)$ 和 $R(c, a+b)$ 共线。
- 在 C++ 中最大化长度为 p、q 和 r 的线段数量。
- 命名由点 $P(\sqrt2, \sqrt2)、Q(-\sqrt2, -\sqrt2)$ 和 $R(-\sqrt6, \sqrt6)$ 形成的三角形 $PQR$ 的类型。
- 连接点 $(3, -4)$ 和 $(1, 2)$ 的线段被三等分于点 $P$ 和 $Q$。如果 $P$ 和 $Q$ 的坐标分别为 $(p, -2)$ 和 $(\frac{5}{3}, q)$，求 $p$ 和 $q$ 的值。
- 根据下图，写出标出的点和线段的名称。
- 点 $P$ 和 $Q$ 三等分连接点 $A(-2,0)$ 和 $B(0,8)$ 的线段，使得 $P$ 靠近 $A$。求 $P$ 和 $Q$ 的坐标。
- 如果 $p=-2、q=-1$ 且 $r=3$，求 $p-q-r$ 的值。
- 在三种金属 P、Q 和 R 中，P 的反应性低于 Q，R 的反应性高于 P 和 Q。建议一项活动来按其反应性递减的顺序排列 P、Q 和 R。
- 化简下列式子：a) \( (l^{2}-m^{2})(2 l+m)-m^{3} \) b) \( (p+q+r)(p-q+r)+pq-qr \)
- 设 P 和 Q 是连接点 $A(2, -2)$ 和 $B(-7, 4)$ 的线段的三等分点，其中 P 靠近 A。求 P 和 Q 的坐标。
- 画一个三角形 \( PQR \) 来外接一个半径为 \( 8 \mathrm{~cm} \) 的圆，使得 \( QR \) 被切点 \( T \) 分成的线段 \( QT \) 和 \( TR \) 的长度分别为 \( 14 \mathrm{~cm} \) 和 \( 16 \mathrm{~cm} \)。如果 \( \Delta PQR \) 的面积为 \( 336 \mathrm{~cm}^{2} \)，求边 \( PQ \) 和 \( PR \) 的长度。
数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究