数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究一个正方形的边长为10厘米。求其外接圆和内切圆的面积。
已知
正方形的边长为10厘米。
要求
我们需要求外接圆和内切圆的面积。
解题过程
设正方形为$ABCD$，每条边长为$10\ cm$，$r_1$为外接圆的半径，$r_2$为内切圆的半径。
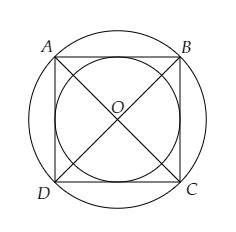
这意味着，
$AB = BC = CD = DA = 10\ cm$
$AC$和$BD$是正方形的对角线。
$\mathrm{AC}=\mathrm{BD}=\sqrt{2}\times10$
$=1.414 \times 10$
$=14.14 \mathrm{~cm}$
外接圆的半径$\mathrm{r_1}=\frac{\mathrm{AC}}{2}$
$=\frac{14.1}{2}$
$=7.05 \mathrm{~cm}$
内切圆的半径$r_2=\frac{\mathrm{AB}}{2}$
$=\frac{10}{2}$
$=5 \mathrm{~cm}$
外接圆的面积$=\pi \mathrm{r_1}^{2}$
$=\frac{22}{7} \times(7.07)^{2}$
$=\frac{22}{7} \times 7.07 \times 7.07$
$=22 \times 1.01 \times 7.07$
$=157.0954$
$=157.1 \mathrm{~cm}^{2}$
内切圆的面积$=\pi r_2^{2}$
$=\frac{22}{7} \times 5 \times 5 \mathrm{~cm}^{2}$
$=\frac{550}{7}$
$=78.57 \mathrm{~cm}^{2}$
外接圆和内切圆的面积分别为$157.1\ cm^2$和$78.57\ cm^2$。
更新于: 2022年10月10日
308 次浏览
广告