TensorFlow - 线性回归

在本章中，我们将重点关注使用 TensorFlow 实现线性回归的基本示例。逻辑回归或线性回归是一种监督机器学习方法，用于对有序离散类别进行分类。我们本章的目标是构建一个模型，用户可以通过该模型预测预测变量和一个或多个自变量之间的关系。

这两个变量之间的关系被认为是线性的。如果 y 是因变量，x 被视为自变量，那么这两个变量的线性回归关系将如下式所示：

Y = Ax+b

我们将为线性回归设计一个算法。这将使我们能够理解以下两个重要概念：

• 成本函数
• 梯度下降算法

线性回归的示意图如下所示：

线性回归方程的图形视图如下所示：

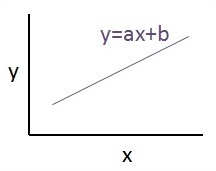
设计线性回归算法的步骤

现在我们将学习有助于设计线性回归算法的步骤。

步骤 1

导入必要的模块以绘制线性回归模块非常重要。我们开始导入 Python 库 NumPy 和 Matplotlib。

import numpy as np 
import matplotlib.pyplot as plt

步骤 2

定义逻辑回归所需的系数数量。

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78

步骤 3

迭代变量以生成回归方程周围的 300 个随机点：

Y = 0.22x+0.78

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y])

步骤 4

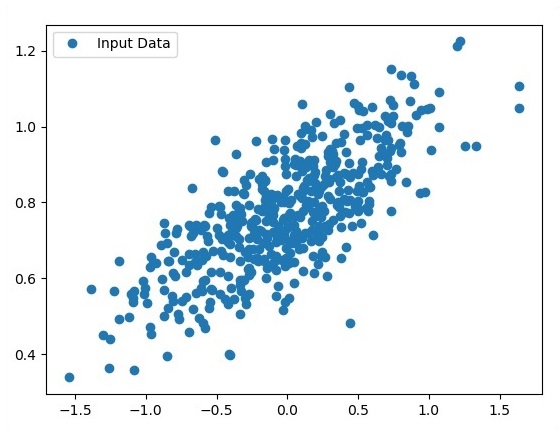
使用 Matplotlib 查看生成的点。

fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()

逻辑回归的完整代码如下：

import numpy as np 
import matplotlib.pyplot as plt 

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78 

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y]) 
   
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() 
plt.show()

作为输入获取的点数被视为输入数据。