- TensorFlow 教程
- TensorFlow - 首页
- TensorFlow - 简介
- TensorFlow - 安装
- 理解人工智能
- 数学基础
- 机器学习与深度学习
- TensorFlow - 基础
- 卷积神经网络
- 循环神经网络
- TensorBoard 可视化
- TensorFlow - 词嵌入
- 单层感知器
- TensorFlow - 线性回归
- TFLearn 及其安装
- CNN 和 RNN 的区别
- TensorFlow - Keras
- TensorFlow - 分布式计算
- TensorFlow - 导出
- 多层感知器学习
- 感知器的隐藏层
- TensorFlow - 优化器
- TensorFlow - XOR 实现
- 梯度下降优化
- TensorFlow - 构建图
- 使用 TensorFlow 进行图像识别
- 神经网络训练建议
- TensorFlow 有用资源
- TensorFlow 快速指南
- TensorFlow - 有用资源
- TensorFlow - 讨论
TensorFlow 快速指南
TensorFlow - 简介
TensorFlow 是一个软件库或框架,由 Google 团队设计,以最简单的方式实现机器学习和深度学习概念。它结合了优化技术的计算代数,可以轻松计算许多数学表达式。
TensorFlow 的官方网站如下所示:
现在让我们考虑 TensorFlow 的以下重要特性:
它包含一个特性,可以借助称为张量的多维数组轻松定义、优化和计算数学表达式。
它包含对深度神经网络和机器学习技术的编程支持。
它包含使用各种数据集进行计算的高可扩展性特性。
TensorFlow 使用 GPU 计算,并自动管理。它还包含一个独特的特性,可以优化相同内存和使用的数据。
为什么 TensorFlow 如此受欢迎?
TensorFlow 文档齐全,包含大量机器学习库。它为此提供了一些重要的功能和方法。
TensorFlow 也被称为“Google”产品。它包含各种机器学习和深度学习算法。TensorFlow 可以训练和运行深度神经网络,用于手写数字分类、图像识别、词嵌入以及创建各种序列模型。
TensorFlow - 安装
要安装 TensorFlow,系统中必须安装“Python”。Python 3.4+ 版本被认为是开始安装 TensorFlow 的最佳版本。
请考虑以下在 Windows 操作系统中安装 TensorFlow 的步骤。
步骤 1 - 验证已安装的 python 版本。
步骤 2 - 用户可以选择任何机制在系统中安装 TensorFlow。我们推荐“pip”和“Anaconda”。Pip 是一个用于在 Python 中执行和安装模块的命令。
在安装 TensorFlow 之前,我们需要在系统中安装 Anaconda 框架。
安装成功后,通过“conda”命令在命令提示符中进行检查。命令执行如下所示:
步骤 3 - 执行以下命令初始化 TensorFlow 的安装:
conda create --name tensorflow python = 3.5
它会下载 TensorFlow 设置所需的必要软件包。
步骤 4 - 环境设置成功后,务必激活 TensorFlow 模块。
activate tensorflow
步骤 5 - 使用 pip 在系统中安装“Tensorflow”。用于安装的命令如下所示:
pip install tensorflow
并且,
pip install tensorflow-gpu
安装成功后,了解 TensorFlow 的示例程序执行非常重要。
以下示例帮助我们理解 TensorFlow 中的基本程序创建“Hello World”。
第一个程序实现的代码如下所示:
>> activate tensorflow >> python (activating python shell) >> import tensorflow as tf >> hello = tf.constant(‘Hello, Tensorflow!’) >> sess = tf.Session() >> print(sess.run(hello))
理解人工智能
人工智能包括机器和特殊计算机系统模拟人类智能的过程。人工智能的例子包括学习、推理和自我纠正。AI 的应用包括语音识别、专家系统以及图像识别和机器视觉。
机器学习是人工智能的一个分支,它处理可以学习任何新数据和数据模式的系统和算法。
让我们关注下面提到的韦恩图,以理解机器学习和深度学习的概念。
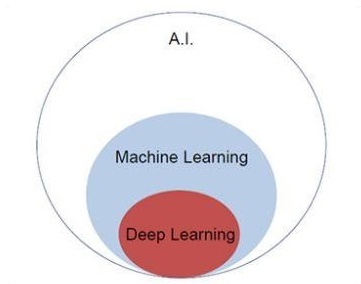
机器学习包含机器学习的一部分,深度学习是机器学习的一部分。遵循机器学习概念的程序的能力是提高其观察数据的性能。数据转换的主要动机是提高其知识,以便在未来获得更好的结果,为该特定系统提供更接近所需输出的输出。机器学习包括“模式识别”,其中包括识别数据中模式的能力。
应训练这些模式以以理想的方式显示输出。
机器学习可以通过两种不同的方式进行训练:
- 监督训练
- 无监督训练
监督学习
监督学习或监督训练包括一个过程,其中训练集作为输入提供给系统,其中每个示例都用所需的输出值进行标记。此类型的训练是使用最小化特定损失函数来执行的,该函数表示相对于所需输出系统的输出误差。
训练完成后,根据与训练集分离的示例(也称为验证集)衡量每个模型的准确性。
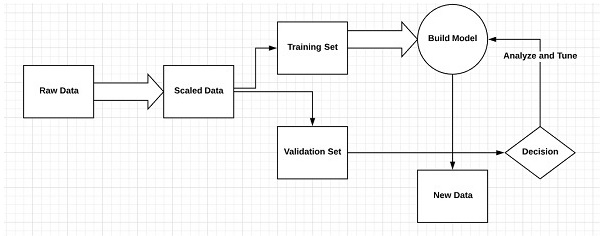
说明“监督学习”的最佳示例是一堆带有包含在其中的信息的图片。在这里,用户可以训练模型来识别新的图片。
无监督学习
在无监督学习或无监督训练中,包括训练示例,这些示例未被系统标记为属于哪个类别。系统查找共享共同特征的数据,并根据内部知识特征更改它们。这种类型的学习算法主要用于聚类问题。
说明“无监督学习”的最佳示例是一堆没有包含信息的图片,用户使用分类和聚类训练模型。这种类型的训练算法在没有提供信息的情况下进行假设。
TensorFlow - 数学基础
在创建 TensorFlow 中的基本应用程序之前,了解 TensorFlow 所需的数学概念非常重要。数学被认为是任何机器学习算法的核心。借助数学的核心概念,可以定义特定机器学习算法的解决方案。
向量
定义为连续或离散的数字数组。机器学习算法处理固定长度的向量以生成更好的输出。
机器学习算法处理多维数据,因此向量起着至关重要的作用。

向量模型的图形表示如下所示:
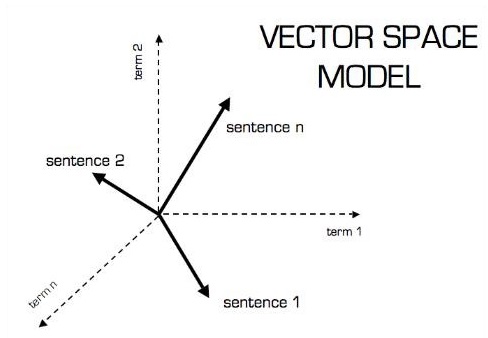
标量
标量可以定义为一维向量。标量是那些仅包含大小而不包含方向的标量。对于标量,我们只关心大小。
标量的示例包括儿童的体重和身高参数。
矩阵
矩阵可以定义为多维数组,以行和列的形式排列。矩阵的大小由行长度和列长度定义。下图显示了任何指定矩阵的表示。
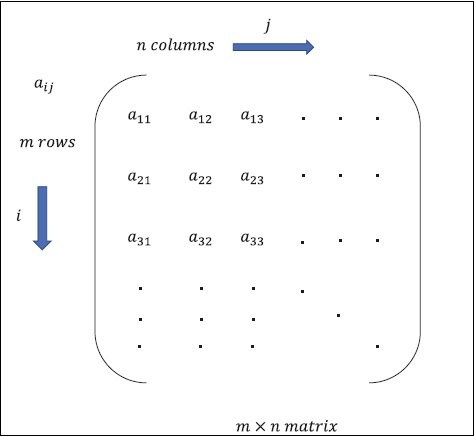
考虑上面提到的具有“m”行和“n”列的矩阵,矩阵表示将指定为“m*n 矩阵”,这也定义了矩阵的长度。
数学计算
在本节中,我们将学习 TensorFlow 中的不同数学计算。
矩阵加法
如果矩阵具有相同的维度,则可以对两个或多个矩阵进行加法。加法意味着根据给定位置对每个元素进行加法。
请考虑以下示例以了解矩阵加法的工作原理:
$$示例:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:那么\:A+B=\begin{bmatrix}1+5 & 2+6 \\3+7 & 4+8 \end{bmatrix}=\begin{bmatrix}6 & 8 \\10 & 12 \end{bmatrix}$$
矩阵减法
矩阵减法与两个矩阵的加法类似。用户可以减去两个矩阵,前提是维度相等。
$$示例:A-\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B-\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:那么\:A-B-\begin{bmatrix}1-5 & 2-6 \\3-7 & 4-8 \end{bmatrix}-\begin{bmatrix}-4 & -4 \\-4 & -4 \end{bmatrix}$$
矩阵乘法
对于两个矩阵 A m*n 和 B p*q 可以相乘,n 应等于 p。生成的矩阵为:
C m*q
$$A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}$$
$$c_{11}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=1\times5+2\times7=19\:c_{12}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=1\times6+2\times8=22$$
$$c_{21}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=3\times5+4\times7=43\:c_{22}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=3\times6+4\times8=50$$
$$C=\begin{bmatrix}c_{11} & c_{12} \\c_{21} & c_{22} \end{bmatrix}=\begin{bmatrix}19 & 22 \\43 & 50 \end{bmatrix}$$
矩阵转置
矩阵 A 的转置,m*n 通常用 AT(转置)n*m 表示,它是通过将列向量转置为行向量获得的。
$$示例:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}\:那么\:A^{T}\begin{bmatrix}1 & 3 \\2 & 4 \end{bmatrix}$$
向量的点积
任何维度为 n 的向量都可以表示为矩阵 v = R^n*1。
$$v_{1}=\begin{bmatrix}v_{11} \\v_{12} \\\cdot\\\cdot\\\cdot\\v_{1n}\end{bmatrix}v_{2}=\begin{bmatrix}v_{21} \\v_{22} \\\cdot\\\cdot\\\cdot\\v_{2n}\end{bmatrix}$$
两个向量的点积是对应分量的乘积之和 - 沿相同维度的分量,可以表示为
$$v_{1}\cdot v_{2}=v_1^Tv_{2}=v_2^Tv_{1}=v_{11}v_{21}+v_{12}v_{22}+\cdot\cdot+v_{1n}v_{2n}=\displaystyle\sum\limits_{k=1}^n v_{1k}v_{2k}$$
向量的点积示例如下所示:
$$示例:v_{1}=\begin{bmatrix}1 \\2 \\3\end{bmatrix}v_{2}=\begin{bmatrix}3 \\5 \\-1\end{bmatrix}v_{1}\cdot v_{2}=v_1^Tv_{2}=1\times3+2\times5-3\times1=10$$
机器学习和深度学习
人工智能是近些年来最流行的趋势之一。机器学习和深度学习构成了人工智能。下面所示的韦恩图解释了机器学习和深度学习的关系:

机器学习
机器学习是让计算机根据设计的算法和程序进行操作的科学艺术。许多研究人员认为机器学习是朝着人类水平人工智能取得进展的最佳途径。机器学习包括以下类型的模式
- 监督学习模式
- 无监督学习模式
深度学习
深度学习是机器学习的一个子领域,其中相关的算法受到称为人工神经网络的大脑结构和功能的启发。
深度学习今天所有的价值都是通过监督学习或从标记数据和算法中学习获得的。
深度学习中的每个算法都经历相同的过程。它包括输入的非线性变换的层次结构,可用于生成作为输出的统计模型。
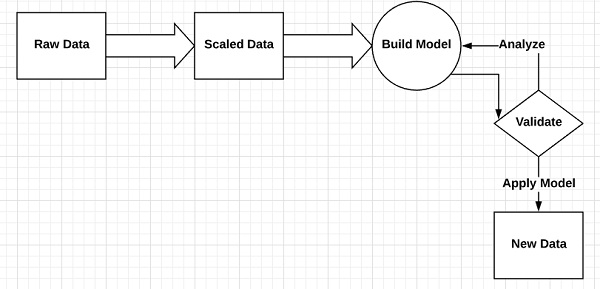
考虑定义机器学习过程的以下步骤
- 识别相关数据集并准备它们进行分析。
- 选择要使用的算法类型
- 基于所使用的算法构建分析模型。
- 在测试数据集上训练模型,并在需要时进行修改。
- 运行模型以生成测试分数。
机器学习和深度学习的区别
在本节中,我们将了解机器学习和深度学习之间的区别。
数据量
机器学习使用大量数据。它也适用于少量数据。另一方面,深度学习如果数据量迅速增加,则可以高效地工作。下图显示了机器学习和深度学习随数据量变化的工作方式 -
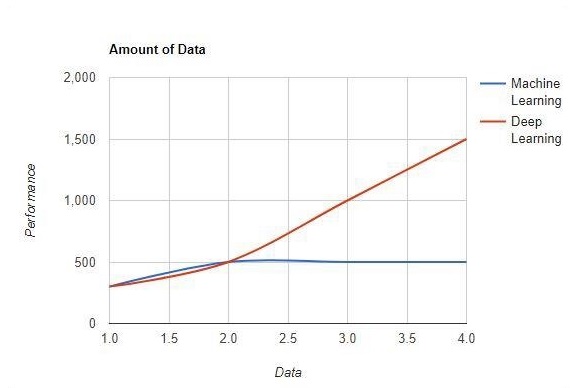
硬件依赖性
与传统的机器学习算法不同,深度学习算法被设计为严重依赖于高端机器。深度学习算法执行大量矩阵乘法运算,这需要大量的硬件支持。
特征工程
特征工程是将领域知识放入指定特征中以降低数据复杂度并使学习算法可见的模式的过程。
例如 - 传统的机器学习模式侧重于像素和其他特征工程过程所需的属性。深度学习算法专注于数据中的高级特征。它减少了为每个新问题开发新的特征提取器的任务。
问题解决方法
传统的机器学习算法遵循标准程序来解决问题。它将问题分解成多个部分,解决每个部分,并将它们组合起来以获得所需的结果。深度学习专注于端到端地解决问题,而不是将其分解成多个部分。
执行时间
执行时间是训练算法所需的时间。深度学习需要大量时间来训练,因为它包含大量参数,这比平时需要更长的时间。机器学习算法相对需要较少的执行时间。
可解释性
可解释性是比较机器学习和深度学习算法的主要因素。主要原因是深度学习在工业应用之前仍然需要谨慎考虑。
机器学习和深度学习的应用
在本节中,我们将学习机器学习和深度学习的不同应用。
计算机视觉,用于人脸识别和通过指纹或车牌识别车辆进行考勤标记。
从搜索引擎中检索信息,例如文本搜索以进行图像搜索。
自动电子邮件营销,并指定目标识别。
癌症肿瘤的医学诊断或任何慢性疾病的异常识别。
自然语言处理,用于照片标记等应用。解释这种情况的最佳示例是在 Facebook 中使用。
在线广告。
未来趋势
随着数据科学和机器学习在行业中使用的趋势不断增强,每个组织将机器学习融入其业务变得越来越重要。
深度学习正变得比机器学习更重要。深度学习被证明是最新性能的最佳技术之一。
机器学习和深度学习将证明对研究和学术领域有益。
结论
在本文中,我们概述了机器学习和深度学习,并配以插图和差异,也重点关注了未来趋势。许多 AI 应用主要利用机器学习算法来推动自助服务、提高座席工作效率以及使工作流程更可靠。机器学习和深度学习算法为许多企业和行业领导者带来了令人兴奋的前景。
TensorFlow - 基础
在本章中,我们将学习 TensorFlow 的基础知识。我们将从了解张量的 数据结构开始。
张量数据结构
张量在 TensorFlow 语言中用作基本数据结构。张量表示任何称为数据流图的流程图中的连接边。张量被定义为多维数组或列表。
张量由以下三个参数标识 -
秩
张量中描述的维度单位称为秩。它标识张量的维度数。张量的秩可以描述为张量定义的阶数或 n 维。
形状
行数和列数一起定义张量的形状。
类型
类型描述分配给张量元素的数据类型。
用户需要考虑以下活动来构建张量 -
- 构建一个 n 维数组
- 转换 n 维数组。
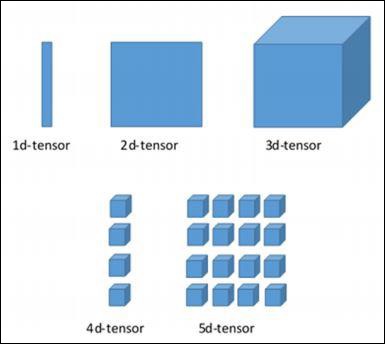
TensorFlow 的各个维度
TensorFlow 包括各种维度。下面简要描述了这些维度 -
一维张量
一维张量是一种普通的数组结构,它包含一组相同数据类型的值。
声明
>>> import numpy as np >>> tensor_1d = np.array([1.3, 1, 4.0, 23.99]) >>> print tensor_1d
下面屏幕截图中显示了带有输出的实现 -
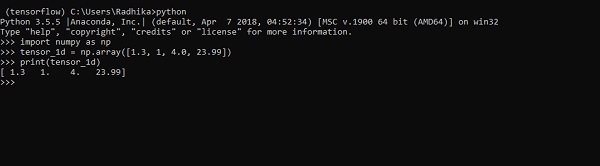
元素的索引与 Python 列表相同。第一个元素的索引从 0 开始;要通过索引打印值,您只需提及索引号。
>>> print tensor_1d[0] 1.3 >>> print tensor_1d[2] 4.0
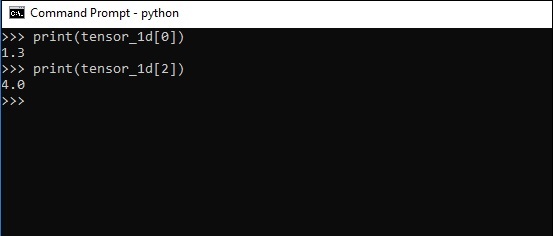
二维张量
一系列数组用于创建“二维张量”。
下面描述了二维张量的创建 -
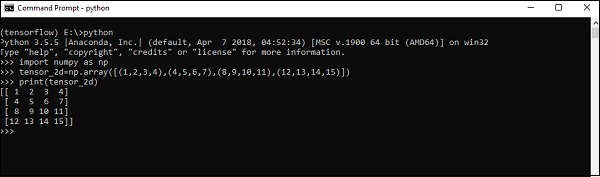
以下是创建二维数组的完整语法 -
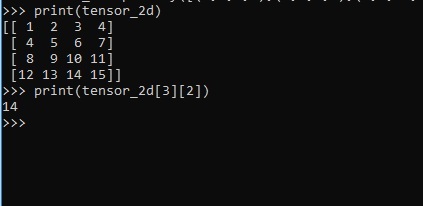
>>> import numpy as np >>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)]) >>> print(tensor_2d) [[ 1 2 3 4] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]] >>>
可以通过指定为索引号的行号和列号来跟踪二维张量的特定元素。
>>> tensor_2d[3][2] 14
张量处理和操作
在本节中,我们将学习张量处理和操作。
首先,让我们考虑以下代码 -
import tensorflow as tf import numpy as np matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32') matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32') print (matrix1) print (matrix2) matrix1 = tf.constant(matrix1) matrix2 = tf.constant(matrix2) matrix_product = tf.matmul(matrix1, matrix2) matrix_sum = tf.add(matrix1,matrix2) matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32') print (matrix_3) matrix_det = tf.matrix_determinant(matrix_3) with tf.Session() as sess: result1 = sess.run(matrix_product) result2 = sess.run(matrix_sum) result3 = sess.run(matrix_det) print (result1) print (result2) print (result3)
输出
以上代码将生成以下输出 -
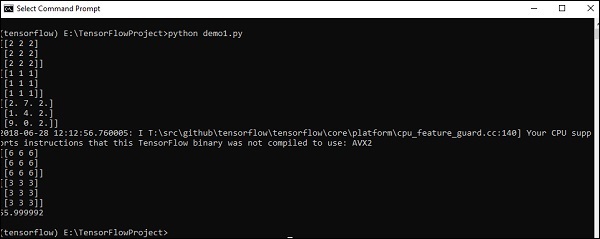
解释
我们在上面的源代码中创建了多维数组。现在,重要的是要理解我们创建了图和会话,它们管理张量并生成相应的输出。借助图,我们获得了指定张量之间数学计算的输出。
TensorFlow - 卷积神经网络
在理解机器学习概念之后,我们现在可以将注意力转移到深度学习概念上。深度学习是机器学习的一个分支,被认为是近几十年来研究人员采取的关键步骤。深度学习实现的示例包括图像识别和语音识别等应用。
以下是两种重要的深度神经网络类型 -
- 卷积神经网络
- 循环神经网络
在本章中,我们将重点关注 CNN,即卷积神经网络。
卷积神经网络
卷积神经网络旨在通过多层数组处理数据。这种类型的神经网络用于图像识别或人脸识别等应用。CNN 与任何其他普通神经网络的主要区别在于,CNN 将输入作为二维数组,并直接对图像进行操作,而不是专注于其他神经网络所关注的特征提取。
CNN 的主要方法包括解决识别问题的方案。谷歌和 Facebook 等顶级公司已投资于识别项目的研发,以更快地完成活动。
卷积神经网络使用三个基本思想 -
- 局部感受野
- 卷积
- 池化
让我们详细了解这些想法。
CNN 利用输入数据中存在的空间相关性。神经网络的每个并发层都连接一些输入神经元。这个特定区域称为局部感受野。局部感受野侧重于隐藏神经元。隐藏神经元处理上述字段内的输入数据,而没有意识到特定边界之外的变化。
以下是生成局部感受野的图表表示 -
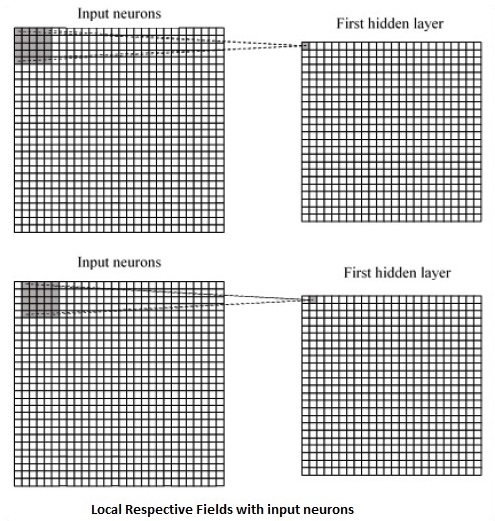
如果我们观察上述表示,每个连接都会学习隐藏神经元与从一层到另一层移动的相关连接的权重。在这里,单个神经元会不时地发生偏移。此过程称为“卷积”。
从输入层到隐藏特征图的连接映射被定义为“共享权重”,包含的偏差称为“共享偏差”。
CNN 或卷积神经网络使用池化层,这些层是 CNN 声明后立即放置的层。它将用户的输入作为来自卷积网络的特征图,并准备一个浓缩的特征图。池化层有助于创建具有前一层神经元的层。
CNN 的 TensorFlow 实现
在本节中,我们将学习 CNN 的 TensorFlow 实现。执行整个网络并使其具有适当维度所需的步骤如下所示 -
步骤 1 - 包括 TensorFlow 和数据集模块所需的模块,这些模块是计算 CNN 模型所必需的。
import tensorflow as tf import numpy as np from tensorflow.examples.tutorials.mnist import input_data
步骤 2 - 声明一个名为 run_cnn() 的函数,该函数包含各种参数和优化变量以及数据占位符的声明。这些优化变量将声明训练模式。
def run_cnn():
mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
learning_rate = 0.0001
epochs = 10
batch_size = 50
步骤 3 - 在此步骤中,我们将使用输入参数声明训练数据占位符 - 对于 28 x 28 像素 = 784。这是从 mnist.train.nextbatch() 中提取的扁平化图像数据。
我们可以根据需要重新整形张量。第一个值 (-1) 告诉函数根据传递给它的数据量动态地整形该维度。两个中间维度设置为图像大小(即 28 x 28)。
x = tf.placeholder(tf.float32, [None, 784]) x_shaped = tf.reshape(x, [-1, 28, 28, 1]) y = tf.placeholder(tf.float32, [None, 10])
步骤 4 - 现在,重要的是创建一些卷积层 -
layer1 = create_new_conv_layer(x_shaped, 1, 32, [5, 5], [2, 2], name = 'layer1') layer2 = create_new_conv_layer(layer1, 32, 64, [5, 5], [2, 2], name = 'layer2')
步骤 5 - 让我们将输出展平以准备好用于全连接输出阶段 - 在两层步长为 2 的池化之后,维度为 28 x 28,到维度为 14 x 14 或最小 7 x 7 x,y 坐标,但有 64 个输出通道。要使用“密集”层创建全连接,新形状需要为 [-1, 7 x 7 x 64]。我们可以为此层设置一些权重和偏差值,然后使用 ReLU 激活。
flattened = tf.reshape(layer2, [-1, 7 * 7 * 64]) wd1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1000], stddev = 0.03), name = 'wd1') bd1 = tf.Variable(tf.truncated_normal([1000], stddev = 0.01), name = 'bd1') dense_layer1 = tf.matmul(flattened, wd1) + bd1 dense_layer1 = tf.nn.relu(dense_layer1)
步骤 6 - 另一个具有特定 softmax 激活的层以及所需的优化器定义了准确性评估,这使得初始化运算符的设置成为可能。
wd2 = tf.Variable(tf.truncated_normal([1000, 10], stddev = 0.03), name = 'wd2') bd2 = tf.Variable(tf.truncated_normal([10], stddev = 0.01), name = 'bd2') dense_layer2 = tf.matmul(dense_layer1, wd2) + bd2 y_ = tf.nn.softmax(dense_layer2) cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(logits = dense_layer2, labels = y)) optimiser = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cross_entropy) correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) init_op = tf.global_variables_initializer()
步骤 7 - 我们应该设置记录变量。这增加了一个摘要来存储数据的准确性。
tf.summary.scalar('accuracy', accuracy)
merged = tf.summary.merge_all()
writer = tf.summary.FileWriter('E:\TensorFlowProject')
with tf.Session() as sess:
sess.run(init_op)
total_batch = int(len(mnist.train.labels) / batch_size)
for epoch in range(epochs):
avg_cost = 0
for i in range(total_batch):
batch_x, batch_y = mnist.train.next_batch(batch_size = batch_size)
_, c = sess.run([optimiser, cross_entropy], feed_dict = {
x:batch_x, y: batch_y})
avg_cost += c / total_batch
test_acc = sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
mnist.test.labels})
summary = sess.run(merged, feed_dict = {x: mnist.test.images, y:
mnist.test.labels})
writer.add_summary(summary, epoch)
print("\nTraining complete!")
writer.add_graph(sess.graph)
print(sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
mnist.test.labels}))
def create_new_conv_layer(
input_data, num_input_channels, num_filters,filter_shape, pool_shape, name):
conv_filt_shape = [
filter_shape[0], filter_shape[1], num_input_channels, num_filters]
weights = tf.Variable(
tf.truncated_normal(conv_filt_shape, stddev = 0.03), name = name+'_W')
bias = tf.Variable(tf.truncated_normal([num_filters]), name = name+'_b')
#Out layer defines the output
out_layer =
tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding = 'SAME')
out_layer += bias
out_layer = tf.nn.relu(out_layer)
ksize = [1, pool_shape[0], pool_shape[1], 1]
strides = [1, 2, 2, 1]
out_layer = tf.nn.max_pool(
out_layer, ksize = ksize, strides = strides, padding = 'SAME')
return out_layer
if __name__ == "__main__":
run_cnn()
以下是上述代码生成的输出 -
See @{tf.nn.softmax_cross_entropy_with_logits_v2}.
2018-09-19 17:22:58.802268: I
T:\src\github\tensorflow\tensorflow\core\platform\cpu_feature_guard.cc:140]
Your CPU supports instructions that this TensorFlow binary was not compiled to
use: AVX2
2018-09-19 17:25:41.522845: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.
2018-09-19 17:25:44.630941: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 501760000 exceeds 10% of system memory.
Epoch: 1 cost = 0.676 test accuracy: 0.940
2018-09-19 17:26:51.987554: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.
TensorFlow - 循环神经网络
循环神经网络是一种面向深度学习的算法,它遵循顺序方法。在神经网络中,我们总是假设每个输入和输出都独立于所有其他层。这类神经网络被称为循环神经网络,因为它们以顺序方式执行数学计算。
考虑以下训练循环神经网络的步骤:
步骤 1 - 从数据集中输入一个特定示例。
步骤 2 - 网络将获取一个示例,并使用随机初始化的变量进行一些计算。
步骤 3 - 然后计算预测结果。
步骤 4 - 生成的实际结果与期望值的比较将产生误差。
步骤 5 - 为了跟踪误差,它会通过相同的路径传播,其中变量也会被调整。
步骤 6 - 重复步骤 1 到 5,直到我们确信声明以获取输出的变量已正确定义。
步骤 7 - 通过应用这些变量来获取新的未见输入,从而进行系统预测。
下面描述了表示循环神经网络的示意图方法:
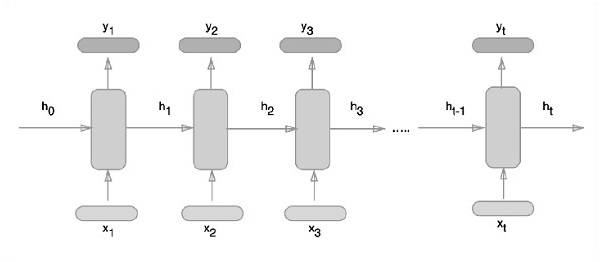
使用 TensorFlow 实现循环神经网络
在本节中,我们将学习如何使用 TensorFlow 实现循环神经网络。
步骤 1 - TensorFlow 包含用于循环神经网络模块的特定实现的各种库。
#Import necessary modules
from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
如上所述,这些库有助于定义输入数据,这是循环神经网络实现的主要部分。
步骤 2 - 我们的主要目的是使用循环神经网络对图像进行分类,其中我们将每张图像的行视为像素序列。MNIST 图像形状被特别定义为 28*28 px。现在我们将处理每个样本提到的 28 个序列的 28 个步骤。我们将定义输入参数以完成顺序模式。
n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10
# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([n_classes]))
}
步骤 3 - 使用 RNN 中定义的函数计算结果以获得最佳结果。在这里,每个数据形状都与当前输入形状进行比较,并计算结果以保持准确率。
def RNN(x, weights, biases): x = tf.unstack(x, n_steps, 1) # Define a lstm cell with tensorflow lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0) # Get lstm cell output outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32) # Linear activation, using rnn inner loop last output return tf.matmul(outputs[-1], weights['out']) + biases['out'] pred = RNN(x, weights, biases) # Define loss and optimizer cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y)) optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost) # Evaluate model correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1)) accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32)) # Initializing the variables init = tf.global_variables_initializer()
步骤 4 - 在此步骤中,我们将启动图形以获取计算结果。这也有助于计算测试结果的准确性。
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x.reshape((batch_size, n_steps, n_input))
sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
if step % display_step == 0:
# Calculate batch accuracy
acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
# Calculate batch loss
loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
step += 1
print("Optimization Finished!")
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
test_label = mnist.test.labels[:test_len]
print("Testing Accuracy:", \
sess.run(accuracy, feed_dict={x: test_data, y: test_label}))
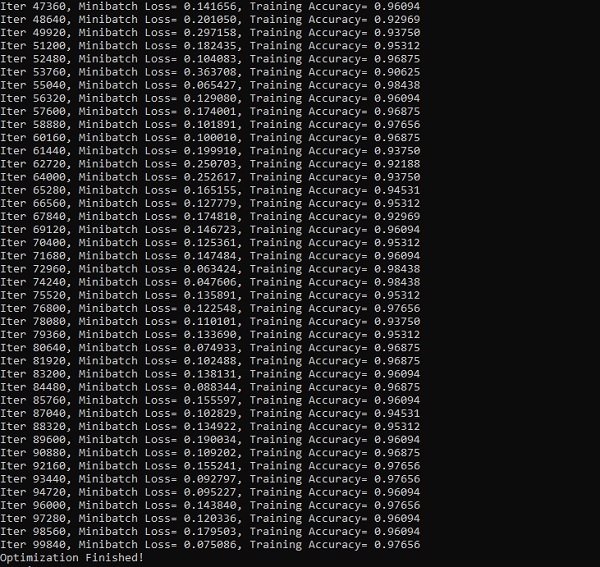
以下屏幕截图显示了生成的输出:
TensorFlow - TensorBoard 可视化
TensorFlow 包含一个可视化工具,称为 TensorBoard。它用于分析数据流图,也用于理解机器学习模型。TensorBoard 的重要功能包括查看关于参数的不同类型的统计信息以及任何图形的垂直对齐细节。
深度神经网络包含多达 36,000 个节点。TensorBoard 有助于将这些节点折叠到高级块中并突出显示相同的结构。这允许更好地分析图形,重点关注计算图的主要部分。TensorBoard 可视化被认为是非常交互式的,用户可以平移、缩放和展开节点以显示详细信息。
以下示意图表示显示了 TensorBoard 可视化的完整工作原理:
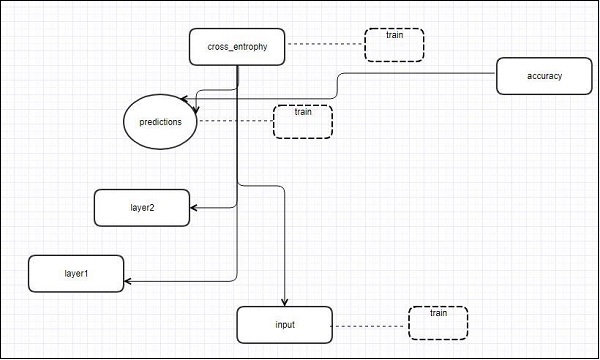
这些算法将节点折叠成高级块,并突出显示具有相同结构的特定组,这些组将高级节点分开。因此创建的 TensorBoard 很有用,并且被视为调整机器学习模型同等重要。此可视化工具专为包含摘要信息和需要显示的详细信息的配置日志文件而设计。
让我们借助以下代码重点关注 TensorBoard 可视化的演示示例:
import tensorflow as tf
# Constants creation for TensorBoard visualization
a = tf.constant(10,name = "a")
b = tf.constant(90,name = "b")
y = tf.Variable(a+b*2,name = 'y')
model = tf.initialize_all_variables() #Creation of model
with tf.Session() as session:
merged = tf.merge_all_summaries()
writer = tf.train.SummaryWriter("/tmp/tensorflowlogs",session.graph)
session.run(model)
print(session.run(y))
下表显示了用于节点表示的 TensorBoard 可视化的各种符号:

TensorFlow - 词嵌入
词嵌入是将离散对象(如单词)映射到向量和实数的概念。它对于机器学习的输入很重要。该概念包括标准函数,这些函数可以有效地将离散输入对象转换为有用的向量。
词嵌入输入的示例图如下所示:
blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259) blues: (0.01396, 0.11887, -0.48963, ..., 0.033483, -0.10007, 0.1158) orange: (-0.24776, -0.12359, 0.20986, ..., 0.079717, 0.23865, -0.014213) oranges: (-0.35609, 0.21854, 0.080944, ..., -0.35413, 0.38511, -0.070976)
Word2vec
Word2vec 是用于无监督词嵌入技术的最常用方法。它以这样一种方式训练模型:给定一个输入词,通过使用跳跃语法来预测该词的上下文。
TensorFlow 提供了许多方法来实现这种模型,这些方法具有越来越高的复杂性和优化水平,并使用多线程概念和更高级别的抽象。
import os
import math
import numpy as np
import tensorflow as tf
from tensorflow.contrib.tensorboard.plugins import projector
batch_size = 64
embedding_dimension = 5
negative_samples = 8
LOG_DIR = "logs/word2vec_intro"
digit_to_word_map = {
1: "One",
2: "Two",
3: "Three",
4: "Four",
5: "Five",
6: "Six",
7: "Seven",
8: "Eight",
9: "Nine"}
sentences = []
# Create two kinds of sentences - sequences of odd and even digits.
for i in range(10000):
rand_odd_ints = np.random.choice(range(1, 10, 2), 3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_odd_ints]))
rand_even_ints = np.random.choice(range(2, 10, 2), 3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_even_ints]))
# Map words to indices
word2index_map = {}
index = 0
for sent in sentences:
for word in sent.lower().split():
if word not in word2index_map:
word2index_map[word] = index
index += 1
index2word_map = {index: word for word, index in word2index_map.items()}
vocabulary_size = len(index2word_map)
# Generate skip-gram pairs
skip_gram_pairs = []
for sent in sentences:
tokenized_sent = sent.lower().split()
for i in range(1, len(tokenized_sent)-1):
word_context_pair = [[word2index_map[tokenized_sent[i-1]],
word2index_map[tokenized_sent[i+1]]], word2index_map[tokenized_sent[i]]]
skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][0]])
skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][1]])
def get_skipgram_batch(batch_size):
instance_indices = list(range(len(skip_gram_pairs)))
np.random.shuffle(instance_indices)
batch = instance_indices[:batch_size]
x = [skip_gram_pairs[i][0] for i in batch]
y = [[skip_gram_pairs[i][1]] for i in batch]
return x, y
# batch example
x_batch, y_batch = get_skipgram_batch(8)
x_batch
y_batch
[index2word_map[word] for word in x_batch] [index2word_map[word[0]] for word in y_batch]
# Input data, labels train_inputs = tf.placeholder(tf.int32, shape = [batch_size])
train_labels = tf.placeholder(tf.int32, shape = [batch_size, 1])
# Embedding lookup table currently only implemented in CPU with
tf.name_scope("embeddings"):
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_dimension], -1.0, 1.0),
name = 'embedding')
# This is essentialy a lookup table
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
# Create variables for the NCE loss
nce_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_dimension], stddev = 1.0 /
math.sqrt(embedding_dimension)))
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))
loss = tf.reduce_mean(
tf.nn.nce_loss(weights = nce_weights, biases = nce_biases, inputs = embed,
labels = train_labels,num_sampled = negative_samples,
num_classes = vocabulary_size)) tf.summary.scalar("NCE_loss", loss)
# Learning rate decay
global_step = tf.Variable(0, trainable = False)
learningRate = tf.train.exponential_decay(learning_rate = 0.1,
global_step = global_step, decay_steps = 1000, decay_rate = 0.95, staircase = True)
train_step = tf.train.GradientDescentOptimizer(learningRate).minimize(loss)
merged = tf.summary.merge_all()
with tf.Session() as sess:
train_writer = tf.summary.FileWriter(LOG_DIR,
graph = tf.get_default_graph())
saver = tf.train.Saver()
with open(os.path.join(LOG_DIR, 'metadata.tsv'), "w") as metadata:
metadata.write('Name\tClass\n') for k, v in index2word_map.items():
metadata.write('%s\t%d\n' % (v, k))
config = projector.ProjectorConfig()
embedding = config.embeddings.add() embedding.tensor_name = embeddings.name
# Link this tensor to its metadata file (e.g. labels).
embedding.metadata_path = os.path.join(LOG_DIR, 'metadata.tsv')
projector.visualize_embeddings(train_writer, config)
tf.global_variables_initializer().run()
for step in range(1000):
x_batch, y_batch = get_skipgram_batch(batch_size) summary, _ = sess.run(
[merged, train_step], feed_dict = {train_inputs: x_batch, train_labels: y_batch})
train_writer.add_summary(summary, step)
if step % 100 == 0:
saver.save(sess, os.path.join(LOG_DIR, "w2v_model.ckpt"), step)
loss_value = sess.run(loss, feed_dict = {
train_inputs: x_batch, train_labels: y_batch})
print("Loss at %d: %.5f" % (step, loss_value))
# Normalize embeddings before using
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims = True))
normalized_embeddings = embeddings /
norm normalized_embeddings_matrix = sess.run(normalized_embeddings)
ref_word = normalized_embeddings_matrix[word2index_map["one"]]
cosine_dists = np.dot(normalized_embeddings_matrix, ref_word)
ff = np.argsort(cosine_dists)[::-1][1:10] for f in ff: print(index2word_map[f])
print(cosine_dists[f])
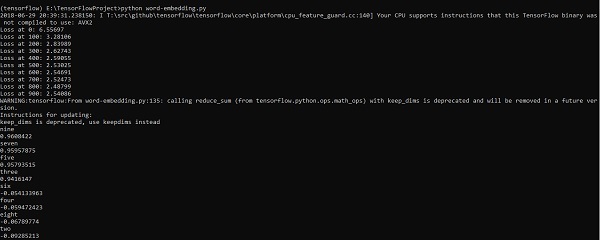
输出
以上代码生成以下输出:
TensorFlow - 单层感知器
为了理解单层感知器,了解人工神经网络 (ANN) 非常重要。人工神经网络是一种信息处理系统,其机制受到生物神经回路功能的启发。人工神经网络拥有许多相互连接的处理单元。以下是人工神经网络的示意图:
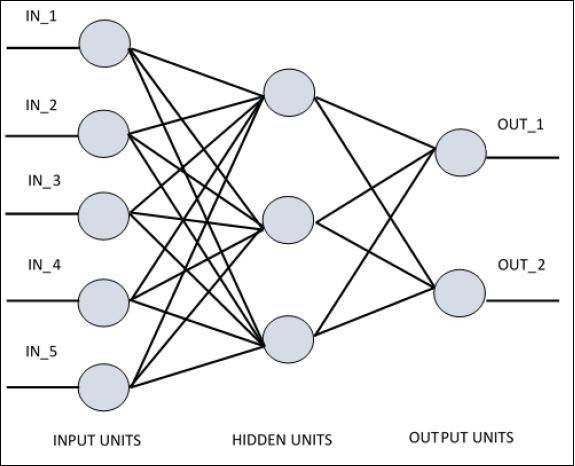
该图显示隐藏单元与外部层通信。而输入和输出单元仅通过网络的隐藏层进行通信。
节点的连接模式、层的总数和输入与输出之间节点的级别以及每层的神经元数量定义了神经网络的架构。
有两种架构类型。这些类型侧重于人工神经网络的功能,如下所示:
- 单层感知器
- 多层感知器
单层感知器
单层感知器是第一个提出的神经模型。神经元的本地存储器的内容包含一个权重向量。单层感知器的计算是在输入向量之和上执行的,每个输入向量都乘以权重向量的对应元素。输出中显示的值将成为激活函数的输入。
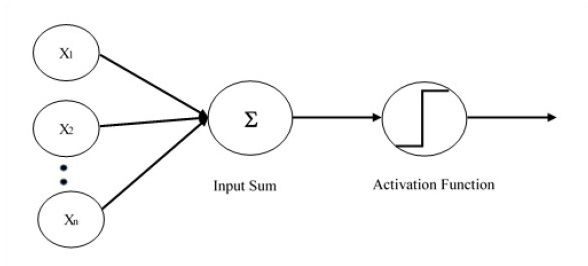
让我们重点关注使用 TensorFlow 对图像分类问题实现单层感知器。通过“逻辑回归”的表示来说明单层感知器的最佳示例。
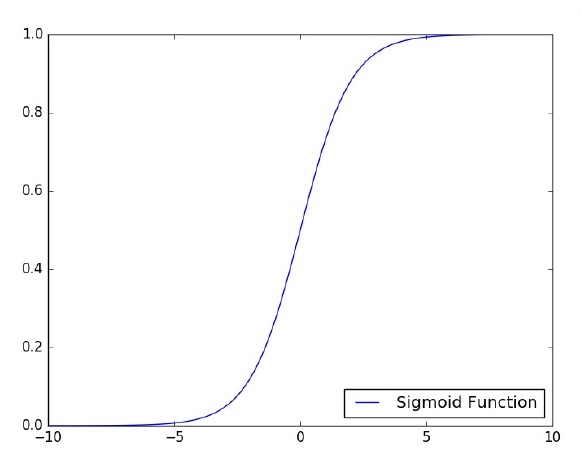
现在,让我们考虑训练逻辑回归的基本步骤:
在训练开始时,权重以随机值初始化。
对于训练集中的每个元素,都计算误差,误差是期望输出与实际输出之间的差异。计算出的误差用于调整权重。
重复此过程,直到整个训练集上的误差不大于指定的阈值,或者达到最大迭代次数。
下面提到了用于评估逻辑回归的完整代码:
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1
# tf Graph Input
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes
# Create model
# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# Construct model
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
# Minimize error using cross entropy
cross_entropy = y*tf.log(activation)
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1))
optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost)
#Plot settings
avg_set = []
epoch_set = []
# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, \ feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
x: batch_xs, \ y: batch_ys})/total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
avg_set.append(avg_cost) epoch_set.append(epoch+1)
print ("Training phase finished")
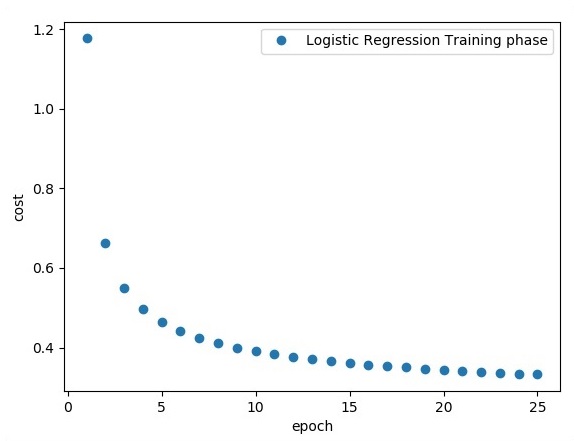
plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print
("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))
输出
以上代码生成以下输出:
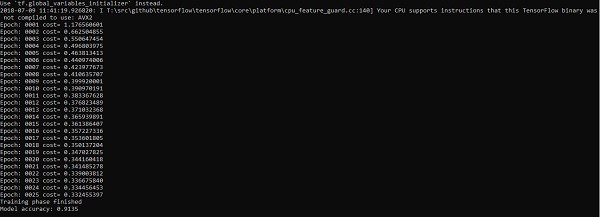
逻辑回归被认为是一种预测分析。逻辑回归用于描述数据并解释一个二元因变量与一个或多个名义或自变量之间的关系。
TensorFlow - 线性回归
在本章中,我们将重点关注使用 TensorFlow 实现线性回归的基本示例。逻辑回归或线性回归是一种监督机器学习方法,用于对有序离散类别进行分类。我们本章的目标是构建一个模型,用户可以通过该模型预测预测变量与一个或多个自变量之间的关系。
这两个变量之间的关系被认为是线性的。如果 y 是因变量,x 被认为是自变量,那么这两个变量的线性回归关系将如下所示:
Y = Ax+b
我们将设计一种线性回归算法。这将使我们能够理解以下两个重要概念:
- 成本函数
- 梯度下降算法
线性回归的示意图如下所示:

线性回归方程的图形视图如下所示:
设计线性回归算法的步骤
我们现在将学习有助于设计线性回归算法的步骤。
步骤 1
导入绘制线性回归模块所需的必要模块非常重要。我们首先导入 Python 库 NumPy 和 Matplotlib。
import numpy as np import matplotlib.pyplot as plt
步骤 2
定义逻辑回归所需的系数数量。
number_of_points = 500 x_point = [] y_point = [] a = 0.22 b = 0.78
步骤 3
迭代变量以生成回归方程周围的 300 个随机点:
Y = 0.22x+0.78
for i in range(number_of_points): x = np.random.normal(0.0,0.5) y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) y_point.append([y])
步骤 4
使用 Matplotlib 查看生成的点。
fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()
逻辑回归的完整代码如下所示:
import numpy as np import matplotlib.pyplot as plt number_of_points = 500 x_point = [] y_point = [] a = 0.22 b = 0.78 for i in range(number_of_points): x = np.random.normal(0.0,0.5) y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) y_point.append([y]) plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()
作为输入获取的点数被视为输入数据。
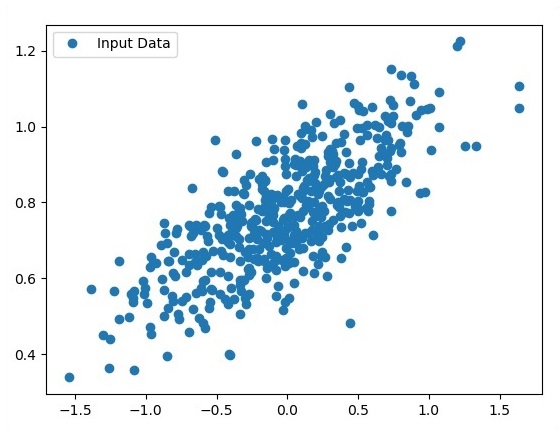
TensorFlow - TFLearn 及其安装
TFLearn 可以定义为 TensorFlow 框架中使用的模块化且透明的深度学习方面。TFLearn 的主要动机是为 TensorFlow 提供更高级别的 API,以促进和展示新的实验。
考虑以下 TFLearn 的重要功能:
TFLearn 易于使用和理解。
它包括易于构建高度模块化网络层、优化器和嵌入其中的各种指标的概念。
它包括与 TensorFlow 工作系统的完全透明性。
它包括强大的辅助函数来训练内置张量,这些张量接受多个输入、输出和优化器。
它包括简单而漂亮的图形可视化。
图形可视化包括权重、梯度和激活的各种详细信息。
通过执行以下命令安装 TFLearn:
pip install tflearn
执行上述代码后,将生成以下输出:
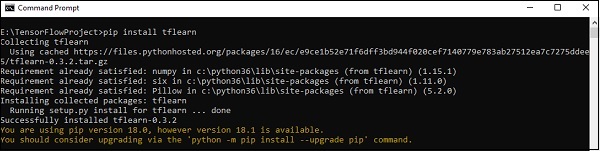
以下插图显示了使用随机森林分类器实现 TFLearn:
from __future__ import division, print_function, absolute_import
#TFLearn module implementation
import tflearn
from tflearn.estimators import RandomForestClassifier
# Data loading and pre-processing with respect to dataset
import tflearn.datasets.mnist as mnist
X, Y, testX, testY = mnist.load_data(one_hot = False)
m = RandomForestClassifier(n_estimators = 100, max_nodes = 1000)
m.fit(X, Y, batch_size = 10000, display_step = 10)
print("Compute the accuracy on train data:")
print(m.evaluate(X, Y, tflearn.accuracy_op))
print("Compute the accuracy on test set:")
print(m.evaluate(testX, testY, tflearn.accuracy_op))
print("Digits for test images id 0 to 5:")
print(m.predict(testX[:5]))
print("True digits:")
print(testY[:5])
TensorFlow - CNN 和 RNN 的区别
在本章中,我们将重点关注 CNN 和 RNN 之间的区别:
| CNN | RNN |
|---|---|
| 它适用于空间数据,例如图像。 | RNN 适用于时间数据,也称为顺序数据。 |
| CNN 被认为比 RNN 更强大。 | 与 CNN 相比,RNN 的功能兼容性较差。 |
| 此网络采用固定大小的输入并生成固定大小的输出。 | RNN 可以处理任意输入/输出长度。 |
| CNN 是一种前馈人工神经网络,具有多层感知器的变体,旨在使用最少的预处理量。 | 与前馈神经网络不同,RNN 可以利用其内部记忆来处理任意输入序列。 |
| CNN 利用神经元之间的连接模式。这受到动物视觉皮层的组织结构的启发,动物视觉皮层的单个神经元以某种方式排列,以便对视觉场的重叠区域做出反应。 | 循环神经网络使用时间序列信息 - 用户上次说了什么会影响他/她接下来会说什么。 |
| CNN 非常适合图像和视频处理。 | RNN 非常适合文本和语音分析。 |
下图显示了 CNN 和 RNN 的示意图 -
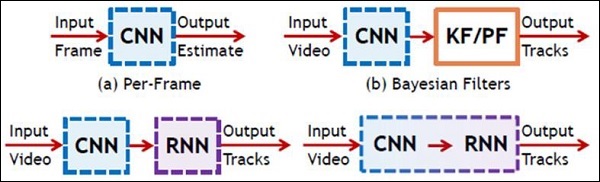
TensorFlow - Keras
Keras 是一个紧凑、易于学习的高级 Python 库,运行在 TensorFlow 框架之上。它专注于理解深度学习技术,例如为神经网络创建层,同时保持形状和数学细节的概念。框架的创建可以分为以下两种类型 -
- 顺序 API
- 函数式 API
考虑以下八个步骤在 Keras 中创建深度学习模型 -
- 加载数据
- 预处理加载的数据
- 模型定义
- 编译模型
- 拟合指定的模型
- 评估模型
- 做出所需的预测
- 保存模型
我们将使用 Jupyter Notebook 来执行和显示输出,如下所示 -
步骤 1 - 首先加载数据并预处理加载的数据,以执行深度学习模型。
import warnings
warnings.filterwarnings('ignore')
import numpy as np
np.random.seed(123) # for reproducibility
from keras.models import Sequential
from keras.layers import Flatten, MaxPool2D, Conv2D, Dense, Reshape, Dropout
from keras.utils import np_utils
Using TensorFlow backend.
from keras.datasets import mnist
# Load pre-shuffled MNIST data into train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)
此步骤可以定义为“导入库和模块”,这意味着所有库和模块都作为初始步骤导入。
步骤 2 - 在此步骤中,我们将定义模型架构 -
model = Sequential() model.add(Conv2D(32, 3, 3, activation = 'relu', input_shape = (28,28,1))) model.add(Conv2D(32, 3, 3, activation = 'relu')) model.add(MaxPool2D(pool_size = (2,2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(128, activation = 'relu')) model.add(Dropout(0.5)) model.add(Dense(10, activation = 'softmax'))
步骤 3 - 现在让我们编译指定的模型 -
model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
步骤 4 - 我们现在将使用训练数据拟合模型 -
model.fit(X_train, Y_train, batch_size = 32, epochs = 10, verbose = 1)
创建的迭代输出如下 -
Epoch 1/10 60000/60000 [==============================] - 65s - loss: 0.2124 - acc: 0.9345 Epoch 2/10 60000/60000 [==============================] - 62s - loss: 0.0893 - acc: 0.9740 Epoch 3/10 60000/60000 [==============================] - 58s - loss: 0.0665 - acc: 0.9802 Epoch 4/10 60000/60000 [==============================] - 62s - loss: 0.0571 - acc: 0.9830 Epoch 5/10 60000/60000 [==============================] - 62s - loss: 0.0474 - acc: 0.9855 Epoch 6/10 60000/60000 [==============================] - 59s - loss: 0.0416 - acc: 0.9871 Epoch 7/10 60000/60000 [==============================] - 61s - loss: 0.0380 - acc: 0.9877 Epoch 8/10 60000/60000 [==============================] - 63s - loss: 0.0333 - acc: 0.9895 Epoch 9/10 60000/60000 [==============================] - 64s - loss: 0.0325 - acc: 0.9898 Epoch 10/10 60000/60000 [==============================] - 60s - loss: 0.0284 - acc: 0.9910
TensorFlow - 分布式计算
本章将重点介绍如何开始使用分布式 TensorFlow。目的是帮助开发人员理解反复出现的分布式 TF 基本概念,例如 TF 服务器。我们将使用 Jupyter Notebook 来评估分布式 TensorFlow。TensorFlow 的分布式计算实现如下 -
步骤 1 - 导入分布式计算所需的必要模块 -
import tensorflow as tf
步骤 2 - 创建一个具有一个节点的 TensorFlow 集群。让此节点负责一个名为“worker”的任务,该任务将在 localhost:2222 上运行一个操作。
cluster_spec = tf.train.ClusterSpec({'worker' : ['localhost:2222']})
server = tf.train.Server(cluster_spec)
server.target
以上脚本生成以下输出 -
'grpc://:2222' The server is currently running.
步骤 3 - 可以通过执行以下命令来计算相应的会话的服务器配置 -
server.server_def
以上命令生成以下输出 -
cluster {
job {
name: "worker"
tasks {
value: "localhost:2222"
}
}
}
job_name: "worker"
protocol: "grpc"
步骤 4 - 启动一个 TensorFlow 会话,其执行引擎为服务器。使用 TensorFlow 创建一个本地服务器,并使用lsof找出服务器的位置。
sess = tf.Session(target = server.target) server = tf.train.Server.create_local_server()
步骤 5 - 查看此会话中可用的设备,并关闭相应的会话。
devices = sess.list_devices() for d in devices: print(d.name) sess.close()
以上命令生成以下输出 -
/job:worker/replica:0/task:0/device:CPU:0
TensorFlow - 导出
在这里,我们将重点关注 TensorFlow 中的 MetaGraph 形成。这将有助于我们理解 TensorFlow 中的导出模块。MetaGraph 包含基本信息,这些信息是训练、执行评估或在先前训练的图上运行推理所必需的。
以下是相同的代码片段 -
def export_meta_graph(filename = None, collection_list = None, as_text = False):
"""this code writes `MetaGraphDef` to save_path/filename.
Arguments:
filename: Optional meta_graph filename including the path. collection_list:
List of string keys to collect. as_text: If `True`,
writes the meta_graph as an ASCII proto.
Returns:
A `MetaGraphDef` proto. """
下面提到了一个典型的用法模型 -
# Build the model ... with tf.Session() as sess: # Use the model ... # Export the model to /tmp/my-model.meta. meta_graph_def = tf.train.export_meta_graph(filename = '/tmp/my-model.meta')
TensorFlow - 多层感知器学习
多层感知器定义了人工神经网络中最复杂的架构。它基本上由多层感知器组成。
多层感知器学习的图示如下所示 -
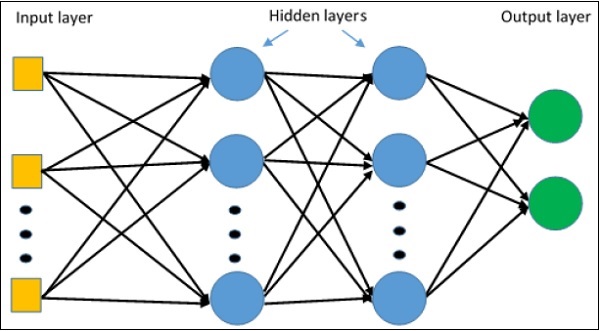
MLP 网络通常用于监督学习格式。MLP 网络的典型学习算法也称为反向传播算法。
现在,我们将重点关注使用 MLP 解决图像分类问题的实现。
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.001
training_epochs = 20
batch_size = 100
display_step = 1
# Network Parameters
n_hidden_1 = 256
# 1st layer num features
n_hidden_2 = 256 # 2nd layer num features
n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10
# MNIST total classes (0-9 digits)
# tf Graph input
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])
# weights layer 1
h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) # bias layer 1
bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1]))
# layer 1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, h), bias_layer_1))
# weights layer 2
w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2]))
# bias layer 2
bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2]))
# layer 2
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w), bias_layer_2))
# weights output layer
output = tf.Variable(tf.random_normal([n_hidden_2, n_classes]))
# biar output layer
bias_output = tf.Variable(tf.random_normal([n_classes])) # output layer
output_layer = tf.matmul(layer_2, output) + bias_output
# cost function
cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits = output_layer, labels = y))
#cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(output_layer, y))
# optimizer
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
# optimizer = tf.train.GradientDescentOptimizer(
learning_rate = learning_rate).minimize(cost)
# Plot settings
avg_set = []
epoch_set = []
# Initializing the variables
init = tf.global_variables_initializer()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples / batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss
avg_cost += sess.run(cost, feed_dict = {x: batch_xs, y: batch_ys}) / total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print
Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(avg_cost)
avg_set.append(avg_cost)
epoch_set.append(epoch + 1)
print
"Training phase finished"
plt.plot(epoch_set, avg_set, 'o', label = 'MLP Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(output_layer, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print
"Model Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})
以上代码行生成以下输出 -
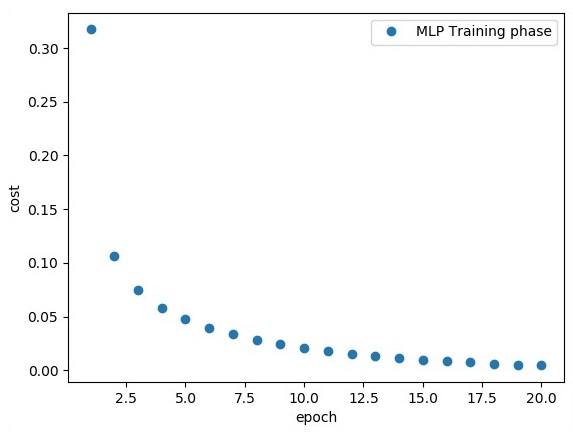
TensorFlow - 感知器的隐藏层
在本章中,我们将重点关注我们必须从称为 x 和 f(x) 的已知点集中学习的网络。一个隐藏层将构建这个简单的网络。
感知器隐藏层解释的代码如下所示 -
#Importing the necessary modules
import tensorflow as tf
import numpy as np
import math, random
import matplotlib.pyplot as plt
np.random.seed(1000)
function_to_learn = lambda x: np.cos(x) + 0.1*np.random.randn(*x.shape)
layer_1_neurons = 10
NUM_points = 1000
#Training the parameters
batch_size = 100
NUM_EPOCHS = 1500
all_x = np.float32(np.random.uniform(-2*math.pi, 2*math.pi, (1, NUM_points))).T
np.random.shuffle(all_x)
train_size = int(900)
#Training the first 700 points in the given set x_training = all_x[:train_size]
y_training = function_to_learn(x_training)
#Training the last 300 points in the given set x_validation = all_x[train_size:]
y_validation = function_to_learn(x_validation)
plt.figure(1)
plt.scatter(x_training, y_training, c = 'blue', label = 'train')
plt.scatter(x_validation, y_validation, c = 'pink', label = 'validation')
plt.legend()
plt.show()
X = tf.placeholder(tf.float32, [None, 1], name = "X")
Y = tf.placeholder(tf.float32, [None, 1], name = "Y")
#first layer
#Number of neurons = 10
w_h = tf.Variable(
tf.random_uniform([1, layer_1_neurons],\ minval = -1, maxval = 1, dtype = tf.float32))
b_h = tf.Variable(tf.zeros([1, layer_1_neurons], dtype = tf.float32))
h = tf.nn.sigmoid(tf.matmul(X, w_h) + b_h)
#output layer
#Number of neurons = 10
w_o = tf.Variable(
tf.random_uniform([layer_1_neurons, 1],\ minval = -1, maxval = 1, dtype = tf.float32))
b_o = tf.Variable(tf.zeros([1, 1], dtype = tf.float32))
#build the model
model = tf.matmul(h, w_o) + b_o
#minimize the cost function (model - Y)
train_op = tf.train.AdamOptimizer().minimize(tf.nn.l2_loss(model - Y))
#Start the Learning phase
sess = tf.Session() sess.run(tf.initialize_all_variables())
errors = []
for i in range(NUM_EPOCHS):
for start, end in zip(range(0, len(x_training), batch_size),\
range(batch_size, len(x_training), batch_size)):
sess.run(train_op, feed_dict = {X: x_training[start:end],\ Y: y_training[start:end]})
cost = sess.run(tf.nn.l2_loss(model - y_validation),\ feed_dict = {X:x_validation})
errors.append(cost)
if i%100 == 0:
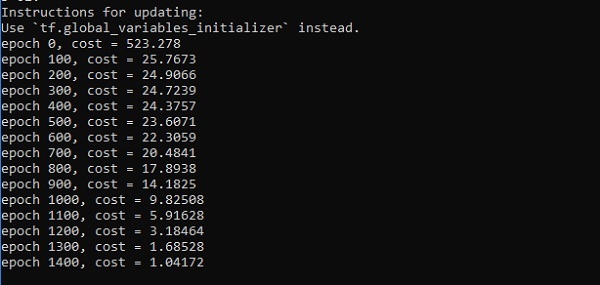
print("epoch %d, cost = %g" % (i, cost))
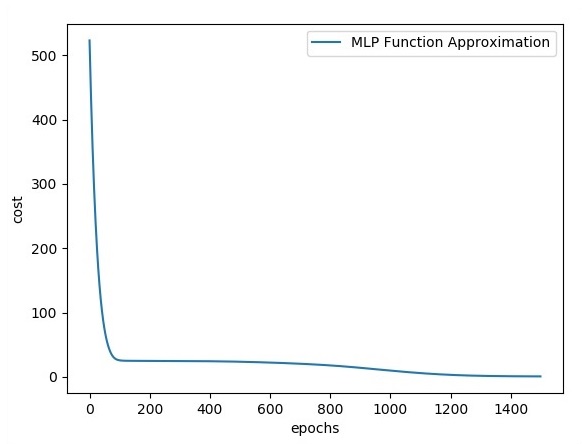
plt.plot(errors,label='MLP Function Approximation') plt.xlabel('epochs')
plt.ylabel('cost')
plt.legend()
plt.show()
输出
以下是函数层近似的表示 -
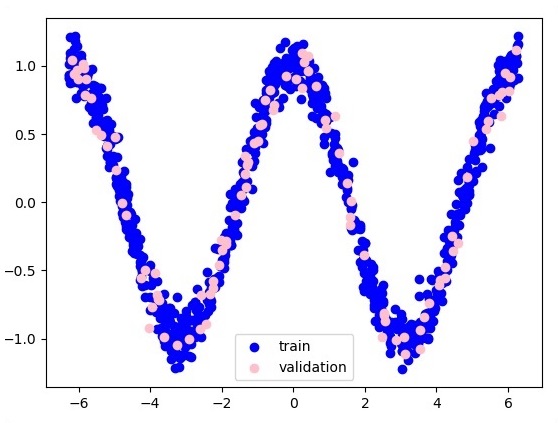
这里两个数据以 W 的形状表示。这两个数据是:训练和验证,它们以不同的颜色表示,如图例部分所示。
TensorFlow - 优化器
优化器是扩展类,其中包含用于训练特定模型的附加信息。优化器类使用给定参数进行初始化,但重要的是要记住不需要张量。优化器用于提高训练特定模型的速度和性能。
TensorFlow 的基本优化器是 -
tf.train.Optimizer
此类在 tensorflow/python/training/optimizer.py 的指定路径中定义。
以下是 TensorFlow 中的一些优化器 -
- 随机梯度下降
- 带有梯度裁剪的随机梯度下降
- 动量
- Nesterov 动量
- Adagrad
- Adadelta
- RMSProp
- Adam
- Adamax
- SMORMS3
我们将重点关注随机梯度下降。为其创建优化器的图示如下所示 -
def sgd(cost, params, lr = np.float32(0.01)):
g_params = tf.gradients(cost, params)
updates = []
for param, g_param in zip(params, g_params):
updates.append(param.assign(param - lr*g_param))
return updates
基本参数在特定函数内定义。在我们接下来的章节中,我们将重点关注梯度下降优化以及优化器的实现。
TensorFlow - XOR 实现
在本章中,我们将学习有关使用 TensorFlow 实现 XOR 的知识。在开始使用 TensorFlow 实现 XOR 之前,让我们看看 XOR 表的值。这将帮助我们理解加密和解密过程。
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR 密码加密方法基本上用于加密难以用蛮力方法破解的数据,即通过生成与适当密钥匹配的随机加密密钥。
使用 XOR 密码进行实现的概念是定义一个 XOR 加密密钥,然后使用此密钥对指定字符串中的字符执行 XOR 操作,用户尝试使用此密钥加密数据。现在我们将重点介绍使用 TensorFlow 实现 XOR,如下所示 -
#Declaring necessary modules
import tensorflow as tf
import numpy as np
"""
A simple numpy implementation of a XOR gate to understand the backpropagation
algorithm
"""
x = tf.placeholder(tf.float64,shape = [4,2],name = "x")
#declaring a place holder for input x
y = tf.placeholder(tf.float64,shape = [4,1],name = "y")
#declaring a place holder for desired output y
m = np.shape(x)[0]#number of training examples
n = np.shape(x)[1]#number of features
hidden_s = 2 #number of nodes in the hidden layer
l_r = 1#learning rate initialization
theta1 = tf.cast(tf.Variable(tf.random_normal([3,hidden_s]),name = "theta1"),tf.float64)
theta2 = tf.cast(tf.Variable(tf.random_normal([hidden_s+1,1]),name = "theta2"),tf.float64)
#conducting forward propagation
a1 = tf.concat([np.c_[np.ones(x.shape[0])],x],1)
#the weights of the first layer are multiplied by the input of the first layer
z1 = tf.matmul(a1,theta1)
#the input of the second layer is the output of the first layer, passed through the
activation function and column of biases is added
a2 = tf.concat([np.c_[np.ones(x.shape[0])],tf.sigmoid(z1)],1)
#the input of the second layer is multiplied by the weights
z3 = tf.matmul(a2,theta2)
#the output is passed through the activation function to obtain the final probability
h3 = tf.sigmoid(z3)
cost_func = -tf.reduce_sum(y*tf.log(h3)+(1-y)*tf.log(1-h3),axis = 1)
#built in tensorflow optimizer that conducts gradient descent using specified
learning rate to obtain theta values
optimiser = tf.train.GradientDescentOptimizer(learning_rate = l_r).minimize(cost_func)
#setting required X and Y values to perform XOR operation
X = [[0,0],[0,1],[1,0],[1,1]]
Y = [[0],[1],[1],[0]]
#initializing all variables, creating a session and running a tensorflow session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
#running gradient descent for each iteration and printing the hypothesis
obtained using the updated theta values
for i in range(100000):
sess.run(optimiser, feed_dict = {x:X,y:Y})#setting place holder values using feed_dict
if i%100==0:
print("Epoch:",i)
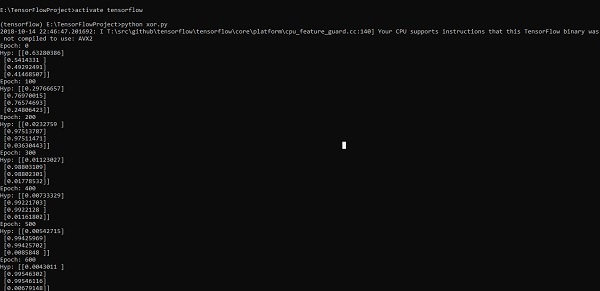
print("Hyp:",sess.run(h3,feed_dict = {x:X,y:Y}))
以上代码行生成如下截图所示的输出 -
TensorFlow - 梯度下降优化
梯度下降优化被认为是数据科学中的一个重要概念。
考虑以下步骤以了解梯度下降优化的实现 -
步骤 1
包含必要的模块并通过我们将要定义梯度下降优化的 x 和 y 变量进行声明。
import tensorflow as tf x = tf.Variable(2, name = 'x', dtype = tf.float32) log_x = tf.log(x) log_x_squared = tf.square(log_x) optimizer = tf.train.GradientDescentOptimizer(0.5) train = optimizer.minimize(log_x_squared)
步骤 2
初始化必要的变量并调用优化器以定义并使用相应的函数调用它。
init = tf.initialize_all_variables()
def optimize():
with tf.Session() as session:
session.run(init)
print("starting at", "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
for step in range(10):
session.run(train)
print("step", step, "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
optimize()
以上代码行生成如下截图所示的输出 -
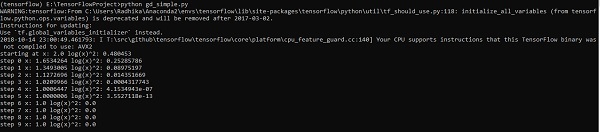
我们可以看到必要的 epoch 和迭代次数已如输出所示计算出来。
TensorFlow - 构建图
偏微分方程 (PDE) 是一种微分方程,它涉及具有多个自变量的未知函数的偏导数。关于偏微分方程,我们将重点关注创建新的图形。
让我们假设有一个尺寸为 500*500 平方英尺的水池 -
N = 500
现在,我们将计算偏微分方程并使用它形成相应的图形。考虑以下步骤以计算图形。
步骤 1 - 导入用于仿真的库。
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt
步骤 2 - 包含将 2D 数组转换为卷积核和简化的 2D 卷积运算的函数。
def make_kernel(a): a = np.asarray(a) a = a.reshape(list(a.shape) + [1,1]) return tf.constant(a, dtype=1) def simple_conv(x, k): """A simplified 2D convolution operation""" x = tf.expand_dims(tf.expand_dims(x, 0), -1) y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME') return y[0, :, :, 0] def laplace(x): """Compute the 2D laplacian of an array""" laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]]) return simple_conv(x, laplace_k) sess = tf.InteractiveSession()
步骤 3 - 包含迭代次数并计算图形以相应地显示记录。
N = 500
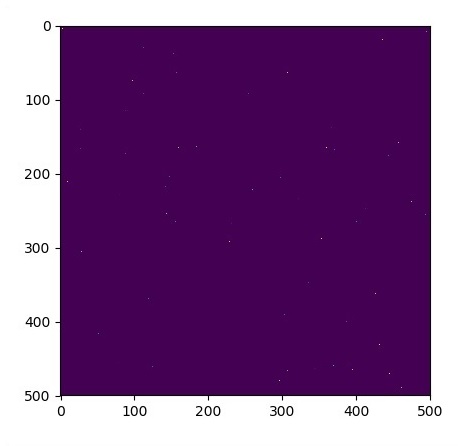
# Initial Conditions -- some rain drops hit a pond
# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)
# Some rain drops hit a pond at random points
for n in range(100):
a,b = np.random.randint(0, N, 2)
u_init[a,b] = np.random.uniform()
plt.imshow(u_init)
plt.show()
# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())
# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)
# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)
# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))
# Initialize state to initial conditions
tf.initialize_all_variables().run()
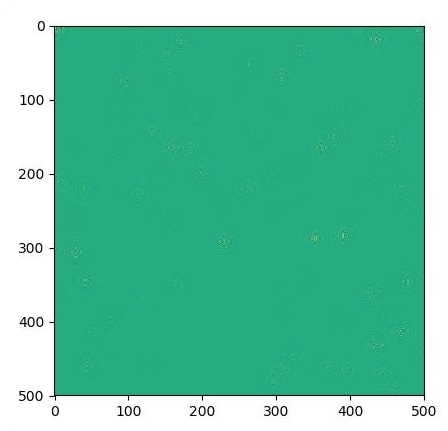
# Run 1000 steps of PDE
for i in range(1000):
# Step simulation
step.run({eps: 0.03, damping: 0.04})
# Visualize every 50 steps
if i % 500 == 0:
plt.imshow(U.eval())
plt.show()
图形绘制如下所示 -
使用 TensorFlow 进行图像识别
TensorFlow 包含一个特殊的图像识别功能,这些图像存储在特定文件夹中。对于相对相同的图像,将很容易为安全目的实现此逻辑。
图像识别代码实现的文件夹结构如下所示 -
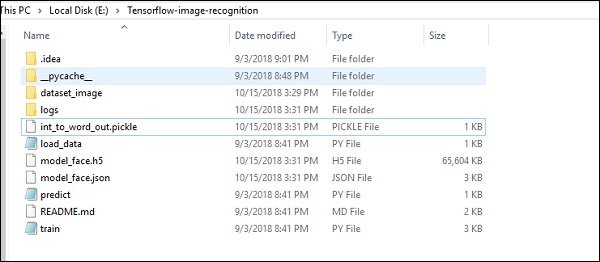
dataset_image 包含需要加载的相关图像。我们将重点关注使用我们定义的徽标进行图像识别。图像使用“load_data.py”脚本加载,这有助于记录其中的各种图像识别模块。
import pickle
from sklearn.model_selection import train_test_split
from scipy import misc
import numpy as np
import os
label = os.listdir("dataset_image")
label = label[1:]
dataset = []
for image_label in label:
images = os.listdir("dataset_image/"+image_label)
for image in images:
img = misc.imread("dataset_image/"+image_label+"/"+image)
img = misc.imresize(img, (64, 64))
dataset.append((img,image_label))
X = []
Y = []
for input,image_label in dataset:
X.append(input)
Y.append(label.index(image_label))
X = np.array(X)
Y = np.array(Y)
X_train,y_train, = X,Y
data_set = (X_train,y_train)
save_label = open("int_to_word_out.pickle","wb")
pickle.dump(label, save_label)
save_label.close()
图像的训练有助于将可识别的模式存储在指定的文件夹中。
import numpy
import matplotlib.pyplot as plt
from keras.layers import Dropout
from keras.layers import Flatten
from keras.constraints import maxnorm
from keras.optimizers import SGD
from keras.layers import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.utils import np_utils
from keras import backend as K
import load_data
from keras.models import Sequential
from keras.layers import Dense
import keras
K.set_image_dim_ordering('tf')
# fix random seed for reproducibility
seed = 7
numpy.random.seed(seed)
# load data
(X_train,y_train) = load_data.data_set
# normalize inputs from 0-255 to 0.0-1.0
X_train = X_train.astype('float32')
#X_test = X_test.astype('float32')
X_train = X_train / 255.0
#X_test = X_test / 255.0
# one hot encode outputs
y_train = np_utils.to_categorical(y_train)
#y_test = np_utils.to_categorical(y_test)
num_classes = y_train.shape[1]
# Create the model
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape = (64, 64, 3), padding = 'same',
activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.2))
model.add(Conv2D(32, (3, 3), activation = 'relu', padding = 'same',
kernel_constraint = maxnorm(3)))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Flatten())
model.add(Dense(512, activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation = 'softmax'))
# Compile model
epochs = 10
lrate = 0.01
decay = lrate/epochs
sgd = SGD(lr = lrate, momentum = 0.9, decay = decay, nesterov = False)
model.compile(loss = 'categorical_crossentropy', optimizer = sgd, metrics = ['accuracy'])
print(model.summary())
#callbacks = [keras.callbacks.EarlyStopping(
monitor = 'val_loss', min_delta = 0, patience = 0, verbose = 0, mode = 'auto')]
callbacks = [keras.callbacks.TensorBoard(log_dir='./logs',
histogram_freq = 0, batch_size = 32, write_graph = True, write_grads = False,
write_images = True, embeddings_freq = 0, embeddings_layer_names = None,
embeddings_metadata = None)]
# Fit the model
model.fit(X_train, y_train, epochs = epochs,
batch_size = 32,shuffle = True,callbacks = callbacks)
# Final evaluation of the model
scores = model.evaluate(X_train, y_train, verbose = 0)
print("Accuracy: %.2f%%" % (scores[1]*100))
# serialize model to JSONx
model_json = model.to_json()
with open("model_face.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights("model_face.h5")
print("Saved model to disk")
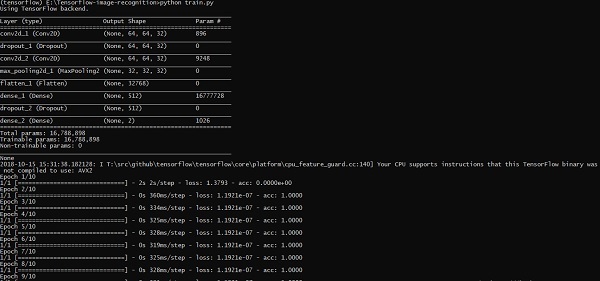
以上代码行生成如下所示的输出 -
神经网络训练建议
在本章中,我们将了解可以使用 TensorFlow 框架实现的神经网络训练的各个方面。
以下是可以评估的十项建议 -
反向传播
反向传播是一种计算偏导数的简单方法,它包括最适合神经网络的基本合成形式。
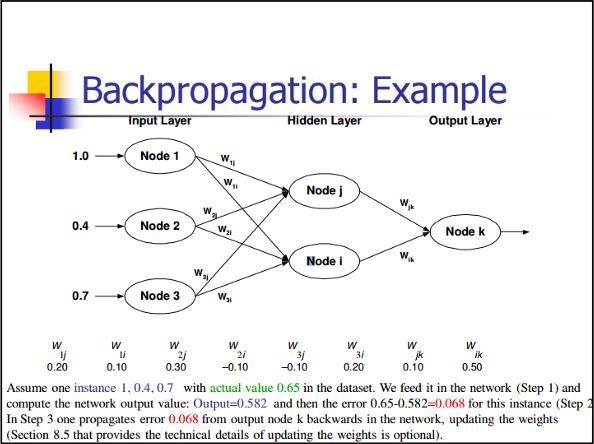
随机梯度下降
在随机梯度下降中,**批次**是用户在单个迭代中用于计算梯度的示例总数。到目前为止,假设批次已成为整个数据集。最好的说明是在 Google 规模下工作;数据集通常包含数十亿甚至数百亿个示例。
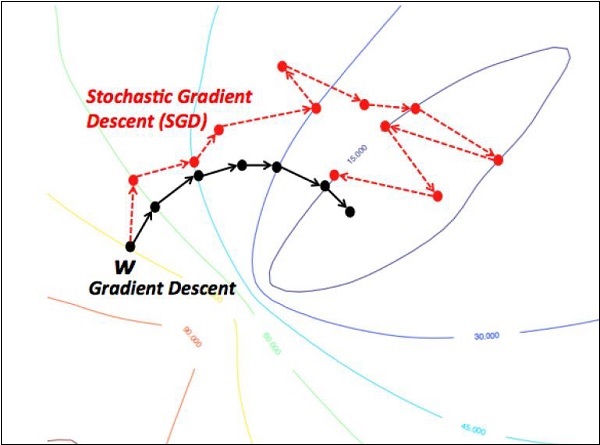
学习率衰减
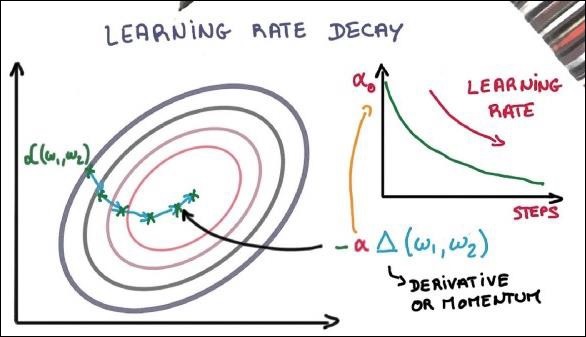
调整学习率是梯度下降优化最重要的功能之一。这对 TensorFlow 实现至关重要。
Dropout
具有大量参数的深度神经网络形成了强大的机器学习系统。但是,过拟合是此类网络中的一个严重问题。
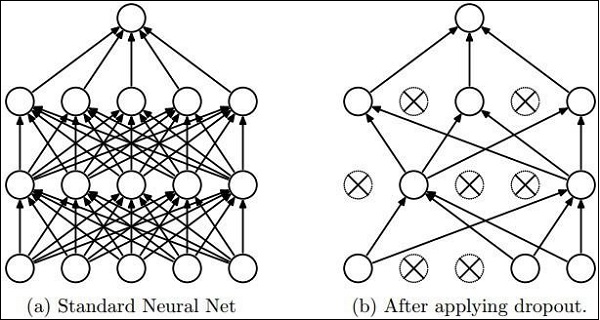
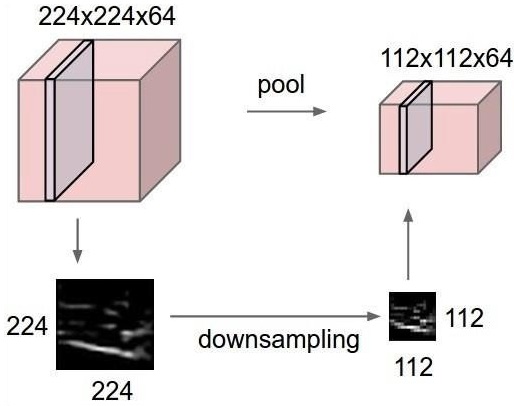
最大池化
最大池化是一个基于样本的离散化过程。目的是对输入表示进行下采样,这在必要的假设下降低了维度。
长短期记忆 (LSTM)
LSTM 控制对在指定神经元中应采用哪些输入的决策。它包括控制决定应该计算什么以及应该生成什么输出。