下表给出了已婚女性按结婚年龄的频数分布

年龄（岁）	频数	年龄（岁）	频数
15-19	53	40-44	9
20-24	140	45-49	5
25-29	98	50-54	3
30-34	32	55-59	3
35-39	12	60岁及以上	2

计算中位数并解释结果。

已知

给定表格给出了已婚女性按结婚年龄的频数分布。

要求

我们必须找到 中位数并解释结果。

解答

将各组以互斥形式排列，然后形成其累积频数表如下，得到，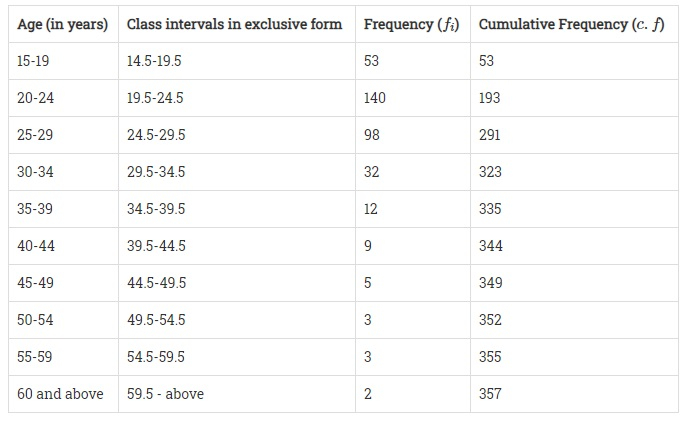

这里，

$N = 357$

$\frac{N}{2} = \frac{357}{2} = 178.5$

刚刚大于 $\frac{N}{2}$ 的累积频数是 193，对应的组是 20 – 24。

这意味着，19.5 – 24.5 是中位数组。

因此，

$l = 19.5, f = 140, F = 53$ 和 $h = (24.5 - 19.5) = 5$

中位数 $=\mathrm{l}+\frac{\frac{\mathrm{N}}{2}-\mathrm{F}}{\mathrm{f}} \times \mathrm{h}$

$=19.5+\frac{178.5-53}{140} \times 5$

$=19.5+\frac{125.5}{140} \times 5$

$=19.5+\frac{125.5}{28}$

$= 19.5 + 4.48$

$= 23.98$

这意味着，近一半的女性在 15 到 24 岁之间结婚。

教程点

更新于： 2022-10-10

57 次查看

开启你的 职业生涯

完成课程获得认证

开始学习