射极跟随器和达林顿放大器

---

---

射极跟随器和达林顿放大器是反馈放大器最常见的例子。它们是最常用的，并且有许多应用。

射极跟随器

射极跟随器电路在反馈放大器中占据着突出的地位。射极跟随器是负电流反馈电路的一种情况。它主要用作信号发生器电路中的最后一级放大器。

射极跟随器的重要特征如下：

• 它具有高输入阻抗
• 它具有低输出阻抗
• 它是阻抗匹配的理想电路

所有这些理想特性都为射极跟随器电路提供了许多应用。这是一个电流放大器电路，没有电压增益。

结构

射极跟随器电路的结构细节与普通放大器几乎相同。主要区别在于负载RL不存在于集电极端，而存在于电路的射极端。因此，输出是从射极端而不是集电极端获取的。

偏置可以通过基极电阻法或分压器法提供。下图显示了射极跟随器的电路图。

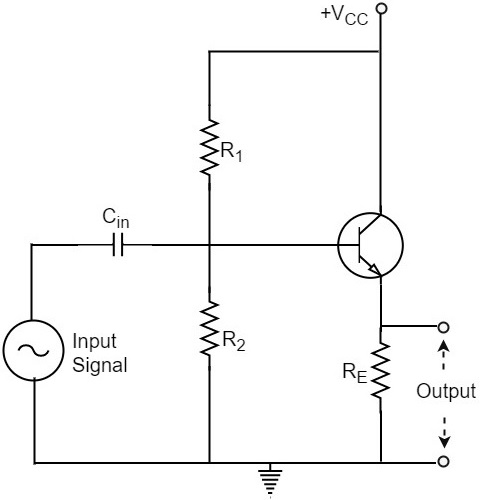
操作

施加在基极和射极之间的输入信号电压在RE上产生输出电压Vo，RE位于射极部分。因此，

$$V_o = I_E R_E$$

整个输出电流通过反馈施加到输入。因此，

$$V_f = V_o$$

由于在RL上产生的输出电压与射极电流成正比，因此该射极跟随器电路是电流反馈电路。因此，

$$\beta = \frac{V_f}{V_o} = 1$$

还注意到，晶体管的输入信号电压（= Vi）等于Vs和Vo的差，即

$$V_i = V_s - V_o$$

因此反馈是负反馈。

特性

射极跟随器的主要特性如下：

• 无电压增益。实际上，电压增益接近1。
• 相对较高的电流增益和功率增益。
• 高输入阻抗和低输出阻抗。
• 输入和输出交流电压同相。

射极跟随器的电压增益

由于射极跟随器电路是一个突出的电路，让我们尝试获得射极跟随器电路的电压增益方程。我们的射极跟随器电路如下所示：

如果绘制上述电路的交流等效电路，它将如下所示，因为射极旁路电容器不存在。

射极电路的交流电阻rE由下式给出

$$r_E = r’_E + R_E$$

其中

$$r’_E = \frac{25 mV}{I_E}$$

为了找到放大器的电压增益，上图可以用下图代替。

请注意，输入电压施加在射极电路的交流电阻上，即（r'E + RE）。假设射极二极管是理想的，输出电压Vout将为

$$V_{out} = i_e R_E$$

输入电压Vin将为

$$V_{in} = i_e(r’_e + R_E)$$

因此，射极跟随器的电压增益为

$$A_V = \frac{V_{out}}{V_{in}} = \frac{i_e R_E}{i_e(r’_e + R_E)} = \frac{R_E}{(r’_e + R_E)}$$

或

$$A_V = \frac{R_E}{(r’_e + R_E)}$$

在大多数实际应用中，

$$R_E \gg r’_e$$

因此，AV ≈ 1。在实践中，射极跟随器的电压增益在0.8到0.999之间。

达林顿放大器

刚刚讨论的射极跟随器电路无法满足电路电流增益（Ai）和输入阻抗（Zi）的要求。为了实现电路电流增益和输入阻抗整体值的增加，两个晶体管连接如下面的电路图所示，这被称为达林顿配置。

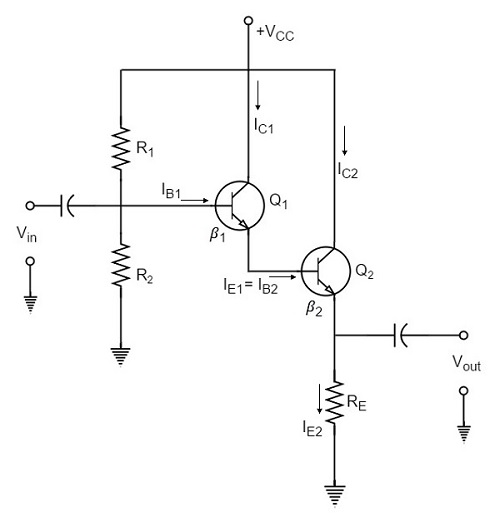
如上图所示，第一个晶体管的射极连接到第二个晶体管的基极。两个晶体管的集电极端连接在一起。

偏置分析

由于这种类型的连接，第一个晶体管的射极电流也将是第二个晶体管的基极电流。因此，对的电流增益等于各个电流增益的乘积，即

$$\beta = \beta _1 \beta _2$$

通常可以通过最少的元件来获得高电流增益。

由于这里使用了两个晶体管，因此需要考虑两个VBE压降。否则，偏置分析与一个晶体管类似。

R2上的电压，

$$V_2 = \frac{V_CC}{R_1 + R_2} \times R_2$$

RE上的电压，

$$V_E = V_2 - 2 V_{BE}$$

通过RE的电流，

$$I_{E2} = \frac{V_2 - 2 V_{BE}}{R_E}$$

由于晶体管是直接耦合的，

$$I_{E1} = I_{B2}$$

现在

$$I_{B2} = \frac{I_{E2}}{\beta _2}$$

因此

$$I_{E1} = \frac{I_{E2}}{\beta _2}$$

这意味着

$$I_{E1} = I_{E1} \beta _2$$

我们有

$I_{E1} = \beta _1 I_{B1}$ 因为 $I_{E1} \cong I_{C1}$

因此，作为

$$I_{E2} = I_{E1} \beta _2$$

我们可以写

$$I_{E2} = \beta _1 \beta _2 I_{B1}$$

因此，电流增益可以表示为

$$\beta = \frac{I_{E2}}{I_{B1}} = \frac{\beta _1 \beta _2 I_{B1}}{I_{B1}} = \beta _1 \beta_2$$

达林顿放大器的输入阻抗为

$Z_{in} = \beta_1 \beta_2 R_E .....$忽略r'e

在实践中，这两个晶体管放置在一个晶体管外壳中，三个端子从外壳中取出，如下面的图所示。

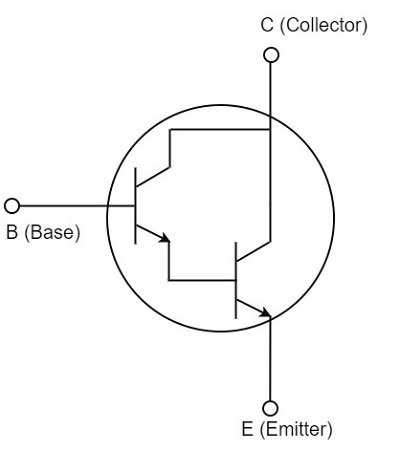
这个三端器件可以称为达林顿晶体管。达林顿晶体管就像一个具有高电流增益和高输入阻抗的单晶体管。

特性

以下是达林顿放大器的重要特性。

• 极高的输入阻抗（MΩ）。
• 极高的电流增益（数千）。
• 极低的输出阻抗（几欧姆）。

由于达林顿放大器的特性基本上与射极跟随器的特性相同，因此这两个电路用于类似的应用。

到目前为止，我们已经讨论了基于正反馈的放大器。晶体管电路中的负反馈有助于振荡器的运行。振荡器主题在振荡器教程中完全涵盖。