晶体管负载线分析

---

---

到目前为止，我们已经讨论了晶体管的不同工作区域。但在所有这些区域中，我们发现晶体管在放大区工作良好，因此它也被称为线性区。晶体管的输出是集电极电流和集电极电压。

输出特性

当考虑晶体管的输出特性时，对于不同的输入值，曲线如下所示。

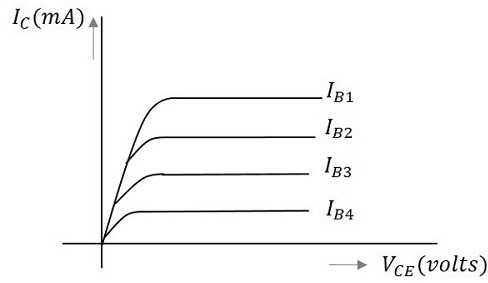
在上图中，输出特性是在不同基极电流I_B值下，集电极电流I_C和集电极电压V_CE之间绘制的。这里考虑了不同的输入值以获得不同的输出曲线。

负载线

当考虑最大可能集电极电流的值时，该点将出现在Y轴上，这也就是饱和点。同样，当考虑最大可能集电极发射极电压的值时，该点将出现在X轴上，即截止点。

当连接这两点画一条线时，这样的线可以称为负载线。之所以这样称呼，是因为它象征着负载处的输出。这条线在输出特性曲线上绘制时，会在一个称为工作点或静态点或简称为Q点的点处接触。

可以通过以下图形理解负载线的概念。

负载线是通过连接饱和点和截止点绘制的。这两点之间的区域是线性区域。晶体管在此线性区域中充当良好的放大器。

如果仅在给晶体管提供直流偏置但未施加输入信号时绘制此负载线，则此负载线称为直流负载线。而是在施加输入信号以及直流电压的条件下绘制的负载线，则称为交流负载线。

直流负载线

当给晶体管施加偏置并在其输入端未施加信号时，在此条件下绘制的负载线可以理解为直流条件。这里不会有放大，因为信号不存在。电路将如下图所示。

任何给定时间的集电极发射极电压值为

$$V_{CE} = V_{CC} - I_C R_C$$

由于V_CC和R_C是固定值，因此上述方程是一次方程，因此在输出特性上将是一条直线。这条线称为直流负载线。下图显示了直流负载线。

为了获得负载线，需要确定直线的两个端点。让这两个点分别为A和B。

获得A

当集电极发射极电压V_CE = 0时，集电极电流最大，等于V_CC/R_C。这给出了V_CE的最大值。显示如下

$$V_{CE} = V_{CC} - I_C R_C$$

$$0 = V_{CC} - I_C R_C$$

$$I_C = V_{CC}/R_C$$

这给出了集电极电流轴上的点A（OA = V_CC/R_C），如上图所示。

获得B

当集电极电流I_C = 0时，集电极发射极电压最大，将等于V_CC。这给出了I_C的最大值。显示如下

$$V_{CE} = V_{CC} - I_C R_C$$

$$= V_{CC}$$

(由于I_C = 0)

这给出了点B，这意味着（OB = V_CC）在集电极发射极电压轴上，如上图所示。

因此，我们得到了饱和点和截止点，并了解到负载线是一条直线。因此，可以绘制直流负载线。

交流负载线

前面讨论的直流负载线分析了当未施加交流电压时集电极电流和电压的变化。而交流负载线给出了峰峰值电压，或给定放大器的最大可能输出摆幅。

为了便于理解，我们将考虑共射放大器的交流等效电路。

从上图可以看出，

$$V_{CE} = (R_C // R_1) \times I_C$$

$$r_C = R_C // R_1$$

为了使晶体管能够作为放大器工作，它应该保持在放大区。静态点的选择方式使得最大输入信号偏移在负半周期和正半周期上是对称的。

因此，

$V_{max} = V_{CEQ}$ 和 $V_{min} = -V_{CEQ}$

其中V_CEQ是静态点的发射极-集电极电压

下图表示交流负载线，该负载线在饱和点和截止点之间绘制。

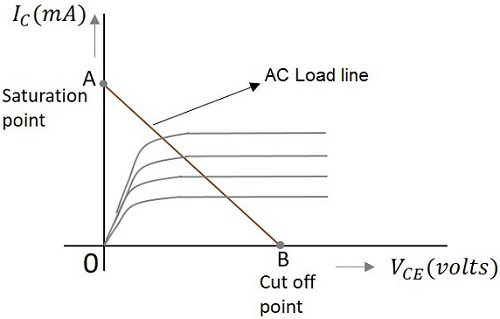
从上图可以看出，饱和点处的电流IC为

$$I_{C(sat)} = I_{CQ} + (V_{CEQ}/r_C)$$

截止点处的电压V_CE为

$$V_{CE(off)} = V_{CEQ} + I_{CQ}r_C$$

因此，对于相应的V_CEQ = V_CEQ / (R_C // R₁)，最大电流为

$$I_{CQ} = I_{CQ} * (R_C // R_1)$$

因此，通过添加静态电流，交流负载线的端点为

$$I_{C(sat)} = I_{CQ} + V_{CEQ}/ (R_C // R_1)$$

$$V_{CE(off)} = V_{CEQ} + I_{CQ} * (R_C // R_1)$$

交流和直流负载线

当交流和直流负载线在图形中表示时，可以理解它们并不相同。这两条线都与Q点或静态点相交。交流负载线的端点是饱和点和截止点。从下图可以看出。

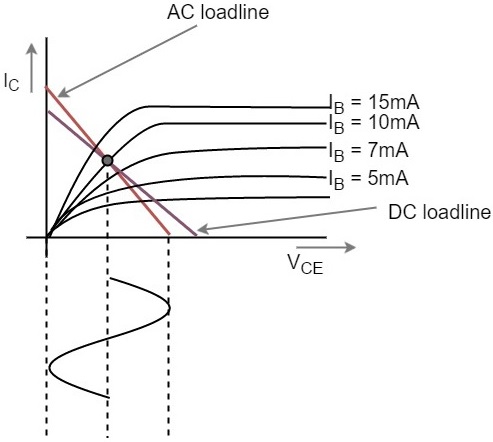
从上图可以看出，当基极电流IB值为10mA时，得到静态点（黑点）。这是交流和直流负载线相交的点。

在下一章中，我们将详细讨论静态点或工作点的概念。