晶体管偏置方法

---

---

晶体管电路中的偏置是通过使用两个直流电源V_BB和V_CC来完成的。经济上，最好将直流电源减少到一个电源而不是两个，这也会使电路更简单。

常用的晶体管偏置方法有

• 基极电阻法
• 集电极到基极偏置
• 带集电极反馈电阻的偏置
• 分压偏置

所有这些方法都具有相同的基本原理，即在零信号条件下从V_CC获得所需的I_B和I_C值。

基极电阻法

在这种方法中，一个高阻值的电阻R_B连接到基极，顾名思义。所需的零信号基极电流由V_CC提供，该电流流过R_B。基极发射极结正向偏置，因为基极相对于发射极是正的。

可以通过选择合适的基极电阻RB值，使所需的零信号基极电流以及由此产生的集电极电流（因为I_C = βI_B）流动。因此，需要知道R_B的值。下图显示了基极电阻偏置电路的样子。

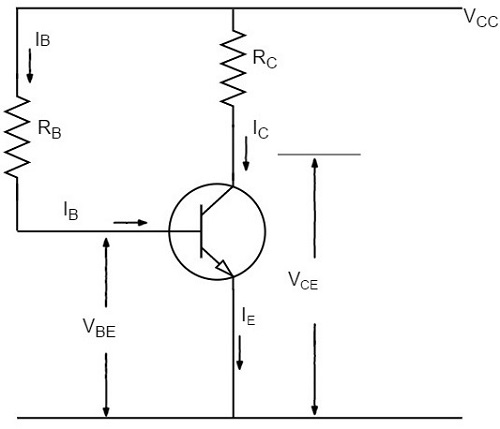
设I_C为所需的零信号集电极电流。因此，

$$I_B = \frac{I_C}{\beta}$$

考虑从V_CC、基极、发射极和地之间的闭合回路，同时应用基尔霍夫电压定律，我们得到，

$$V_{CC} = I_B R_B + V_{BE}$$

或者

$$I_B R_B = V_{CC} - V_{BE}$$

因此

$$R_B = \frac{V_{CC} - V_{BE}}{I_B}$$

由于V_BE通常比V_CC小得多，因此可以忽略前者而产生的误差很小。然后，

$$R_B = \frac{V_{CC}}{I_B}$$

我们知道V_CC是一个固定的已知量，而I_B则选择一个合适的值。由于R_B可以直接找到，因此这种方法称为固定偏置法。

稳定因子

$$S = \frac{\beta + 1}{1 - \beta \left ( \frac{d I_B}{d I_C} \right )}$$

在固定偏置偏置方法中，I_B与I_C无关，因此，

$$\frac{d I_B}{d I_C} = 0$$

将上述值代入前面的等式，

稳定因子，$S = \beta + 1$

因此，固定偏置中的稳定因子为（β+1），这意味着I_C的变化是I_CO任何变化的（β+1）倍。

优点

• 电路简单。
• 只需要一个电阻R_E。
• 偏置条件易于设置。
• 没有负载效应，因为基极-发射极结处没有电阻。

缺点

• 稳定性差，因为热量发展无法阻止。

• 稳定因子非常高。因此，存在热失控的可能性很大。

因此，这种方法很少使用。

集电极到基极偏置

集电极到基极偏置电路与基极偏置电路相同，只是基极电阻R_B连接到集电极，而不是连接到V_CC电源，如下面的图所示。

该电路有助于显着提高稳定性。如果I_C的值增加，则R_L上的电压增加，因此V_CE也增加。这反过来会降低基极电流I_B。此操作在某种程度上补偿了原始的增加。

需要给出零信号集电极电流I_C的R_B的所需值可以计算如下。

R_L上的压降将为

$$R_L = (I_C + I_B)R_L \cong I_C R_L$$

从图中，

$$I_C R_L + I_B R_B + V_{BE} = V_{CC}$$

或者

$$I_B R_B = V_{CC} - V_{BE} - I_C R_L$$

因此

$$R_B = \frac{V_{CC} - V_{BE} - I_C R_L}{I_B}$$

或者

$$R_B = \frac{(V_{CC} - V_{BE} - I_C R_L)\beta}{I_C}$$

应用KVL我们有

$$(I_B + I_C)R_L + I_B R_B + V_{BE} = V_{CC}$$

或者

$$I_B(R_L + R_B) + I_C R_L + V_{BE} = V_{CC}$$

因此

$$I_B = \frac{V_{CC} - V_{BE} - I_C R_L}{R_L + R_B}$$

由于V_BE几乎与集电极电流无关，我们得到

$$\frac{d I_B}{d I_C} = - \frac{R_L}{R_L + R_B}$$

我们知道

$$S = \frac{1 + \beta}{1 - \beta (d I_B / d I_C)}$$

因此

$$S = \frac{1 + \beta}{1 + \beta \left ( \frac{R_L}{R_L + R_B} \right )}$$

此值小于固定偏置电路获得的（1+β）。因此，稳定性有所提高。

该电路提供负反馈，从而降低了放大器的增益。因此，集电极到基极偏置电路的稳定性提高是以牺牲交流电压增益为代价的。

带集电极反馈电阻的偏置

在这种方法中，基极电阻R_B的一端连接到基极，另一端连接到集电极，顾名思义。在此电路中，零信号基极电流由V_CB决定，而不是由V_CC决定。

很明显，V_CB使基极-发射极结正向偏置，因此基极电流I_B流过R_B。这会导致零信号集电极电流在电路中流动。下图显示了带集电极反馈电阻的偏置电路。

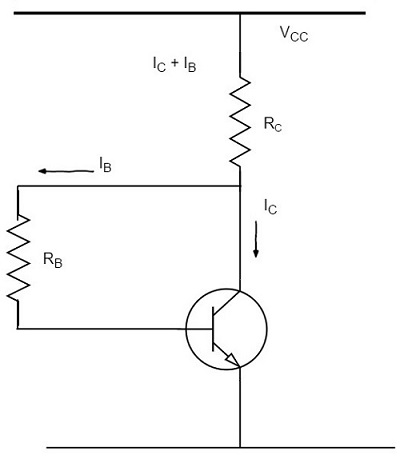
需要给出零信号电流I_C的R_B的所需值可以确定如下。

$$V_{CC} = I_C R_C + I_B R_B + V_{BE}$$

或者

$$R_B = \frac{V_{CC} - V_{BE} - I_C R_C}{I_B}$$

$$= \frac{V_{CC} - V_{BE} - \beta I_B R_C}{I_B}$$

由于$I_C = \beta I_B$

或者，

$$V_{CE} = V_{BE} + V_{CB}$$

或者

$$V_{CB} = V_{CE} - V_{BE}$$

由于

$$R_B = \frac{V_{CB}}{I_B} = \frac{V_{CE} - V_{BE}}{I_B}$$

其中

$$I_B = \frac{I_C}{\beta}$$

在数学上，

稳定因子，$S < (\beta + 1)$

因此，此方法比固定偏置提供了更好的热稳定性。

电路的Q点值显示为

$$I_C = \frac{V_{CC} - V_{BE}}{R_B/ \beta + R_C}$$

$$V_{CE} = V_{CC} - I_C R_C$$

优点

• 该电路简单，因为它只需要一个电阻。
• 对于较小的变化，此电路提供了一些稳定性。

缺点

• 该电路没有提供良好的稳定性。
• 该电路提供负反馈。

分压偏置法

在所有提供偏置和稳定性的方法中，分压偏置法是最突出的方法。在这里，使用了两个电阻R₁和R₂，它们连接到V_CC并提供偏置。发射极中使用的电阻R_E提供稳定性。

分压这个名称来自由R₁和R₂形成的分压器。R₂上的压降使基极-发射极结正向偏置。这导致在零信号条件下基极电流以及集电极电流流动。下图显示了分压偏置法电路。

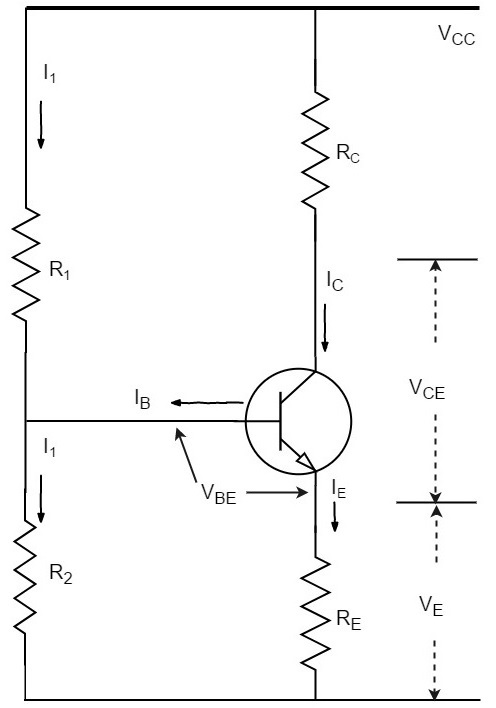
假设流过电阻R₁的电流为I₁。由于基极电流I_B非常小，因此可以合理地认为流过R₂的电流也是I₁。

现在让我们尝试推导出集电极电流和集电极电压的表达式。

集电极电流，I_C

从电路中可以看出，

$$I_1 = \frac{V_{CC}}{R_1 + R_2}$$

因此，电阻R₂上的电压为

$$V_2 = \left ( \frac{V_{CC}}{R_1 + R_2}\right ) R_2$$

将基尔霍夫电压定律应用于基极电路，

$$V_2 = V_{BE} + V_E$$

$$V_2 = V_{BE} + I_E R_E$$

$$I_E = \frac{V_2 - V_{BE}}{R_E}$$

由于I_E ≈ I_C，

$$I_C = \frac{V_2 - V_{BE}}{R_E}$$

从上述表达式可以看出，I_C不依赖于β。V_BE非常小，以至于I_C根本不受V_BE的影响。因此，该电路中的I_C几乎与晶体管参数无关，因此实现了良好的稳定性。

集电极-发射极电压，V_CE

将基尔霍夫电压定律应用于集电极侧，

$$V_{CC} = I_C R_C + V_{CE} + I_E R_E$$

由于I_E ≅ I_C

$$= I_C R_C + V_{CE} + I_C R_E$$

$$= I_C(R_C + R_E) + V_{CE}$$

因此，

$$V_{CE} = V_{CC} - I_C(R_C + R_E)$$

R_E在此电路中提供了极佳的稳定性。

$$V_2 = V_{BE} + I_C R_E$$

假设温度升高，则集电极电流I_C减小，这会导致R_E上的压降增加。由于R₂上的压降为V₂，它与I_C无关，因此V_BE的值减小。I_B的减小值倾向于将I_C恢复到原始值。

稳定因子

该电路的稳定因子方程获得如下

稳定因子 = $S = \frac{(\beta + 1) (R_0 + R_3)}{R_0 + R_E + \beta R_E}$

$$= (\beta + 1) \times \frac{1 + \frac{R_0}{R_E}}{\beta + 1 + \frac{R_0}{R_E}}$$

其中

$$R_0 = \frac{R_1 R_2}{R_1 + R_2}$$

如果R₀/R_E的比率非常小，则可以忽略R0/RE与1相比，稳定因子变为

稳定因子 = $S = (\beta + 1) \times \frac{1}{\beta + 1} = 1$

这是S的最小可能值，并导致最大可能的热稳定性。