分析下表中凸透镜成像时像距(v)随物距(u)变化的情况，并在不进行任何计算的情况下回答以下问题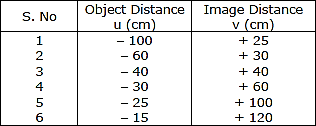：(a) 凸透镜的焦距是多少？请说明理由。(b) 哪个序号的观察结果不正确？你得出这个结论的依据是什么？(c) 选择合适的比例尺，为序号2的观察结果画出光路图。

(a) 从序号3可以看出，透镜的曲率半径（从透镜的光心到曲率中心的距离）是40厘米，因为物距(u)等于像距(v)，均为40厘米。

当物体放在凸透镜的曲率中心（或2F）时，它的像成在与透镜相同距离的另一侧。并且，我们知道焦距是曲率半径的一半。因此，透镜的焦距为+20厘米。

(b) 序号6不正确，因为物体放置在光心和焦点之间，则成的像是虚像、正立、放大的。因此，像距不应为正值。

(c) 已知

物距，$u=-60cm$

像距，$v=+30cm$

求：放大率，$m$。

解答

我们知道放大率的公式为：

$m=\frac {v}{u}$

代入所需的值，我们得到：

$m=\frac {30}{-60}$

$m=-\frac {1}{2}$

$m=-0.5$

因此，放大率的近似值为-0.5。

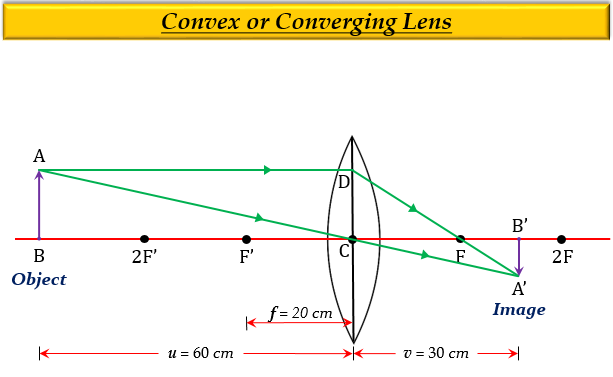
为了绘制序号2的光路图，我们需要找出焦距。

因此，根据透镜公式，我们知道：

$\frac {1}{f}=\frac {1}{v}-\frac {1}{u}$

代入所需的值，我们得到：

$\frac {1}{f}=\frac {1}{30}-\frac {1}{-60}$

$\frac {1}{f}=\frac {1}{30}+\frac {1}{60}$

$\frac {1}{f}=\frac {2+1}{60}$

$\frac {1}{f}=\frac {3}{60}$

$\frac {1}{f}=\frac {1}{20}$

$f=+20$

因此，焦距为20厘米。

Tutorialspoint

更新于：2022年10月10日

2K+浏览量

开启你的职业生涯

完成课程获得认证

开始学习