四边形面积

---

简介

四边形的面积是指四边形各边所包围的区域。四边形包含的领土数量决定了它的面积。让我们回顾一下四边形的定义。一个封闭的图形，由四条线段围成，称为四边形。四边形既有正规的，也有不规则的。等边四边形是指边长相等的四边形。不规则四边形是不规则的四边形。

四边形有六种不同的类型。正方形、矩形、平行四边形、梯形、菱形、风筝等。在本教程中，我们讨论了所有这些四边形的面积。我们将研究如何将四边形分成两个三角形，以及如何通过计算其四条边来计算其面积。我们还将学习计算每种不同四边形形状面积的公式。

四边形

在几何学中，四边形是一个封闭的图形，它是由连接四个点形成的，其中任意三个点不共线。一个四边形有4条边、4个角和4个顶点。四边形的所有四条边不一定相等。命名四边形时，必须考虑顶点的排列顺序。

例如，以下四边形应称为PQRS、QRSP、PSRQ或RSPQ。由于它们改变了生成四边形的顶点顺序，因此不能称为PRSQ或SQPR。一个标有PQRS的四边形有四条边：PQ、QR、RS和PS，以及两条对角线：PR和QS。

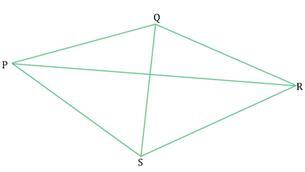
不同四边形的面积

四边形包含的领土数量决定了它的面积。四边形包括正方形、矩形、平行四边形、梯形、菱形、风筝等。

除了学习如何将四边形分成两个三角形外，您还将学习如何计算四边形的边数以确定其面积。此外，我们还将学习计算每种不同

正方形和矩形

正方形是一种四边形，其四条边长度相等，四个角的度数也相等，均为90度。如果正方形每条边的长度为a，则计算正方形面积的公式为边²

$$\mathrm{面积 =a^2, 其中\: a\: 是\: 边的\: 长度}$$

示例

边长为3厘米的正方形的面积为3²=9平方厘米

在矩形四边形中，一对对边相等且平行，每个角的度数为90度。如果矩形的长和宽分别为l和b，则计算矩形面积的公式为长×宽=lb

示例

长为2厘米、宽为1厘米的矩形的面积为lb=2(1)=2平方厘米

菱形和平行四边形

在菱形中，所有边长度相等，且成对的对边平行。对角相等，对角线相互垂直平分。如果d₁和d₂是两条对角线的长度，则菱形的面积由公式$\mathrm{\frac{1}{2}×d_1×d_2}$给出

示例

对角线长度分别为5厘米和8厘米的菱形的面积为$\mathrm{\frac{1}{2}×d_1×d_2=\frac{1}{2}×5×8=20}$平方厘米

在平行四边形中，成对的对边相等且平行。成对的对角相等，对角线互相平分。如果b是底边，h是平行四边形的高，则其面积由底×高=bh计算得出。

示例

底边为10厘米、高为4厘米的平行四边形的面积为bh=10(4)=40平方厘米

梯形

在梯形中，只有一对对边平行。如果a和b是两条平行对边的长度，h是它们之间的距离，即四边形的高，则梯形的面积由公式$\mathrm{\frac{1}{2}×(a+b)×h}$给出

示例

如果梯形中两条平行边的长度分别为5厘米和7厘米，它们之间的距离为4厘米，则其面积为$\mathrm{\frac{1}{2}×(a+b)×h=\frac{1}{2}×(5+7)×4=12×2=24 }$平方厘米

风筝

以下是几何图形风筝UVWZ，其中UV=UZ，VW=ZW

即邻边长度相等，对角线在点O处互相平分。

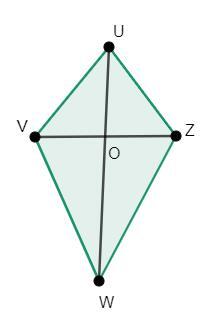
风筝的面积可以通过将两个三角形区域（即UVZ和VWZ）的面积相加来求得。也可以使用对角线的长度来求出风筝的面积。

如果d₁和d₂是两条对角线的长度，则风筝的面积由公式$\mathrm{\frac{1}{2}×d_1×d_2}$给出

一般四边形

以下四边形是一个一般四边形。它的面积可以通过将由于任何一条对角线而被分成两个三角形的面积相加来求得。

示例

$$\mathrm{ar(PQRS)=ar(PQS)+ar(QRS) 或 =ar(PQR)+ar(PSR)}$$

例题解析

1）计算对角线分别为16和14的风筝的面积。

答案：已知d₁=16和d₂=14

因此，给定风筝的面积确定为

$$\mathrm{\frac{1}{2}×d_1×d_2=\frac{1}{2}×16×14=112 \:平方单位}$$

2）使用四边形面积公式，求底边分别为12英寸和8英寸，高为4英寸的梯形的面积。

答案：已知a=12英寸，b=8英寸和h=4英寸

使用公式，

梯形的面积由下式给出

$$\mathrm{\frac{1}{2}×(a+b)×h=\frac{1}{2}×(12+8)×4=20×2=40\: 平方英寸}$$

3）使用海伦公式确定以下四边形的面积

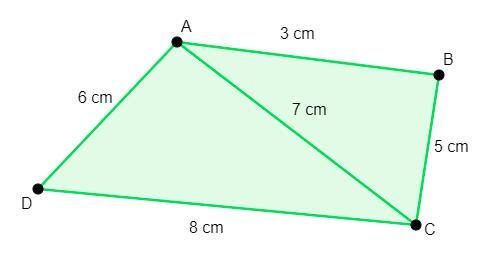
答案：使用海伦公式求三角形ABC的面积 -

$$\mathrm{s=\frac{3+5+7}{2}=7.5}$$

所以，

$$\mathrm{面积=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{7.5(7.5-3)(7.5-5)(7.5-7)}=\sqrt{42.1875}}$$

使用海伦公式求三角形ADC的面积 -

$$\mathrm{s=\frac{6+7+8}{2}=10.5}$$

所以，

$$\mathrm{面积=\sqrt{10.5(10.5-6)(10.5-7)(10.5-8)}=\sqrt{413.4375}}$$

因此，所需四边形的面积由下式给出

$$\mathrm{面积=\sqrt{42.1875}+\sqrt{413.4375}\: 平方单位}$$

结论

• 四边形的表面积是四边形边界之间区域的面积。

• 如上所述，有不同类型的四边形，以及各自的面积计算公式。

常见问题

1. 如何计算四边形的面积？

如果已知对角线和从顶点到对角线的垂线的长度，则四边形的面积计算如下 -

四边形的面积 = (1/2) 对角线长度 x 从其余两个顶点引出的垂线的长度之和。

2. 哪种四边形的边长相等？

一个封闭的图形，由四条线段围成，称为四边形。四边形既有正规的，也有不规则的。等边四边形是指边长相等的四边形。

3. 四边形的名称是什么？

四边形是一种有四条边和四个角的图形。任何边长相等的四边形都被称为正四边形。不规则四边形是指边长不相等的四边形，因为它不是正四边形。

4. 关于四边形，有三个事实是什么？

四边形是一种有四条边和四个角的多边形。四边形一词源于quad（意为四）和lateral（意为边）。四边形的内角之和为360度。

5. 四边形之间有什么联系？

四边形有很多不同的种类，但它们都有四条边、两条对角线，并且内角之和为360度。它们彼此之间都有联系，但它们都是独一无二的，并且具有不同的特性。