四边形：角和性质

---

介绍

在几何学中，四边形是一个四边多边形，具有四条边和四个角（顶点）。

这个名称来源于拉丁语单词 Quadra（四的变体）和 latus（意思是“边”）。

在参考其他多边形时，它也被称为四边形，源于希腊语“tetra”（意思是“四”）和“gon”（意思是“角”）。由于“gon”是“angle”（角）的字谜，因此它也被称为四边形或 4-角。

四边形有两种类型：简单（非自相交）和复杂（自相交或交叉）。

凸四边形或凹四边形是简单四边形。在本教程中，我们将讨论四边形及其类型以及性质。

四边形

四边形是几何学中一个封闭的物体，它通过连接四个点创建而成，其中任意三个点不共线。四边形有 4 条边、4 个角和 4 个顶点。四边形的所有四条边可能相等，也可能不相等。在命名四边形时，必须考虑顶点的排列顺序。例如，以下四边形应称为 PQRS、QRSP、PSRQ 或 RSPQ。由于它们改变了生成四边形的顶点顺序，因此不能称为 PRSQ 或 SQPR。带有字母 PQRS 的四边形有四条边：PQ、QR、RS 和 PS，以及两条对角线：PR 和 QS。

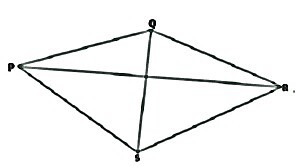
上述每个四边形都有其独特的特征。然而，所有四边形都有一些共同的特征。它们列在下面；

• 它们有四条边。

• 它们有四个角。

• 它们有四个顶点。

• 它们有两条对角线。

• 所有内角的总和为 360°。

我们将深入研究几种四边形的其他特性。可以使用以下四边形的特性来识别四边形。

正方形的性质

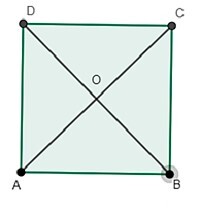
下面是几何图形正方形 ABCD，其中 AB=BC=CD=AD & AC=BD。

也就是说，所有边都相等，对角线也相等，每个角的度数为 90 度，即 $\mathrm{\angle A=\angle B=\angle C=\angle D=90^\circ}$

矩形的性质

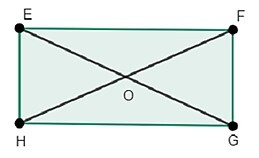
下面是几何图形矩形 EFGH，其中 EF=GH & FG=EH & EG=FH。

也就是说，对边相等，对角线相等，每个角的度数为 90 度 $\mathrm{\angle E=\angle F=\angle G=\angle H=90^\circ}$

平行四边形的性质

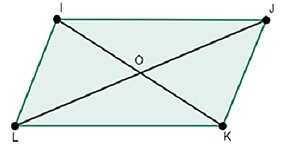
下面是几何图形平行四边形 IJKL，其中 IJ=LK & JK=IL

$$\mathrm{IJ\parallel LK,JK\parallel IL}$$

也就是说，对边相等且平行，对角线互相平分，它们在点 O 处相交。在平行四边形中，对角相等，即 $\mathrm{\angle I=\angle K\:\: \& \:\: \angle J=\angle L}$

梯形的性质

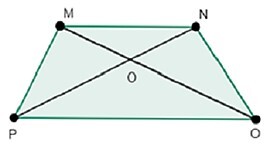
下面是几何图形梯形 MNOP，其中

$$\mathrm{MN\parallel PO}$$

也就是说，一对对边平行，这两条边称为底，另外两条边称为腰。当腰的长度相等时，该梯形称为等腰梯形。

菱形的性质

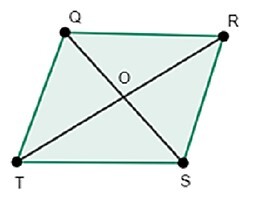
下面是几何图形菱形 QRST，其中 $\mathrm{QR=RS=ST=QT\:\: \&\:\: QR\parallel TS,QT\parallel RS}$

也就是说，所有边的长度都相等，并且成对的对边平行，对角线互相平分，在点 O 处相交。在菱形中，对角相等，即 $\mathrm{\angle Q=\angle S\:\: \&\:\: \angle R=\angle T}$

风筝的性质

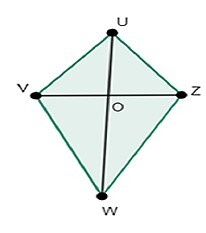
下面是几何图形风筝 UVWZ，其中 UV=UZ，VW=ZW

也就是说，邻边长度相等，对角线互相平分，在点 O 处相交。

四边形的角和性质

此性质指出，四边形所有角的和为 360°。

证明

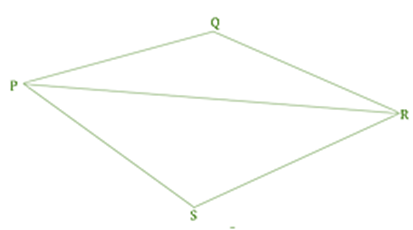
PQRS 是一个四边形，PQ、QR、RS 和 PR 是它的四条边，PR 是四边形 PQRS 的一条对角线。

由于对角线 PR，四边形 PQRS 被分成两个区域，即三角形 PSR 和 PQR。

我们知道三角形的角和性质，该性质指出三角形中三个角的和为 180 度。

在三角形 PSR 和三角形 PQR 中使用此三角形性质，我们得到以下等式

$$\mathrm{\angle PQR+\angle QPR+\angle QRP=180^\circ………………….. (1)}$$

$$\mathrm{\angle PSR+\angle SPR+\angle SRP=180^\circ……………………. (2)}$$

将等式 (1) 和 (2) 相加，我们得到：

$$\mathrm{\angle PQR+\angle QPR+\angle QRP+\angle PSR+\angle SPR+\angle SRP=180^\circ+180^\circ=360^\circ…… (3)}$$

注意：

$$\mathrm{\angle QPR+\angle SPR=\angle P}$$

$$\mathrm{\angle QRP+\angle SRP=\angle R}$$

$$\mathrm{\angle PQR=\angle Q\:\: \&\:\: \angle PSR=\angle S}$$

因此，等式 (3) 变为：

$$\mathrm{\angle P+\angle Q+\angle R+\angle S=360^\circ}$$

因此，我们证明了四边形中所有角的和为 360 度。

例题

1.求以下菱形四边形中未知角 x 的度数。

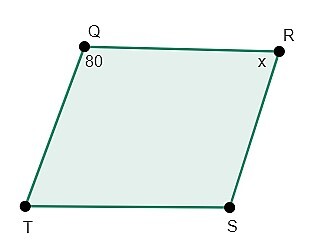
解 -

我们知道菱形中对角相等。因此，

$$\mathrm{\angle Q=\angle S=80^\circ \:\:\&\:\: \angle R=\angle T=x}$$

由于四边形中四个角的和为 360 度，因此 $\mathrm{\angle Q+\angle R+\angle S+\angle T=360^\circ}$

$$\mathrm{80+x+80+x=360^\circ}$$

$$\mathrm{2x+160=360}$$

$$\mathrm{2x=200}$$

$$\mathrm{x=100}$$

2.确定以下平行四边形 IJKL 中角 y 的度数。

解

我们知道平行四边形中对角相等。因此，$\mathrm{\angle I=\angle K=110^\circ \:\:\&\:\: \angle J=\angle L=x}$

由于四边形中四个角的和为 360 度，因此 $\mathrm{\angle I+\angle J+\angle K+\angle L=360^\circ}$

$$\mathrm{110+x+110+x=360^\circ L}$$

$$\mathrm{2x+220=360}$$

$$\mathrm{2x=140}$$

$$\mathrm{x=70}$$

3.确定以下矩形 EFGH 中 y 的值。

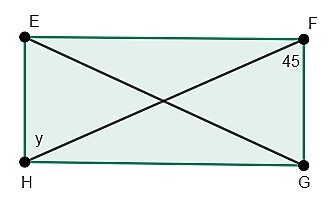
解

在矩形中，每个角的度数为 90 度，并且成对的对边相等且平行。

我们有 $\mathrm{ EF\parallel HG}$

因此，

$\mathrm{ \angle EHO= \angle OFG…………….}$（内错角相等）

因此，

$$\mathrm{y=45^o}$$

结论

封闭的四边形有四条边、四个顶点和四个角。它是一种多边形。为了创建它，连接四个不共线的点。四边形的内角总和始终为 360 度。

常见问题

1. 使四边形独特的因素是什么？

特殊四边形有许多独特的性质。梯形只有一组平行边。平行四边形有两组相等且平行的边。具有四个直角的平行四边形是矩形。

2. 四边形之间有什么联系？

四边形有很多不同的种类，但它们都有四条边、两条对角线以及内角之和为 360 度。它们彼此相关，但它们都是独特的，并且具有不同的特征。

3. 所有四边形都是平行四边形，对吗？

错误。由于每个平行四边形都是四边形，因此任何平行四边形都是四边形。

4. 四边形总是多边形吗？

四边形必须始终有四条边和四个角，并且边不能是曲线（因为它是一种多边形）。因此，多边形并不总是四边形，但四边形总是多边形。

5. 四边形的四条边大小都相等吗？

存在正四边形和不规则四边形。正四边形必须有四条相等的边、四个相等的角以及互相平分地交叉的对角线。唯一满足所有这些条件的四边形是正方形。