四边形$ABCD$是一个圆内接四边形，其对角线交于点$E$。如果$\angle DBC =70^\circ$，$\angle BAC=30^\circ$。求$\angle BCD$。此外，如果$AB=BC$，求$\angle ECD$。

已知

$ABCD$ 是一个圆内接四边形。

$\angle DBC =70⁰$，$\angle BAC=30⁰$ 且 $AB=BC$。

要求

我们需要求出 $\angle BCD$ 和 $\angle ECD$。

解答

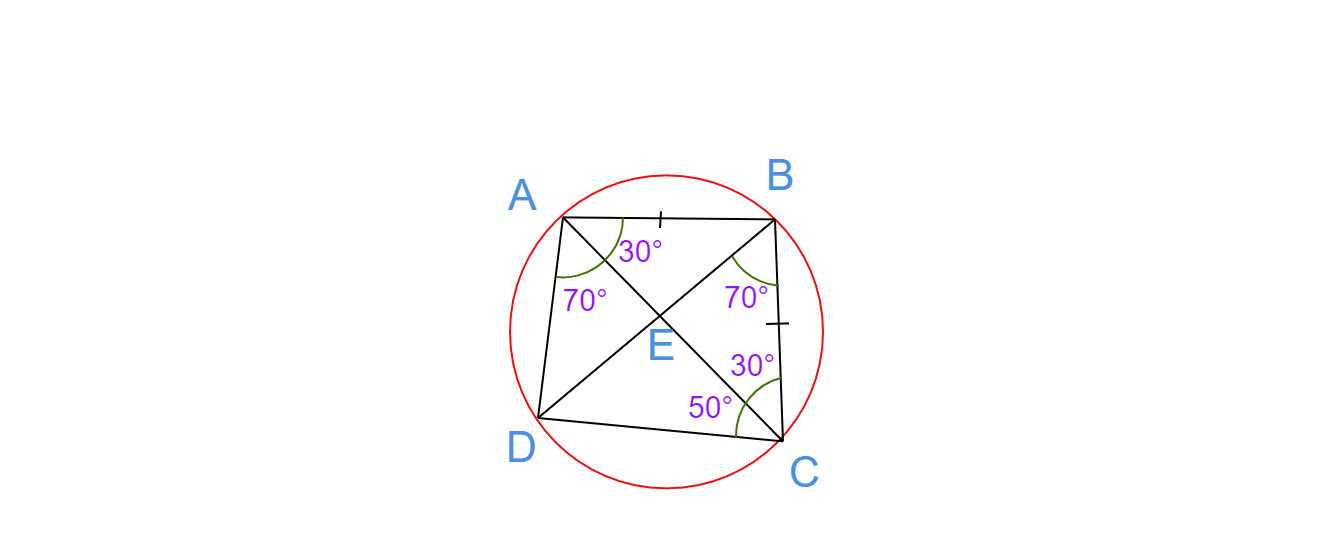
在圆内接四边形 $ABCD$ 中，已知 $AB=BC$。

因此，$\triangle ABC$ 是一个等腰三角形。

所以，$\angle BAC=\angle BCA=30°$。

$DC$ 是一条弦，它在圆上所对的圆周角分别是 $\angle DAC$ 和 $\angle DBC$。

因此，$\angle DAC=\angle DBC$ [同弧所对的圆周角相等]

$\angle DAC=\angle DBC= 70°$

$\angle BAD=\angle DAC+ \angle BAC$

$\angle BAD=70°+30°= 100°$

圆内接四边形的对角互补。

$\angle BAD+\angle BCD= 180°$

$100°+\angle BCD=180°$

$\angle BCD=180°-100°$

$\angle BCD=80°$

$\angle BCD=\angle BCA+\angle ACD$

我们已经知道，$\angle BCA=30°$。

$80°=30°+\angle ACD$

$\angle ACD=80°-30°$

$\angle ACD=\angle ECD=50°$

因此，$\angle BCD=80°$ 且 $\angle ECD=50°$。

教程点

更新于: 2022年10月10日

52 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习