数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律学
题目：我们需要画一条数轴并回答给定的问题。解答：(a) 因此，如果我们向 $-2$ 右侧移动 4 个数字，我们将到达 2。(b) 因此，如果我们向 1 左侧移动 5 个数字，我们将到达 $-4$(c) $-13$ 在数轴上位于 $-8$ 的左侧。因此，我们应该向左移动(d) $-1$ 在数轴上位于 $-6$ 的右侧。因此，我们应该向右移动。
题目：我们需要观察并找到给定的点。解答：(a) 点 $D$ 是 $+8$，点 $O$ 是 $0$。这意味着，相反方向为负。点 $F$ 位于 $O$ 下方 8 个单位。因此，点 $F$ 是 $-8$。(b) 点 $D$ 是 $+8$，点 $O$ 是 $0$。这意味着，相反方向为负。点 $G$ 位于 $O$ 下方 6 个单位。因此，点 $G$ 是一个负整数。(c) 点 $D$ 是 $+8$，点 $O$ 是 $0$。这意味着，相反方向为负。点 $B$ 位于 $O$ 上方 4 个单位。点 $E$ 位于 $O$ 下方 10 个单位。因此，点 $B$ 是 $+4$，点 $E$ 是 $-10$。(d) 点 $D$ ... 阅读更多
已知：给定的数字是 $-\frac{216}{125}$需要做：我们需要将给定的有理数表示为幂的形式。解答：我们知道，$(\frac{a}{b})^3 = \frac{a^3}{b^3}$$-\frac{216}{125}$$125 = 5\times 5\times 5 = (5)^3$$216 = 6\times 6\times 6 = 6^3$因此，$-\frac{216}{125} = -\frac{(6)^3}{(5)^3}$$= -(\frac{6}{5})^3$因此，$-\frac{-216}{125}$ 的幂形式是 $-(\frac{6}{5})^3$。
题目：我们需要找出哪个数字在数轴上位于另一个数字的右侧。解答：(a) 这里，$9>2$因此，9 在数轴上位于 2 的右侧。(b) 这里，$-3>-8$因此，$-3$ 在数轴上位于 $-8$ 的右侧。(c) 这里，$0>-1$因此，$0$ 在数轴上位于 $-1$ 的右侧。(d) 这里，$10>-11$因此，$10$ 在数轴上位于 $-11$ 的右侧。(e) 这里，$6>-6$因此，$6$ 在数轴上位于 $-6$ 的右侧。(f) 这里，$1>-100$因此，$1$ 在数轴上位于 $-100$ 的右侧。 阅读更多
题目：我们需要写出给定两数之间所有的整数。解答：(a) 这里，$-7
题目：我们需要写出四个负整数 (a) 大于 \( -20 \)。(b) 小于 $– 10$。解答：(a) 这里，$-20-10$因此，$-11、-12、-13、-14$ 是四个小于 $-10$ 的整数。
题目：我们需要判断给定的陈述是真还是假。解答：(a) 这里，$-8>-10$因此，\( -8 \) 在数轴上位于 \( -10 \) 的右侧。给定的陈述是正确的。 (b) 这里，$-50>-100$因此，\( -50 \) 在数轴上位于 \( -100 \) 的右侧。给定的陈述是错误的。 (c) 我们知道，$,....-3
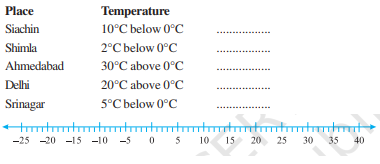
题目：我们需要将这些地方的温度用整数的形式表示。解答：(a) 低于 $0^o\ C$ 的 $10^o\ C$ 是 $-10^o\ C$低于 $0^o\ C$ 的 $2^o\ C$ 是 $-2^o\ C$高于 $0^o\ C$ 的 $30^o\ C$ 是 $+30^o\ C$高于 $0^o\ C$ 的 $20^o\ C$ 是 $+20^o\ C$低于 $0^o\ C$ 的 $5^o\ C$ 是 $-5^o\ C$因此，给定地点的温度用整数表示如下：锡亚琴 $-10^o\ C$西姆拉 $-2^o\ C$艾哈迈达巴德 $+30^o\ C$德里 $+20^o\ C$斯利那加 $-5^o\ C$(b) 给定地点的温度用整数表示如下：锡亚琴 $-10^o\ C$西姆拉 $-2^o\ C$艾哈迈达巴德 $+30^o\ C$德里 $+20^o\ C$斯利那加 $-5^o\ C$(c) 给定... 阅读更多
待解决问题：我们需要在每种情况下找到钟表指针停止时的数字。解答：(a) 1圈对应的时数 = 12小时$\frac{1}{2}$圈对应的时数 $= 12 \times \frac{1}{2}$$= 6$小时所以，指针会移动6个小时，停在6。(b) 1圈对应的时数 = 12小时$\frac{1}{2}$圈对应的时数 $= 12 \times \frac{1}{2}$$= 6$小时钟表指针的最终位置 $=2+6=8$所以，指针会移动6个小时，停在8。(c) 1圈对应的时数 = 12小时时数… 阅读更多
待解决问题：我们需要在每种情况下找到我们面向的方向。解答：我们知道，1圈 $= 360^o$因此，(a) $\frac{1}{2}$圈 $= \frac{360^o}{2} = 180^o$从东方向旋转$180^o$的方向是西。因此，如果我们开始面向东，并顺时针旋转$\frac{1}{2}$圈，那么我们将面向西。 (b) $1\frac{1}{2}$圈 $= \frac{3}{2}\times 360^o = 540^o$我们完成一整圈，然后从相同的起点再旋转半圈。这意味着，从东方向旋转$180^o$的方向是西。因此，如果我们开始面向东，并顺时针旋转$1\frac{1}{2}$圈… 阅读更多