数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：在三角形\( \mathrm{ABC} \)和\( \mathrm{DEF} \)中，\( \angle \mathrm{B}=\angle \mathrm{E} \)、\( \angle \mathrm{F}=\angle \mathrm{C} \)且\( \mathrm{AB}=3 \mathrm{DE} \)。 要求：我们必须选择正确的答案。解答：在三角形\( \mathrm{ABC} \)和\( \mathrm{DEF} \)中，\( \angle \mathrm{B}=\angle \mathrm{E} \)、\( \angle \mathrm{F}=\angle \mathrm{C} \)且\( \mathrm{AB}=3 \mathrm{DE} \)。 这意味着，$\angle \mathrm{A}=\angle \mathrm{D}$我们知道，如果两个三角形中对应两个角相同，则它们根据 AAA 相似性准则相似。这里，$\triangle ABC$ 和 $\triangle DEF$ 不满足任何全等规则（SAS、ASA、SSS）。因此，三角形\( \mathrm{ABC} \)和\( \mathrm{DEF} \)相似但不全等。 阅读更多
已知：在两个三角形\( \mathrm{DEF} \)和\( \mathrm{PQR} \)中，\( \angle \mathrm{D}=\angle \mathrm{Q} \)且\( \angle \mathrm{R}=\angle \mathrm{E} \)。要求：我们必须找到不正确的陈述。解答：在 $\triangle D E F$ 和 $\triangle PQR$ 中，$\angle D=\angle Q$$\angle R=\angle E$因此，根据 AAA 相似性，$\triangle D E F \sim \triangle Q R P$这意味着，$\angle F=\angle P$ (相似三角形的对应角)因此，$\frac{D F}{Q P}=\frac{E D}{R Q}=\frac{F E}{P R}$ 因此，(B) \( \frac{\mathrm{DE}}{\mathrm{PQ}}=\frac{\mathrm{EF}}{\mathrm{RP}} \) 不正确。 阅读更多
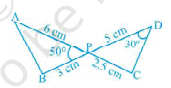
已知：两条线段\( \mathrm{AC} \)和\( \mathrm{BD} \)在点\( \mathrm{P} \)处相交，使得\( \mathrm{PA}=6 \mathrm{~cm} \)、\( \mathrm{~PB}=3 \mathrm{~cm} \)、\( \mathrm{PC}=2.5 \mathrm{~cm} \)、\( \mathrm{PD}=5 \mathrm{~cm} \)、\( \angle \mathrm{APB}=50^{\circ} \)和\( \angle \mathrm{CDP}=30^{\circ} \)。要求：我们必须找到\( \angle \mathrm{PBA} \)。解答：在 $\triangle A P B$ 和 $\triangle C P D$ 中，$\angle A P B=\angle C P D=50^{\circ}$ (对顶角)$\frac{\mathrm{AP}}{\mathrm{PD}}=\frac{6}{5}$..........(i)$\frac{\mathrm{BP}}{\mathrm{CP}}=\frac{3}{2.5}$$\frac{\mathrm{BP}}{\mathrm{CP}}=\frac{6}{5}$.......(ii)从 (i) 和 (ii) 中，我们得到，$\frac{AP}{PD}=\frac{BP}{CP}$因此，根据 SAS 相似性，$\triangle \mathrm{APB} \sim \triangle \mathrm{DPC}$这意味着，$\angle A=\angle D=30^{\circ}$ (相似三角形的对应角)角的和 ... 阅读更多
已知：在两个三角形\( \mathrm{ABC} \)和\( \mathrm{PQR} \)中，\( \frac{\mathrm{AB}}{\mathrm{QR}}=\frac{\mathrm{BC}}{\mathrm{PR}}=\frac{\mathrm{CA}}{\mathrm{PQ}} \)要求：我们必须选择正确的答案。解答：在 $\triangle A B C$ 和 $\triangle P Q R$ 中，$\frac{\mathrm{AB}}{\mathrm{QR}}=\frac{\mathrm{BC}}{\mathrm{PR}}=\frac{\mathrm{CA}}{\mathrm{PQ}}$我们知道，如果一个三角形的边与另一个三角形的边成比例，并且它们的对应角也相等，则这两个三角形根据 SSS 相似性相似。因此，$\triangle \mathrm{PQR} \sim \triangle \mathrm{CAB}$ 阅读更多
已知：菱形的两条对角线的长度分别为\( 16 \mathrm{~cm} \)和\( 12 \mathrm{~cm} \)。要求：我们必须找到菱形的边长。解答：我们知道，菱形的对角线是互相垂直平分。从图中，$AC=16\ cm$ 和 $BD=12\ cm$$\angle AOB=90^o$$AO=\frac{1}{2}AC$$=\frac{1}{2}(16)\ cm$$=8\ cm$$BO=\frac{1}{2}BD$$=\frac{1}{2}(12)\ cm$$=6\ cm$在直角三角形 AOB 中，使用勾股定理，$AB^2=AO^2+OB^2$$AB^2=8^2+6^2$$=64+36$$=100$$AB=\sqrt{100}$$=10\ cm$菱形的边长为 $10\ cm$。
**已知：**\( \Delta \mathrm{ABC} \sim \Delta \mathrm{EDF} \) 且 \( \Delta \mathrm{ABC} \) 不相似于 \( \Delta \mathrm{D} \mathrm{EF} \)**要求：**我们必须选择正确的答案。**解决方案：**我们知道，如果一个三角形的边与另一个三角形的边成比例，并且对应的角也相等，则这两个三角形根据SSS相似性相似。这意味着，$\triangle \mathrm{ABC} \sim \triangle \mathrm{EDF}$根据相似性性质，$\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{DF}}=\frac{\mathrm{AC}}{\mathrm{EF}}$这意味着，$\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{DF}}$$\mathrm{AB} . \mathrm{DF}=\mathrm{ED} . \mathrm{BC}$$\frac{\mathrm{BC}}{\mathrm{DF}}=\frac{AC}{EF}$ $\mathrm{BC} . \mathrm{EF}=\mathrm{AC} . \mathrm{DF}$$\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{AC}{EF}$ $\mathrm{AB} . \mathrm{EF}=\mathrm{ED} . \mathrm{AC}$因此，\( \mathrm{BC} \cdot \mathrm{DE}=\mathrm{AB} \cdot \mathrm{EF} \) 不正确。阅读更多
化石燃料（煤炭和石油）是地球上有限的资源，并且正在迅速枯竭。化石燃料的燃烧会导致大量的环境污染。因此，迫切需要利用非常规能源。
利用海浪能量的两种方法如下：1. 在海中设置浮动发电机，这些发电机将随着海浪上下移动。这种运动将驱动发电机发电。2. 让海浪在大型管道内上下移动，这样当海浪上升时，管道内的空气会被压缩，这种压缩空气可以用来转动发电机的涡轮机发电。
使用化石燃料的一些环境后果，因为它们是由死亡动植物的残骸形成的。1. 燃烧会导致空气污染，增加空气中的二氧化碳。2. 全球变暖3. 酸雨4. 溢油可以通过以下措施来控制燃烧化石燃料造成的污染：（a）通过在车辆中使用催化转化器，可以减少车辆中石油燃料燃烧产生的空气污染，因为它可以将有害气体转化为无害气体。（b）通过用水冲洗和清洗烟雾中的酸性气体，可以减少燃煤热力发电厂造成的空气污染... 阅读更多
给定陈述：“各种来源的能量被认为来源于太阳。”是的，同意给定的陈述，因为太阳被认为是地球上的主要能源，因为所有形式的能量都是直接或间接地来源于太阳。通过下面给出的各种形式的能量，我们可以理解太阳是如何成为主要能源的：1. 风能：风是由于地球受热不均而产生的压差造成的。2. 海洋热能：海洋表面温度与深层水温之间的差异... 阅读更多