已知:BD 和 CE 相交于点 P。 求证:△PBC ∽ △PDE。解答:从图中,∠BPC = ∠EPD (对顶角) PB/PD = 5/10 = 1/2 ……(i) PC/PE = 6/12 = 1/2 ……(ii) 从 (i) 和 (ii) 可以得到,PB/PD = PC/PE。这里,△PBC 的一个角等于△PDE 的一个角,并且包含这些角的两条边成比例。因此,这两个三角形相似。因此,根据 SAS 相似性定理,△PBC ∽ △... 阅读更多
已知:D 是△PQR 边 QR 上的一点,使得 PD⊥QR。求证:△PQD ∽ △RPD。解答:在△PQD 和△RPD 中,PD = PD (公共边) ∠PDQ = ∠PDR = 90° 这里,没有其他边或角相等,所以我们可以说△PQD 与△RPD 不相似。
已知:一个三角形,边长分别为 25cm、5cm 和 24cm。求证:该三角形是否为直角三角形。解答:设 a = 25cm,b = 5cm,c = 24cm,则 b² + c² = 5² + 24² = 25 + 576 = 601 a² = 25² = 625 这里,b² + c² ≠ a² 给定的边长不满足勾股定理。因此,给定的三角形不是直角三角形。
已知:△DEF ∽ △RPQ。求证:∠D = ∠R 和 ∠F = ∠P。解答:我们知道,如果两个三角形相似,则它们的对应角相等。这里,△DEF ∽ △RPQ。因此,∠D = ∠R ∠E = ∠P ∠F = ∠Q
已知:A 和 B 分别是三角形 PQR 的边 PQ 和 PR 上的点,使得 PQ = 12.5cm,PA = 5cm,BR = 6cm,PB = 4cm。求证:AB∥QR。解答:QA = QP - PA = 12.5 - 5 = 7.5cm PA/AQ = 5/7.5 = 50/75 = 2/3 ……(i) PB/BR = 4/6 = 2/3 ……(ii) 从 (i) 和 (ii) 可以得到,PA/AQ = PB/BR。根据比例线段定理的逆定理,AB∥QR 阅读更多
已知:S 是△PQR 的边 PQ 上的一点,使得 PS = QS = RS。求解:选择正确答案。解答:设∠PRS = ∠1,∠RPS = ∠2,∠SRQ = ∠3,∠RQS = ∠4 PS = QS = RS 在△PSR 中,PS = RS,则∠1 = ∠2 同理,在△RSQ 中,∠3 = ∠4 (对应角) 在△PQR 中,∠P + ∠Q + ∠R = 180° ∠2 + ∠4 + ∠1 + ∠3 = 180° ∠1 + ∠3 + ∠1 + ∠3 = 180° 2(∠1 + ∠3) = 180° ∠1 + ∠3 = 180°/2 = 90° ∠R = 90° 因此,在△... 阅读更多
已知:在三角形 ABC 和 DEF 中,AB/DE = BC/FD。求解:选择正确的答案。解答:已知,AB/DE = BC/FD 根据比例线段定理的逆定理,如果 ABC ∽ DEF,则,∠B = ∠D ∠A = ∠E ∠C = ∠F
已知:△ABC ∽ △QRP,ar(ABC)/ar(PQR) = 9/4,AB = 18cm,BC = 15cm。求解:求 PR 的长度。解答:我们知道,两个相似三角形的面积之比等于它们对应边长的平方之比。因此,ar(△ABC)/ar(△QRP) = (BC)²/(RP)² ar(△ABC)/ar(△PQR) = 9/4 (已知) 则,15²/RP² = 9/4 RP² = (225 × 4)/9 RP² = 100 PR = 10cm 阅读更多
已知:△ABC ∽ △PQR,BC/QR = 1/3 求解:求 ar(PRQ)/ar(BCA)。解答:△ABC ∽ △PQR BC/QR = 1/3 我们知道,两个相似三角形的面积之比等于它们对应边长的平方之比。因此,ar(△PRQ)/ar(△BCA) = (QR)²/(BC)² = (QR/BC)² = (3/1)² = 9/1 = 9
已知:\( \triangle \mathrm{ABC} \sim \triangle \mathrm{DFE} \),\( \angle \mathrm{A}=30^{\circ} \),\( \angle \mathrm{C}=50^{\circ} \),\( \mathrm{AB}=5 \mathrm{~cm} \),\( \mathrm{AC}=8 \mathrm{~cm} \) 和 \( \mathrm{DF}=7.5 \mathrm{~cm} \)。求解:我们必须选择正确的答案。解:根据图形,\(\angle B=\angle F =180^{\circ}-(30^{\circ}+50^{\circ}) =100^{\circ}\) \(AB=5 \mathrm{~cm}\),\(AC=8 \mathrm{~cm}\) 和 \(DF=7.5 \mathrm{~cm}\) 因此,\(\frac{AB}{DF}=\frac{AC}{DE}\) \(\frac{5}{7.5}=\frac{8}{DE}\) \(DE=\frac{8 \times 7.5}{5} =12 \mathrm{~cm}\) 因此,\(DE=12 \mathrm{~cm}\),\(\angle F=100^{\circ}\)

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP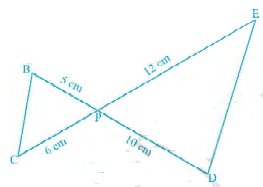 "
"
