数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
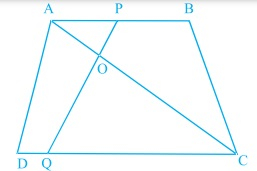
已知：梯形 ABCD 中，AB∥DC，P 和 Q 分别是 AD 和 BC 上的点，使得 PQ∥DC。PD=18cm，BQ=35cm，QC=15cm。求解：我们需要求解 AD。解：连接 BD。在三角形 ABD 中，PO∥AB [因为 AB∥CD∥PQ] 因此，根据比例线段定理，⇒ DP/AP = DO/OB ……(i) 在三角形 BDC 中，OQ∥DC [因为 AB∥CD∥PQ] 因此，根据比例线段定理，BQ/QC = OB/OD ⇒ … 阅读更多
已知：两个相似三角形的对应边之比为 2:3。较小三角形的面积为 48 cm²。求解：求较大三角形的面积。解：已知，两个相似三角形的对应边之比 = 2:3 = 2/3 较小三角形的面积 = 48 cm² 根据两个相似三角形面积的性质，面积比 = (对应边比)² ⇒ 面积(较小三角形) / 面积(较大三角形) = (2/3)² ⇒ 48 / 面积(较大三角形) = 4/9 ⇒ 较大三角形的面积 = (48×9)/4 = 12×9 = 108 cm²
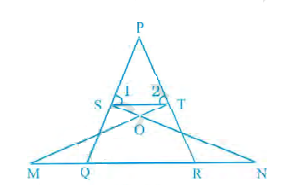
已知：在三角形 PQR 中，N 是 PR 上的一点，使得 QN⊥PR。PN·NR=QN²。求证：∠PQR=90°。证明：PN·NR=QN² PN·NR=QN·QN 这意味着，PN/QN=QN/NR ……(i) 在三角形 QNP 和三角形 RNQ 中，PN/QN=QN/NR ∠PNQ=∠RNQ 因此，根据 SAS 相似性，∠QNP～∠RNQ 这意味着，∠PQN=∠QR … 阅读更多
已知：边长为 8cm 的等边三角形。求解：求等边三角形的高。解：三角形 ABC 是等边三角形。 [已知] AD⊥BC [已知] 在三角形 ADB 和三角形 ADC 中，AB=BC [等边三角形的边长相等] ∠1=∠2=90° AD=AD [公共边] 因此，根据 RHS 全等性，三角形 ADB ≅ 三角形 ADC ⇒ BD=DC [全等三角形的对应边相等] 这意味着，BD=DC=BC/2 = 8/2 = 4 cm 因此，根据勾股定理，在直角三角形 ADB 中，AD²+BD²=AB² ⇒ AD²+(4)²=(8)² ⇒ … 阅读更多
已知：△ABC～△DEF，AB=4cm，DE=6cm，EF=9cm，FD=12cm。求解：求△ABC的周长。解：△ABC～△DEF 这意味着，AB/ED = BC/EF = AC/DF 4/6 = BC/9 = AC/12 4/6 = BC/9 BC = (4×9)/6 BC = 6 cm AC = (6×12)/9 AC = 8 cm 因此，△ABC的周长 = AB + BC + AC = 4 + 6 + 8 = 18 cm △ABC的周长是 18cm。阅读更多
"
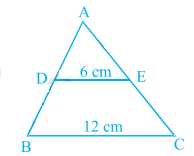
已知：DE∥BC。求解：求 ar(ADE) 和 ar(DECB) 的比值。解：在三角形 ABC 和三角形 ADE 中，∠ABC=∠ADE (同位角) ∠ACB=∠AED (同位角) ∠A=∠A 因此，根据 AA 相似性，三角形 ABC ～ 三角形 ADE 这意味着，ar(三角形 ADE) / ar(三角形 ABC) = (DE/BC)² = 6²/12² = (1/2)² = 1/4 令 ar(三角形 ADE) = k 这意味着，ar(三角形 ABC) = 4k ar(DECB) = ar(ABC) - ar(ADE) = 4k - k = 3k 因此，ar(… 阅读更多
已知：梯形 PQRS 的对角线在点 O 相交，PQ∥RS 且 PQ=3RS。求解：求三角形 POQ 和三角形 ROS 的面积之比。解：在三角形 POQ 和三角形 ROS 中，∠POQ=∠ROS (对顶角) ∠OPQ=∠ORS (内错角，因为 PQ∥RS) 因此，三角形 POQ～三角形 ROS (根据 AA 相似) 我们知道，如果两个三角形相似，则两个三角形的面积之比等于对应边之比的平方。因此，ar(三角形 POQ) / ar(三角形 ROS) = PQ²/RS² = (3RS)²/RS² = 9RS²/RS² = 9/1 三角形 POQ 和 … 阅读更多
"
已知：AB∥DC，AC和PQ相交于点O。
"
已知：∠1=∠2，并且△NSQ ≅ △MTR
"
求解：求使DE∥AB的x值。