已知:线段\( \mathrm{DF} \)与三角形\( \mathrm{ABC} \)的边\( \mathrm{AC} \)相交于点\( \mathrm{E} \),使得\( \mathrm{E} \)是\( \mathrm{CA} \)的中点,且\( \angle \mathrm{AEF}=\angle \mathrm{AFE} \)。要求:我们必须证明\( \frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BF}}{\mathrm{CE}} \)证明:在 $AB$ 上取一点 $G$,使得 $CG \| EF$。$E$ 是 $CA$ 的中点这意味着,$CE=AE$..........(i)在 $\triangle ACG$ 中,$CG \| EF$ $E$ 是 $CA$ 的中点。这意味着,$CE=GF$........(ii)在 $\triangle BCG$ 和 $\triangle BDF$ 中, ... 阅读更多
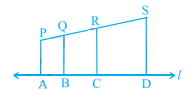
已知:\( \mathrm{PA}, \mathrm{QB}, \mathrm{RC} \)和\( \mathrm{SD} \)都垂直于直线\( l \),\( \mathrm{AB}=6 \mathrm{~cm} \),\( \mathrm{BC}=9 \mathrm{~cm}, CD=12 \mathrm{~cm} \)和\( S P=36 \mathrm{~cm} \)。要求:我们必须求\( P Q, Q R \)和\( R S \)。证明:直线 $P A, Q B, R C$ 和 $S D$ 相互平行。这意味着,直线 $\mathrm{PA}, \mathrm{QB}, \mathrm{RC}$ 和 $\mathrm{SD}$ 垂直于直线 $\mathrm{l}$。根据截距定理,当两条平行线被两条相交线截取时,所创建的线段之间的比率。这意味着,$\frac{\mathrm{PQ}}{\mathrm{AB}}=\frac{\mathrm{QR}}{ \mathrm{BC}}=\frac{\mathrm{RS}}{\mathrm{CD}}=\frac{\mathrm{PS}}{ ... 阅读更多
已知:\( \mathrm{O} \)是梯形\( \mathrm{ABCD} \)的对角线\( \mathrm{AC} \)和\( \mathrm{BD} \)的交点,其中\( \mathrm{AB} \| \mathrm{DC} \)。过\( \mathrm{O} \),作一条线段\( \mathrm{PQ} \)平行于\( \mathrm{AB} \),分别交\( \mathrm{AD} \)于\( \mathrm{P} \)和\( \mathrm{BC} \)于\( \mathrm{Q} \)。要求:我们必须证明\( \mathrm{PO}=\mathrm{QO} \)。证明:在 $\triangle ABD$ 和 $\triangle POD$ 中,$PO \| AB$ $\angle D =\angle D$ (公共角)$\angle ABD =\angle POD$ ... 阅读更多
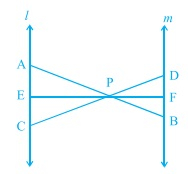
已知:\( l \| \mathrm{m} \)且线段\( \mathrm{AB}, \mathrm{CD} \)和\( \mathrm{EF} \)在点\( \mathrm{P} \)处共点。要求:我们必须证明\( \frac{\mathrm{AE}}{\mathrm{BF}}=\frac{\mathrm{AC}}{\mathrm{BD}}=\frac{\mathrm{CE}}{\mathrm{FD}} \)。证明:在 $\triangle APC$ 和 $\triangle BPD$ 中$\angle APC=\angle BPD$ (对顶角)$\angle PAC=\angle PBD$ (内错角)因此,根据 AA 相似性,$\triangle APC \sim \triangle BPD$这意味着,$\frac{AP}{PB}=\frac{AC}{BD}=\frac{PC}{PD}$..........(i)在 $\triangle APE$ 和 $\triangle BPF$ 中$\angle A ... 阅读更多
已知:在四边形\( \mathrm{ABCD} \)中,\( \angle \mathrm{A}+\angle \mathrm{D}=90^{\circ} \)。要求:我们必须证明\( \mathrm{AC}^{2}+\mathrm{BD}^{2}=\mathrm{AD}^{2}+\mathrm{BC}^{2} \)。证明:延长 $AB$ 和 $CD$ 交于 $E$。连接 $AC$ 和 $BD$。在三角形 $AED$ 中,$\angle A+\angle D =90^{\circ}$因此,$\angle A+\angle D+\angle E =180^{\circ}$$\angle E=180^{\circ}-(\angle A+\angle D)$$=90^{\circ}$$A D^{2}=A E^{2}+D E^{2}$......(i)在 $\triangle BEC$ 中,根据勾股定理,$B C^{2}=B E^{2}+E F^{2}$.........(ii)将 (i) 和 (ii) 相加,得到,$A D^{2}+B C^{2}=A E^{2}+D E^{2}+B E^{2}+C E^{2}$..........(iii)在 $\triangle AEC$ 中,根据勾股定理,$A C^{2}=A E^{2}+C E^{2}$.....(iv)在 $\triangle BED$ 中,根据勾股定理,$B D^{2}=B E^{2}+D E^{2}$.......(v)将 (iv) 和 (v) 相加,得到,$A C^{2}+B D^{2}=A E^{2}+C E^{2}+B E^{2}+D ... 阅读更多
**已知:**PQR是一个直角三角形,∠Q=90°,且QS⊥PR。PQ=6cm,PS=4cm。
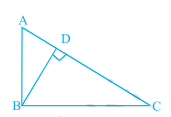
**已知:**ABC是一个直角三角形,∠B=90°,且BD⊥AC。AD=4cm,CD=5cm。
**已知:**一根5米长的梯子靠在一面竖直的墙上,梯子的顶端到达墙上4米高的地方。梯子的底部向墙移动1.6米。
**已知:**从城市A到城市B,有一条途径城市C的路线,使得AC⊥CB,AC=2x公里,CB=2(x+7)公里。现在计划修建一条26公里长的高速公路,直接连接城市A和城市B。

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP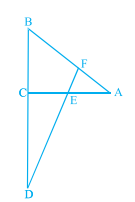 "
"

 "
"
 "
"
 "
"
 "
"