数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
正确答案：(c) Pb 解释：图中讨论的元素是碳。碳 (C) 和铅 (Pb) 都属于 IVA 族。
解题思路：我们需要判断给定的陈述是真是假。解答：(i) 我们知道，如果一个数能被另一个数整除，那么它就能被另一个数的因数整除。因此，如果一个数能被 9 整除，它就能被 3 整除，但反之不一定成立。例如，12 和 15 能被 3 整除，但不能被 9 整除。因此，如果一个数能被 3 整除，它可能不能被 9 整除。给定的陈述是错误的。(ii) 我们知道，如果一个数能被另一个数整除，那么它就能被另一个数的因数整除。因此，… 阅读更多
已知：$3\ 7$ $+ A\ B$ ----------- $9\ A$ 解题思路：我们需要解这个算术题。解答：$7+B=A$ $3+A=9$ 如果 $A=6$，则 $B=6-7=-1$，这是不可能的。这意味着，十位数进位为 1。这意味着，$3+A+1=9$ $A=9-4=5$ 十位数进位为 1。$\Rightarrow 7+B=10+A=10+5=15$ 因此，$7+B=15$ $B=15-7=8$
解题思路：我们需要证明算术题 $4 \times \overline{AB}=\overline{CAB}$ 没有解。解答：$4 \times \overline{\mathrm{AB}}=\overline{\mathrm{CAB}}$ $\overline{\mathrm{AB}}$ 是一个两位数，$\overline{\mathrm{CAB}}$ 是一个三位数。$4 \times \overline{\mathrm{AB}}=\overline{\mathrm{CAB}}$ 这意味着，$ A\ B$ $\times 4$--------------$C\ AB$ 这意味着，$4 \times B$ 是一个个位数为 $B$ 的数。没有这样一个数字，当乘以 4 时，个位数仍然相同。因此，这个算术题没有解。
解题思路：我们需要确定给定表达式的项及其系数。解答：(i) $7x^2yz - 5xy$ 项 系数 $7x^2yz$ $7$ $-5xy$ $-5$ (ii) $x^2 + x + 1$ 项 系数 $x^2$ $1$ $x$ $1$ $1$ $1$ (iii) $3x^2y^2 - 5x^2y^2z^2 + z^2 + 1$ 项 系数 $3x^2y^2$ $3$ $-5x^2y^2z^2$ $-5$ $z^2$ $1$ $1$ $1$ (iv) $9- ab + be-ca$ 项 系数 $9$ $9$ $-ab$ $-1$ $be$ $1$ $-ca$ $-1$ (v) $\frac{a}{2}+\frac{b}{2}-ab$ 项 系数 $\frac{a}{2}$ $\frac{1}{2}$ $\frac{b}{2}$ $\frac{1}{2}$ $-ab$ $-1$ (vi) $2x - 0.3xy + 0.5y$ 项 系数 $2x$ $2$ $-0.3xy$ $-0.3$ $0.5y$ $0.5$
解题思路：我们需要将给定的多项式分类为单项式、二项式、三项式。解答：单项式：只有一个项的多项式称为单项式。二项式：二项式是一个由两项之和组成的多项式。三项式：三项式是一个由三项组成的多项式。(i) 在给定的多项式中，有两项 (x, y)。因此，给定的多项式是一个二项式。(ii) 在给定的多项式中，有一项 (1000)。因此，给定的多项式是一个单项式。(iii) 在给定的多项式中，有四项 (x, x^2, x^3, x^4)。因此，给定的多项式不属于任何类别。(iv) 在给定的多项式中，有三项 (7, a, … 阅读更多
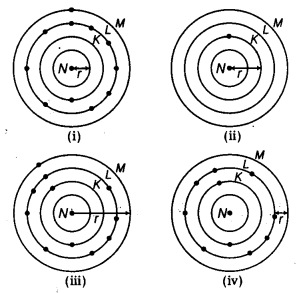
\正确答案：(b) (ii) 和 (iii) 解释：原子半径是原子核与最外层电子壳层之间的距离。因此，(ii) 和 (iii) 是正确的表示方法。
虹膜是人眼的一部分，它通过调节瞳孔的大小来控制进入眼睛的光量，并赋予眼睛其独特的颜色。
已知：$94 - 49$ 解题思路：我们需要求 $94 - 49$ 除以 (i) 9。(ii) 5 的商。解答：(i) 我们知道，当 $ab-ba$ 除以 9 时，商为 $(a-b)$。给定数字 94 和 49 的数字是反向的。这里，$a = 9, b = 4$ $a-b=9-4=5$ 如果 $94 -49$ 除以 9，则商为 $a-b=5$。(ii) 我们知道，当 $ab-ba$ 除以 $(a-b)$ 时，商为 5。给定数字 94 和 49 的数字是反向的。这里，$a = 9, b = 4$ $a-b=9-4=5$ 如果 $94 -49$ 除以 5，则商为 9。
已知：将数字 985 与另外两个通过循环排列 985 的数字得到的数字相加，其和分别被 111、22 和 37 除。 求：求出每种情况下商的值。 解：已知数字为 985 通过循环排列其数字得到的另外两个数字是 859 和 598 这些数字的形式为 $\overline{abc}、\overline{bca}、\overline{cba}$ 因此，如果 985 + 859 + 598 被 111 除，则商为 a + b + c = 9 + 8 + 5 = 22 如果该和被 22 除，则商为 111。 如果该和被 37 除，则商为 3(a+b+c)=3(22)=66。