数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
位于活性顺序靠前的金属通常以氧化物形式存在，这些氧化物相当稳定，因此通过电解还原法提取。而位于中间位置的金属，则首先将其转化为氧化物，然后用碳还原。不能采用相同的方法，因为活性顺序靠前的金属比碳更易与氧结合。从氯化钠中提取钠金属的过程：采用熔融氯化钠进行电解还原以生产钠金属。金属沉积在阴极，氯气在阳极释放。阴极：$Na^+ + e^- → Na$阳极… 阅读更多
(a)酯化反应：羧酸和醇在浓硫酸存在下反应生成具有甜味的酯的过程。$\overset{CH_{3}COOH}{乙酸}+\overset{CH_{3}CH_{2}OH}{乙醇}\xrightarrow[(浓H_{2}SO_{4})]{酸}CH_{3}COOC_{2}H_{5}+H_{2}O$皂化反应：酯和氢氧化钠反应生成酸的钠盐和醇的过程。$CH_{3}COOC_{2}H_{5}+NaOH\rightarrow CH_{3}COONa+C_{2}H_{5}OH$(b) 下面展示了在学校实验室中展示酯形成的活动：在试管中取1毫升冰醋酸和1毫升乙醇以及几滴浓硫酸。将试管在水浴中加热5分钟，保持试管在装有… 阅读更多
肥皂和洗涤剂的化学成分区别如下：肥皂是一些长链羧酸的钠（Na）盐或钾（K）盐，而洗涤剂是铵盐或硫化盐，或长链羧酸（COOH）。肥皂不能与硬水起泡，但洗涤剂可以与硬水和软水起泡。肥皂是可生物降解的，可以分解成更简单的物质，但洗涤剂是不可生物降解的，可以分解成更简单的物质。肥皂是温和的清洁剂，而洗涤剂是强效清洁剂，在去除油污方面更有效。… 阅读更多
(a) 元素的化合价由其外层电子壳层中的电子数决定。因此，从元素的电子构型获得的价电子数决定了化合价，即元素为达到惰性气体构型而失去、获得或共享的电子数。原子序数为9（电子构型：2, 7）的元素的化合价为1，因为其最外层电子壳层中的价电子数为7，所以它只需要一个电子就能达到惰性气体构型。(b) (i) 元素D (19) 在其最外层电子壳层中只有一个电子。其电子构型为2，… 阅读更多
已知：圆的弦在圆心处张成一个$\theta$角。弦截取的劣弧面积是圆面积的八分之一。要求：我们必须证明$8 \sin \frac{\theta}{2} \cos \frac{\theta}{2}+\pi=\frac{\pi \theta}{45}$。解：设弦AB在半径为r的圆的圆心处张成一个$\theta$角。圆的面积=$\pi r^2$劣弧ACB的面积=$(\frac{\pi \theta}{360^{\circ}}-\sin \frac{\theta}{2} \cos \frac{\theta}{2})$根据题意，劣弧ACB的面积=圆面积的$\frac{1}{8}$因此，$\pi r^{2}=8$（劣弧ACB的面积）$\Rightarrow \pi$… 阅读更多
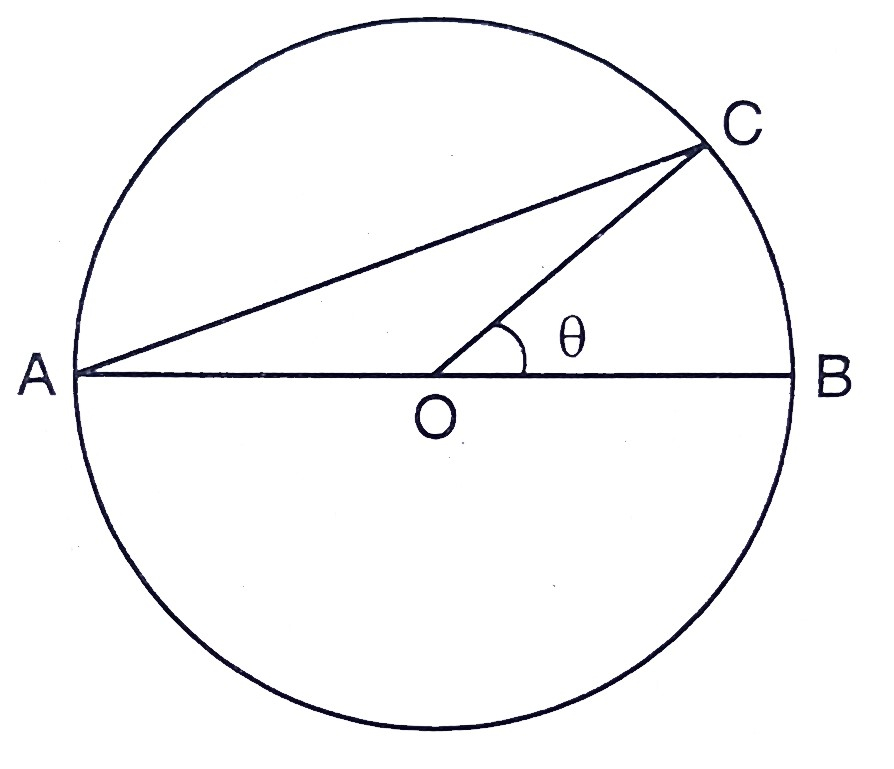
"\已知：AB是圆的直径，圆心为O。C是圆周上的一点，使得$\angle COB=\theta$。AC截取的劣弧面积等于扇形BOC面积的两倍。要求：我们必须证明$\sin \frac{\theta}{2} \cos \frac{\theta}{2}=\pi\left(\frac{1}{2}-\frac{\theta}{120}\right)$。解：设圆的半径为r。从图中，$\angle BOC=\theta$这意味着，$AOC=180^{\circ}-\theta$扇形BOC的面积=$\pi r^{2} \times \frac{\theta}{360^{\circ}}$劣弧AC的面积=扇形BOC面积的2倍=$2$… 阅读更多
"\已知：圆心为 O 的圆的半径为 \( 5 \mathrm{~cm} \)。画出两个互相垂直的半径 \( OA \) 和 \( OB \)。求解：我们要求出弦 \( AB \) 所成的弓形的面积。解：圆的半径 $r = 5\ cm$$OA$ 和 $OB$ 互相垂直。这意味着，$\angle AOB = 90^o$小弓形的面积 $=r^2(\frac{\pi \theta}{360^{\circ}}-\sin \frac{\theta}{2} \cos \frac{\theta}{2})$$=(5)^{2}(\frac{3.14 \times 90^{\circ}}{360^{\circ}}-\sin \frac{90^{\circ}}{2} \cos \frac{90^{\circ}}{2})$$=25(\frac{3.14 \times 1}{4}-\sin 45^{\circ} \cos 45^{\circ})$$=25(0.785-\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}})$$=25(0.785-\frac{1}{2})$$=25(0.785-0.5)$$=25 \times 0.285$$=7.125 \mathrm{~cm}^{2}$圆的面积 $=\pi r^{2}$$=3.14 \times(5)^{2}$$=3.14 \times 25$$=78.50 \mathrm{~cm}^{2}$因此，面积 ... 阅读更多
已知：圆的半径 $=14\ cm$。相应扇形的角度 $=60^{\circ}$。求解：我们要求出圆的小弓形的面积。解：设圆的弦为 $AB$，圆心为 $O$。在 $\Delta \mathrm{AOB}$ 中，$\mathrm{OA}=\mathrm{OB}=r$这意味着，$\Delta \mathrm{AOB}$ 是等腰三角形。设 $\angle \mathrm{OAB}=\angle \mathrm{OBA}=\theta$在 $\Delta \mathrm{OAB}$ 中，$\angle \mathrm{AOB}+\angle \mathrm{OAB}+\angle \mathrm{OBA}=180^{\circ}$$\Rightarrow 60^{\circ}+\theta+\theta=180^{\circ}$$\Rightarrow 2 \theta=120^{\circ}$$\Rightarrow \theta=60^{\circ}$因此，$\angle \mathrm{OAB}=\angle \mathrm{OBA}=60^{\circ}$这意味着，$\triangle \mathrm{AOB}$ 是等边三角形。$\mathrm{OA}=\mathrm{OB}=\mathrm{AB}=14 \mathrm{~cm}$$\Delta OAB$ 的面积 $=\frac{\sqrt{3}}{4}(14)^{2}$$=\frac{\sqrt{3}}{4} \times 196$$=49 \sqrt{3} \mathrm{~cm}^{2}$扇形 $\mathrm{OBAO}$ 的面积 $=\frac{\theta}{360^{\circ}} \times \pi r^{2} $$=\frac{22}{7} \times \frac{60^{\circ}}{360} \times 196$$=\frac{22 \times 2 \times ... 阅读更多
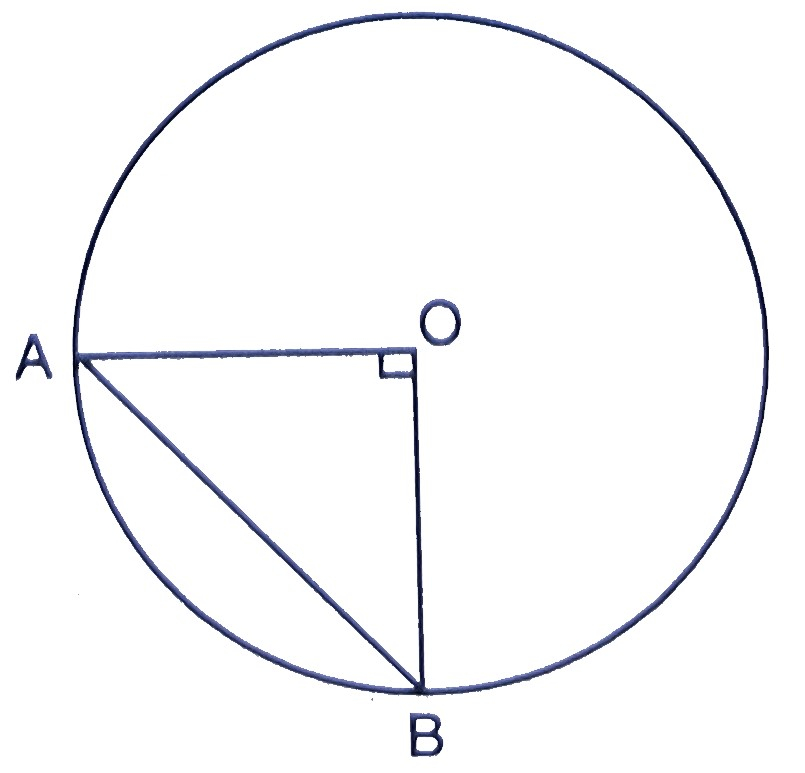
已知：半径为 \( 20 \mathrm{~cm} \) 的圆的一条弦在圆心处张成 \( 90^{\circ} \) 的角。求解：我们要求出相应大弓形的面积。解：设半径为 $10\ cm$ 的圆的弦为 $AB$，圆心为 $O$。$\angle \mathrm{AOB}=90^{\circ}$这意味着，大扇形的角度 $=360^{\circ}-90^{\circ}$$=270^{\circ}$大扇形的面积 $=\frac{270}{360} \times \pi \times(10)^{2}$$=\frac{3}{4} \times 3.14 \times 100$$=75 \times 3.14$$=235.5 \mathrm{~cm}^{2}$作 $\mathrm{OM} \perp \mathrm{AB}$$\mathrm{AM}=\frac{1}{2} \mathrm{AB}$$\angle \mathrm{AOM}=\frac{1}{2} \times 90^{\circ}$$=45^{\circ}$$\frac{\mathrm{AM}}{\mathrm{OA}}=\sin 45^{\circ}$$=\frac{1}{\sqrt{2}}$$\mathrm{AM}=10 \times \frac{1}{\sqrt{2}} \mathrm{~cm}$因此，$\mathrm{AB}=10 \sqrt{2} \mathrm{~cm}$ 和 $\mathrm{OM}=\mathrm{OA}$$\cos 45^{\circ}=10 \times \frac{1}{\sqrt{2}}$$=5 \sqrt{2} \mathrm{~cm}$$\Delta$ 的面积 ... 阅读更多
半径为 \( 14 \mathrm{~cm} \) 的圆的一条弦 \( AB \) 在圆心处张成 \( 60^{\circ} \) 的角。求圆的小弓形的面积。（使用 \( \pi=22 / 7) \)
已知：半径为 \( 14 \mathrm{~cm} \) 的圆的一条弦 \( AB \) 在圆心处张成 \( 60^{\circ} \) 的角。求解：我们要求出圆的小弓形的面积。解：圆的半径 $r = 14\ cm$圆心角 $\angle A0B = 60^o$小弓形 $\mathrm{ACB}$ 的面积 $=(\frac{\theta \pi}{360^{\circ}}-\sin \frac{\theta}{2} \cos \frac{\theta}{2}) r^2$$=(\frac{60^{\circ} \times 22}{360^{\circ} \times 7} - sin \frac{60^{\circ}}{2} \cos \frac{60^{\circ}}{2})(14)^{2}$$=196(\frac{11}{21}-\sin 30^{\circ} \cos 30^{\circ})$$=196(\frac{11}{21}-\frac{1}{2} \times \frac{\sqrt{3}}{2})$$=196(\frac{44-21 \sqrt{3}}{84})$$=\frac{196}{84}(44-21 \times 1.732)$$=\frac{7}{3}(44-36.37)$$=\frac{7}{3}(7.63)$$=17.80 \mathrm{~cm}^{2}$圆的小弓形的面积为 $17.80\ cm^2$。 阅读更多