$A B$是圆的直径，圆心为$O$。$C$是圆周上的一点，使得$\angle C O B=\theta$。由$A C$截断的小弓形的面积等于扇形$B O C$面积的两倍。证明$\sin \frac{\theta}{2} \cos \frac{\theta}{2}=\pi\left(\frac{1}{2}-\frac{\theta}{120}\right)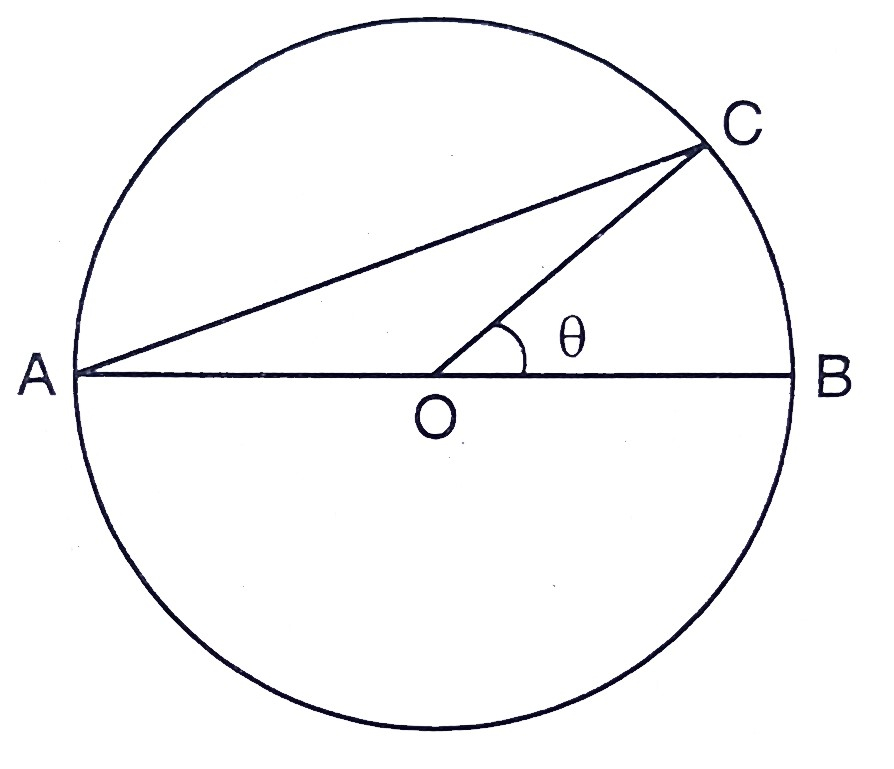$"\n

已知

$A B$是圆的直径，圆心为$O$。$C$是圆周上的一点，使得$\angle C O B=\theta$。

由$A C$截断的小弓形的面积等于扇形$B O C$面积的两倍。

要求

我们需要证明$\sin \frac{\theta}{2} \cos \frac{\theta}{2}=\pi\left(\frac{1}{2}-\frac{\theta}{120}\right)$。

解答

设圆的半径为 $r$。

从图中，

$\angle \mathrm{BOC}=\theta$

这意味着，

$\mathrm{AOC}=180^{\circ}-\theta$

扇形 $\mathrm{BOC}$ 的面积 $=\pi r^{2} \times \frac{\theta}{360^{\circ}}$

小弓形 $\mathrm{AC}$ 的面积 $=2$ (扇形 BOC 的面积)

$=2 \times \pi r^{2} \frac{\theta}{360^{\circ}}$

$=\frac{2 \pi r^{2} \theta}{360^{\circ}}$............(i)

弓形的面积 $=(\frac{\pi(180^{\circ}-\theta)}{360^{\circ}}-\sin \frac{180^{\circ}-\theta}{2} \cos \frac{180^{\circ}-\theta}{2}) r^{2}$.............(ii)

从 (i) 和 (ii) 中，我们得到，

$\frac{2 \pi r^{2} \theta}{360^{\circ}}=r^{2}(\frac{\pi(180^{\circ}-\theta)}{360^{\circ}}-\sin \frac{180^{\circ}-\theta}{2} \cos \frac{180^{\circ}-\theta}{2})$

$\Rightarrow \frac{2 \pi \theta}{360^{\circ}}=[\frac{\pi(180^{\circ}-\theta)}{360^{\circ}}-\sin (90^{\circ}-\frac{\theta}{2}) \cos (90^{\circ}-\frac{\theta}{2})]$

$\Rightarrow \frac{2 \pi \theta}{360^{\circ}}=\frac{\pi(180^{\circ}-\theta)}{360^{\circ}}-\cos \frac{\theta}{2} \sin \frac{\theta}{2}$

因此，

$\sin \frac{\theta}{2} \cos \frac{\theta}{2}=\frac{\pi(180^{\circ}-\theta)}{360^{\circ}}-\frac{2 \pi \theta}{360^{\circ}}$

$\sin \frac{\theta}{2} \cos \frac{\theta}{2}=\pi(\frac{180^{\circ}}{360^{\circ}}-\frac{\theta}{360^{\circ}}-\frac{2 \theta}{360^{\circ}})$

$\sin \frac{\theta}{2} \cos \frac{\theta}{2}=\pi(\frac{1}{2}-\frac{3 \theta}{360^{\circ}})$

$=\pi(\frac{1}{2}-\frac{\theta}{120})$

$\sin \frac{\theta}{2} \cos \frac{\theta}{2}=\pi(\frac{1}{2}-\frac{\theta}{120})$

证毕。

Tutorialspoint

更新于: 2022年10月10日

54 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习