数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学下图显示了一个圆形扇区，圆心为 O，包含一个角度 θ。证明：阴影区域的面积为 $\frac{r^{2}}{2}(\tan \theta-\frac{\pi \theta}{180})$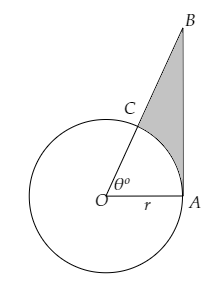
已知
一个圆形扇区，圆心为 O，包含一个角度 θ。
要求
我们必须证明阴影区域的面积为 $\frac{r^{2}}{2}(\tan \theta-\frac{\pi \theta}{180})$。
解答
从图中可以看出：
圆的半径 = r
弧 AC 在圆心处张开的角度为 θ。
∠OAB 是一个直角三角形。
在直角三角形 OAB 中：
$\tan \theta=\frac{AB}{OA}$
$\Rightarrow AB=OA \times \tan \theta$
$=r \tan \theta$
△OAB 的面积 = $\frac{1}{2} OA \times AB$
$=\frac{1}{2} \times r \times (r \tan \theta)$
$=\frac{1}{2} r^{2} \tan \theta$
扇形 OAC 的面积 = $\pi r^{2} (\frac{\theta}{360^{\circ}})$
$=\frac{\pi r^{2} \theta}{360}$
因此：
阴影部分的面积 = △OAB 的面积 - 扇形 OAC 的面积
$=\frac{1}{2} r^{2} \tan \theta-\frac{\pi r^{2} \theta}{360}$
$=\frac{1}{2} r^{2}(\tan \theta-\frac{2 \pi \theta}{360})$
$=\frac{1}{2} r^{2}(\tan \theta-\frac{\pi \theta}{180})$
$=\frac{r^{2}}{2}(\tan \theta-\frac{\pi \theta}{180})$
证毕。
更新于：2022年10月10日
43 次浏览
广告