数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究下图显示了一个半径为 r cm 的圆形扇区，包含一个 θ° 角。扇形的面积为 A cm²，扇形的周长为 50 cm。证明 θ = 360/π (25/r - 1)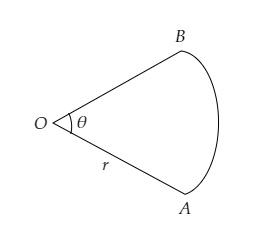
已知
一个半径为 r cm 的圆形扇区，包含一个 θ° 角。
扇形的面积为 A cm²，扇形的周长为 50 cm。
要求
我们需要证明 θ = 360/π (25/r - 1)。
解答
根据图示，
圆形扇区的半径 = r cm
中心角 = θ
扇形 OAB 的面积 = A cm²
扇形 OAB 的周长 = 50 cm
扇形的面积 = πr²(θ/360°)
⇒ A = πr²(θ/360°)
因此，
周长 = OA + 弧 AB + OB
⇒ 50 = 2r + 2πr(θ/360°)
⇒ 50 - 2r = 2πr(θ/360°)
⇒ θ/360° = (50 - 2r) / (2πr)
⇒ θ/360° = 25/(πr) - 1/π
⇒ θ/360° = 25/(πr) - 1/π
⇒ θ = 360(25/(πr) - 1/π)
⇒ θ = 360/π (25/r - 1)
证毕。
更新于：2022年10月10日
49 次浏览
广告