已知:\( ABCD \) 是边长为 \( 2 \sqrt{2} \mathrm{~cm} \) 的正方形,内接于一个圆。求解:我们需要求阴影区域的面积。解:从图中可以看出,$ABCD$ 是一个正方形。$AD = 2\sqrt2\ cm$连接 $AC$,则正方形的对角线 $\mathrm{AC}=\sqrt{2} \times \mathrm{AD}$$=\sqrt{2} \times 2\sqrt{2} \mathrm{~cm}$$=2 \times 2$$=4 \mathrm{~cm}$正方形的对角线 = 圆的直径,因此,圆的半径 $=\frac{4}{2}$$=2 \mathrm{~cm}$所以,阴影区域的面积 = 圆的面积 - 正方形的面积$=\pi r^{2}-(\mathrm{AD})^{2}$$=3.14 \times(2)^{2}-(2\sqrt{2})^{2}$$=3.14 \times 4-4\times2$$=4(3.14-2)$$=4 \times 1.14$$=4.56 \mathrm{~cm}^{2}$阴影区域的面积为 $4.56\ cm^2$。 阅读更多
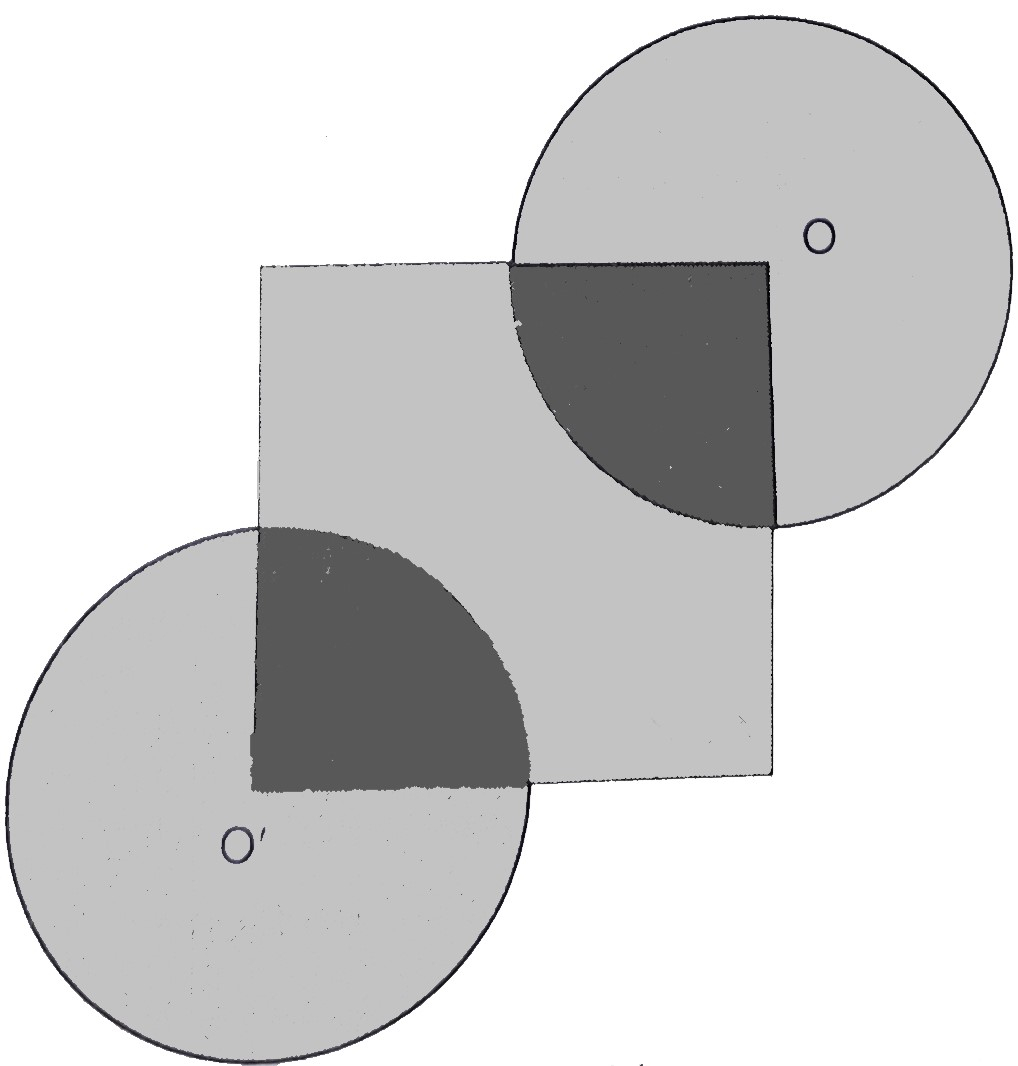
已知:正方形的边长为 \( 28 \mathrm{~cm} \),每个圆的半径是正方形边长的一半,其中 \( O \) 和 \( O^{\prime} \) 是圆心。求解:我们需要求阴影区域的面积。解:正方形的边长 $=28 \mathrm{~cm}$圆的半径 $=\frac{28}{2}$$=14 \mathrm{~cm}$因此,阴影区域的面积 = 正方形的面积 $+2\times\frac{3}{4}$ 圆的面积$=$ 正方形的面积 $+\frac{3}{2}$ 圆的面积$=(28)^{2}+\frac{3}{2} \times \frac{22}{7} \times 14^2$$=784+924$$=1708 \mathrm{~cm}^{2}$阴影区域的面积为 $1708 \mathrm{~cm}^{2}$。
已知:三角形田地的三边长分别为 \( 15 \mathrm{~m} \)、\( 16 \mathrm{~m} \) 和 \( 17 \mathrm{~m} \)。在田地的三个角上,分别用长为 \( 7 \mathrm{~m} \) 的绳子系着一头牛、一头水牛和一匹马,让它们在田地里吃草。求解:我们需要求三只动物无法吃到的田地面积。解:每个扇形的半径 $r= 7\ m$面积为 $\angle \mathrm{C}$ 的扇形区域 $=\frac{\angle \mathrm{C}}{360^{\circ}} \times \pi r^{2}$$=\frac{\angle \mathrm{C}}{360^{\circ}} \times \pi \times(7)^{2}$面积为 $\angle \mathrm{B}$ 的扇形区域 $=\frac{\angle \mathrm{B}}{360^{\circ}} \times \pi r^{2}$$=\frac{\angle \mathrm{B}}{360^{\circ}} \times \pi \times(7)^{2}$扇形区域的面积 ... 阅读更多
已知:一个数 $0.4\overline{7}$。求解:将给定数字写成 $\frac{p}{q}$ 的形式。解:设 $x=0.477777$ ...... $( i)$将 $( i)$ 乘以 $10$,$10x=4.777$ ...... $( ii)$从 $( ii)$ 减去 $( i)$,$( 10x-x)=( 4.777)-( 0.4777)$ $\Rightarrow 9x=4.3$$\Rightarrow x=\frac{4.3}{9}=\frac{43}{90}$因此,$x=\frac{43}{90}$
已知:\( 25 \times 8358 \times 4 \) \( 625 \times 3759 \times 8 \)求解:我们需要计算这些表达式的值。解:$ 25 \times 8358 \times 4 = (25 \times 4) \times 8358 = 100 \times 8358 = 835800$ $ 625 \times 3759 \times 8 = (625 \times 8) \times 3759 = (625\times2\times4)\times3759 = (1250\times4)\times3759 = 5000\times3759 = 18795000$
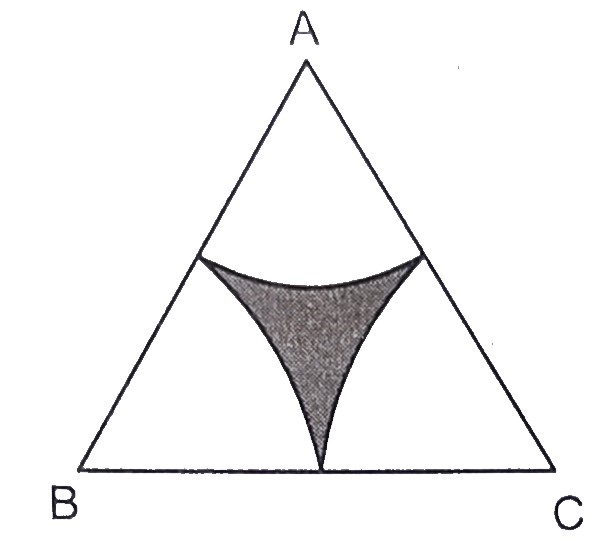
已知:\( ABC \) 是边长为 \( 8 \mathrm{~cm} \) 的等边三角形。\( A \)、\( B \) 和 \( C \) 是半径为 \( 4 \mathrm{~cm} \) 的圆弧的圆心。求解:我们需要求阴影区域的面积,精确到小数点后两位。解:$\triangle ABC$ 每条边的长度 $= 8\ cm$ 三角形的面积 $=\frac{\sqrt{3}}{4} a^{2}$$=\frac{\sqrt{3}}{4}(8)^{2}$$=\frac{1.732 \times 64}{4}$$=1.732 \times 16$$=27.712 \mathrm{~cm}^{2}$每个扇形的角度 $=60^{\circ}$ 三个扇形的面积 $=3 \times \pi r^{2} \times \frac{60^{\circ}}{360^{\circ}}$$=3 \times 3.142 \times 4 \times 4 \times \frac{1}{6}$$=1.571 \times 16$$=25.136 \mathrm{~cm}^{2}$因此,阴影区域的面积 ... 阅读更多
解:$( 9+( -6)=3)$ 已在下面的数轴上表示。
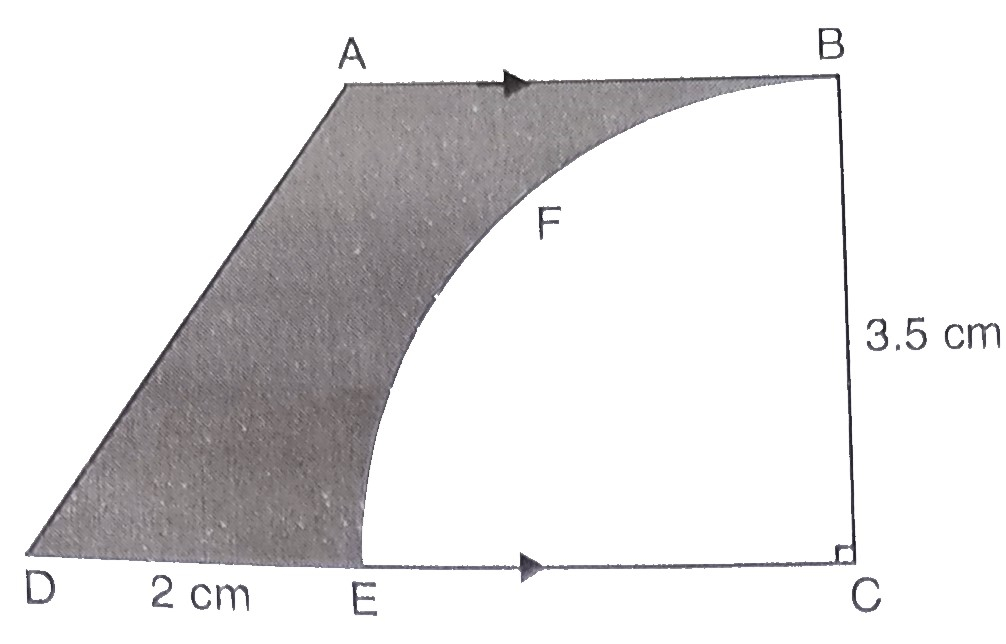
已知:\( AB \| CD \) 且 \( \angle BCD=90^{\circ} \)\( AB=BC=3.5 \) \( \mathrm{cm} \) 和 \( DE=2 \mathrm{~cm} \)求解:我们需要计算剩余金属片的面积。解:$ABCD$ 是一个梯形。$DC = DE + EC = DE + BC = 2 + 3.5 = 5.5\ cm$梯形 $ABCD$ 的面积 $= \frac{1}{2}(AB + CD) \times BC =\frac{1}{2}(3.5+5.5) \times 3.5 =\frac{1}{2} \times 9 \times 3.5 =4.5 \times 3.5 =15.75 \mathrm{~cm}^{2}$四分之一圆 $CEFB$ 的半径 $(r)=3.5 \mathrm{~cm}$四分之一圆的面积 $=\frac{1}{4} \times \pi r^{2} =\frac{1}{4} \times \frac{22}{7}(3.5)^{2} =\frac{1}{4} \times \frac{22}{7} \times 12.25 =\frac{134.75}{14} =9.6\ cm^2$因此,剩余部分的面积 ... 阅读更多
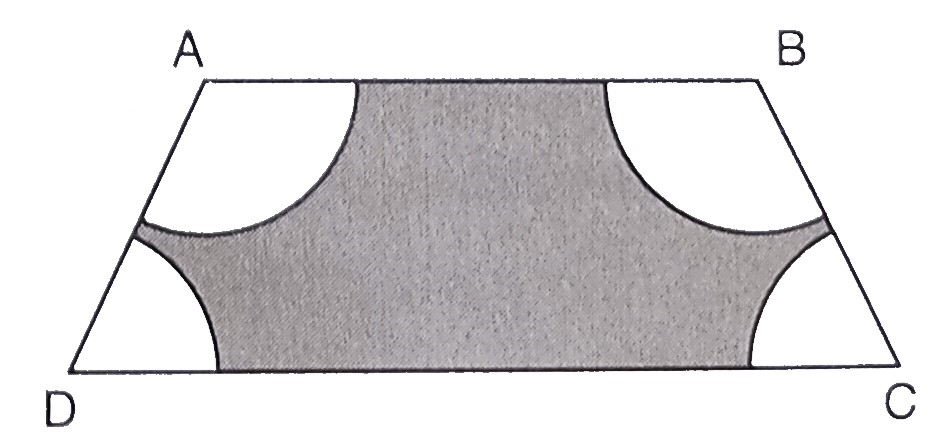
已知:ABCD是一个梯形,其中AB∥DC,AB=18厘米,DC=32厘米,AB和DC之间的距离为14厘米。已绘制以A、B、C和D为中心,半径均为7厘米的圆。要求:求图中阴影区域的面积。解:梯形每个角处的扇形半径 = 7厘米四边形的内角和 = 360°这意味着,四个扇形构成……阅读更多
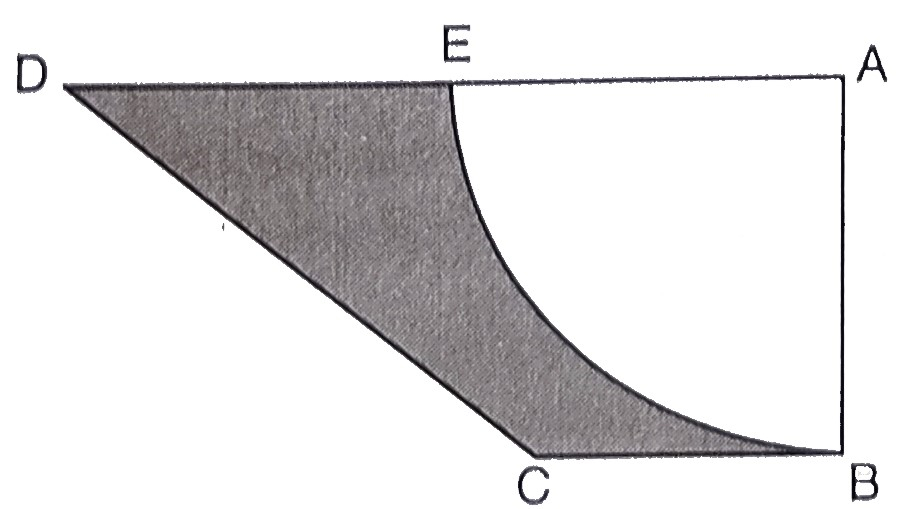
已知:ABCD是一个面积为24.5平方厘米的梯形。AD∥BC,∠DAB=90°,AD=10厘米,BC=4厘米。ABE是一个四分之一圆。要求:求阴影区域的面积。解:梯形ABCD的面积 = 1/2(AD+BC)×AB 24.5 = 1/2(10+4)h 24.5 = 7h h = 24.5/7 h = 3.5厘米这意味着,四分之一圆的半径 = 3.5 = 7/2厘米这意味着,四分之一圆的面积 = 1/4πr² = 1/4 × 22/7 × (7/2)² = 77/8 = 9.625平方厘米因此,阴影区域的面积 = 24.5 - 9.625 = 24.500 - 9.625 = 14.875平方厘米阴影区域的面积为14.875…阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP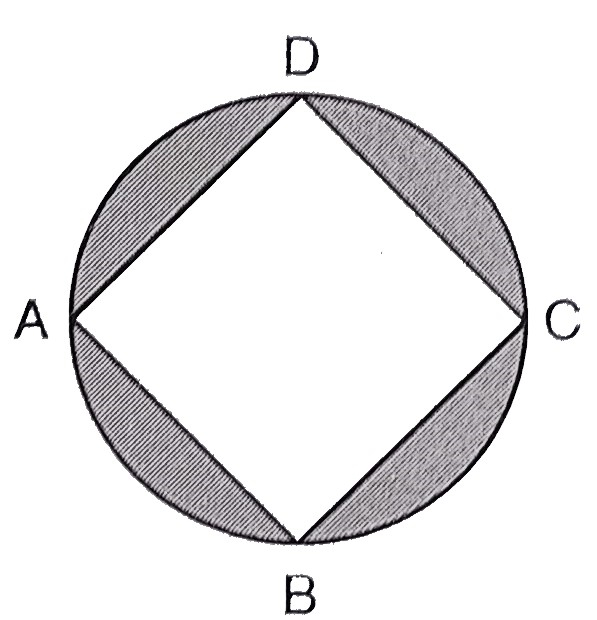 "\
"\
 "\
"\ "\
"\ "\
"\