一个三角形草地的三条边长分别为$15 \mathrm{~m}、16 \mathrm{~m}$和$17 \mathrm{~m}$。在草地的三个角上，分别用长度为$7 \mathrm{~m}$的绳子系着一头牛、一头水牛和一匹马，让它们在草地上吃草。求三只动物无法吃到的草地的面积。

已知

三角形草地的三条边长分别为$15 \mathrm{~m}、16 \mathrm{~m}$和$17 \mathrm{~m}$。

在草地的三个角上，分别用长度为$7 \mathrm{~m}$的绳子系着一头牛、一头水牛和一匹马，让它们在草地上吃草。

要求： 

求三只动物无法吃到的草地的面积。

解答

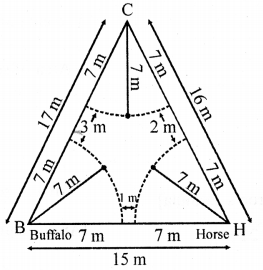
每个扇形的半径 $r= 7\ m$

以 $\angle \mathrm{C}$ 为圆心角的扇形面积 $=\frac{\angle \mathrm{C}}{360^{\circ}} \times \pi r^{2}$

$=\frac{\angle \mathrm{C}}{360^{\circ}} \times \pi \times(7)^{2}$

以 $\angle \mathrm{B}$ 为圆心角的扇形面积 $=\frac{\angle \mathrm{B}}{360^{\circ}} \times \pi r^{2}$

$=\frac{\angle \mathrm{B}}{360^{\circ}} \times \pi \times(7)^{2}$

以 $\angle \mathrm{H}$ 为圆心角的扇形面积 $=\frac{\angle \mathrm{H}}{360^{\circ}} \times \pi r^{2}$

$=\frac{\angle \mathrm{H}}{360^{\circ}} \times \pi \times(7)^{2}$
因此，

三个扇形面积之和 $=\frac{\angle \mathrm{B}}{360^{\circ}} \times \pi \times(7)^{2}+\frac{\angle \mathrm{C}}{360^{\circ}} \times \pi \times(7)^{2}+\frac{\angle \mathrm{H}}{360^{\circ}} \times \pi \times(7)^{2}$

$=\frac{(\angle \mathrm{B}+\angle \mathrm{C}+\angle \mathrm{H})}{360^{\circ}} \times \pi \times 49$

$=\frac{180^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 49$

$=11 \times 77$

$=77 \mathrm{~cm}^{2}$

$a=15, b=16$ 和 $c=17$

$s=\frac{a+b+c}{2}$

$\Rightarrow s=\frac{15+16+17}{2}$

$=\frac{48}{2}=24$

因此，

三角形草地的面积 $=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{24 \times 9 \times 8 \times 7}$

$=\sqrt{64 \times 9 \times 21}$

$=8 \times 3 \sqrt{21}$

$=24 \sqrt{21}$

三只动物无法吃到的草地的面积 = 三角形草地的面积 - 三个扇形的面积

$=24 \sqrt{21}-77 \mathrm{~m}^{2}$

三只动物无法吃到的草地的面积为 $(24 \sqrt{21}-77) \mathrm{m}^{2}$。

教程点

更新于： 2022年10月10日

486 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习