数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
"\
已知：\( BCD \)是一个半径为\( 42 \mathrm{~cm} \)的四分之一圆形。\( ABCD \)是一个正方形，\( \Delta CEF \)是一个等腰直角三角形，其相等的两条边长为\( 6 \mathrm{~cm} \)。需要求解：阴影部分的面积。解答：正方形$ABCD$的边长为 $42\ cm$，$BCD$是一个四分之一圆，$\angle BCD = 90^o$，半径 $= 42\ cm$，$\triangle CEF$是一个等腰直角三角形，$CE = CF = 6\ cm$，因此，阴影部分的面积… 阅读更多
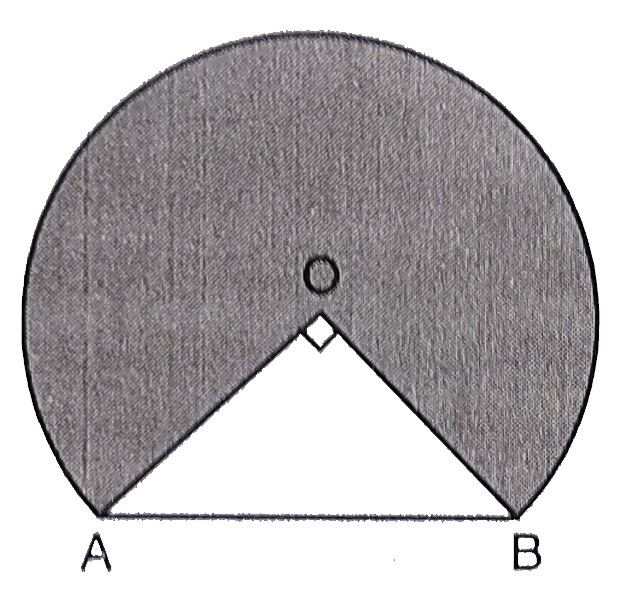
"\已知：圆形部分的半径\( OA \)为\( 2 \mathrm{~m} \)。\( \angle AOB=90^{\circ} \)。需要求解：横截面的面积。解答：隧道圆形部分的半径 $= 2\ m$，即 $OA = OB = 2\ m$ 且 $\angle AOB = 90^o$。作 $CD\ \perp\ AB$，$D$ 为 $AB$ 的中点。在直角三角形 $AOB$ 中，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{OA}^{2}+\mathrm{OB}^{2}=2^{2}+2^{2}=4+4=8$，$\Rightarrow \mathrm{AB}=\sqrt{8}=2 \sqrt{2} \mathrm{~m}$，$\mathrm{AD}=\mathrm{DB}=\frac{2\sqrt{2}}{2}=\sqrt{2}$，$\mathrm{OD}^{2}=\mathrm{OA}^{2}-\mathrm{AD}^{2}=2^{2}-(\sqrt{2})^{2}=4-2=2$，$\Rightarrow \mathrm{OD}=\sqrt{2} \mathrm{~m}$。横截面面积 $=$ 扇形 $OACB$ 的面积 $+$ $\Delta \mathrm{OAB}$ 的面积 $=\frac{3}{4} \pi r^{2}+\frac{1}{2} \times \mathrm{OA} \times \mathrm{OB}=\frac{3}{4} \pi \times(2)^{2}+\frac{1}{2} \times 2 \times 2=(3 \pi+2) … 阅读更多
已知：圆形部分的半径\( OA \)为\( 2 \mathrm{~m} \)。\( \angle AOB=90^{\circ} \)。需要求解：横截面的周长。解答：隧道圆形部分的半径 $= 2\ m$，即 $OA = OB = 2\ m$ 且 $\angle AOB = 90^o$。作 $CD\ \perp\ AB$，$D$ 为 $AB$ 的中点。在直角三角形 $AOB$ 中，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{OA}^{2}+\mathrm{OB}^{2}=2^{2}+2^{2}=4+4=8$，$\Rightarrow \mathrm{AB}=\sqrt{8}=2 \sqrt{2} \mathrm{~m}$，$\mathrm{AD}=\mathrm{DB}=\frac{2\sqrt{2}}{2}=\sqrt{2}$，$\mathrm{OD}^{2}=\mathrm{OA}^{2}-\mathrm{AD}^{2}=2^{2}-(\sqrt{2})^{2}=4-2=2$，$\Rightarrow \mathrm{OD}=\sqrt{2} \mathrm{~m}$。大圆弧 $ACB$ 的长度 $=2 \pi r \times \frac{3}{4} =2 \times \pi \times 2 \times \frac{3}{4}=3 \pi$。因此，横截面的总周长 = … 阅读更多
"\已知：圆形部分的半径\( OA \)为\( 2 \mathrm{~m} \)。\( \angle AOB=90^{\circ} \)。需要求解：隧道的髙度。解答：隧道圆形部分的半径 $= 2\ m$，即 $OA = OB = 2\ m$ 且 $\angle AOB = 90^o$。作 $CD\ \perp\ AB$，$D$ 为 $AB$ 的中点。在直角三角形 $AOB$ 中，根据勾股定理，$\mathrm{AB}^{2}=\mathrm{OA}^{2}+\mathrm{OB}^{2}=2^{2}+2^{2}=4+4=8$，$\Rightarrow \mathrm{AB}=\sqrt{8}=2 \sqrt{2} \mathrm{~m}$，$\mathrm{AD}=\mathrm{DB}=\frac{2\sqrt{2}}{2}=\sqrt{2}$，$\mathrm{OD}^{2}=\mathrm{OA}^{2}-\mathrm{AD}^{2}=2^{2}-(\sqrt{2})^{2}=4-2=2$，$\Rightarrow \mathrm{OD}=\sqrt{2} \mathrm{~m}$。隧道的髙度 $=\mathrm{CD}=\mathrm{OC}+\mathrm{OD}=(2+\sqrt{2}) \mathrm{m}$。隧道的髙度为 $(2+\sqrt{2}) \mathrm{m}$。 阅读更多
"\已知：\( ABC \)是一个直角三角形，其中\( \angle A=90^{\circ}, AB=21 \mathrm{~cm} \)和\( AC=28 \mathrm{~cm} \)。在\( AB, BC \)和\( AC \)上分别以它们为直径作半圆。需要求解：阴影部分的面积。解答：在直角三角形 $ABC$ 中，根据勾股定理，$BC^2 = AB^2+AC^2= 21^2+ 28^2= 441 + 784= 1225=(35)^2$，$\Rightarrow BC = 35\ cm$。最大半圆的半径 $R = \frac{35}{2}\ cm$，$AB$ 上半圆的半径 $=\frac{21}{2}\ cm$，$AC$ 上半圆的半径 $=\frac{28}{2}=… 阅读更多
"\已知：\( AB=36 \mathrm{~cm} \)，\( M \)是\( AB \)的中点。在\( AB, AM \)和\( MB \)上分别以它们为直径作半圆。一个以\( C \)为圆心的圆与这三个半圆相切。需要求解：阴影部分的面积。解答：最大半圆的直径 $= 36\ cm$，半径 $R =\frac{36}{2}= 18\ cm$。每个较小半圆的直径 $= 18\ cm$，半径 $r_{1}=\frac{18}{2}=9 \mathrm{~cm}$。最小圆的直径 $=\frac{1}{3} \times 36=12 \mathrm{~cm}$，半径 $r_{2}=\frac{12}{2}=6 \mathrm{~cm}$。因此，阴影部分的面积 = … 阅读更多
题目：求用一个长10厘米、宽6厘米、高9厘米的长方体可以制作出多少个边长为3厘米的小正方体。解答：长方体的尺寸 = 10厘米 × 6厘米 × 9厘米正方体的体积 = 边长³ = 3³ = 27 立方厘米长方体的体积 = 长 × 宽 × 高 正方体个数 × 正方体体积 = 长方体体积 ⇒ 正方体个数 × 27 = (10 × 6 × 9) ⇒ 正方体个数 = 10 × 6 × 9/27 = 20 因此，正方体个数为20个。
已知：一个半径为r的球体熔化后重新铸造成一个高为h的圆锥体。题目：求该圆锥体底部的半径。解答：如题所示，一个半径为r的球体熔化后重新铸造成一个高为h的圆锥体。设新形成的圆锥体的半径为R。因此，球体的体积 = (4/3)πr³ 圆锥体的体积 = (1/3)πR²h 我们知道，球体的体积 = 圆锥体的体积 ⇒ (4/3)πr³ = (1/3)πR²h ⇒ 4r³ = R²h ⇒ R² = 4r³/h ⇒ R = √(4r³/h) ⇒ R = 2√(r³/h) 因此，圆锥体的半径为 2√(r³/h)。阅读更多
已知：一个正方体的每条棱都增加50%。题目：求正方体表面积的百分比增加。解答：设正方体的边长为a。正方体的表面积 = 6a² 增加50%后，新的边长 = (3/2)a新的表面积 = 6((3/2)a)² = 6 × (9/4)a² = (27/2)a²表面积的增加量 = (27/2)a² - 6a² = (27 - 12)/2 a² = (15/2)a²表面积增加的百分比 = (表面积增加量 / 原表面积) × 100 = ((15/2)a² / 6a²) × 100 = 15/(2 × 6) × 100 = 1.25 × 100 = 125%
已知：一个正方体的对角线长度为3√3米。题目：求该正方体的体积。解答：对角线长度 = √3 × 边长 ⇒ 3√3 = √3 × 边长 ⇒ 边长 = 3体积 = 3³ = 27 立方米 因此，正方体的体积为27立方米。