下图显示了铁路隧道的横截面。圆形部分的半径OA为2米。如果∠AOB=90°，计算横截面的面积。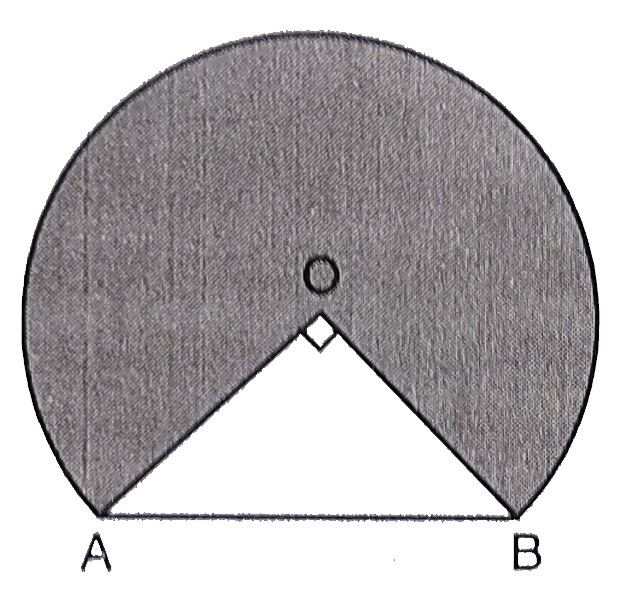

已知

圆形部分的半径OA为2米。

∠AOB=90°。

要求：

我们必须找到横截面的面积。

解答

隧道圆形部分的半径 = 2米

这意味着：

OA = OB = 2米，∠AOB = 90°

作CD ⊥ AB

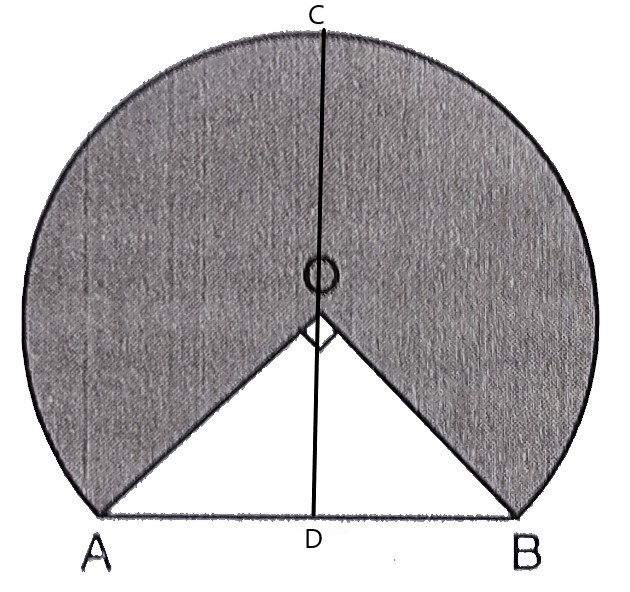
D是AB的中点

在直角三角形AOB中，根据勾股定理：

AB² = OA² + OB²

$=2^{2}+2^{2}$

$=4+4$

$=8$

=> AB = √8

= √(4 × 2)

= 2√2 米

AD = DB = (2√2)/2 = √2

OD² = OA² - AD²

= 2² - (√2)²

$=4-2$

$=2$

=> OD = √2 米

横截面面积 = 扇形OACB面积 + 三角形OAB面积

= (3/4)πr² + (1/2) × OA × OB

= (3/4)π × 2² + (1/2) × 2 × 2

= (3π + 2) 平方米

横截面的面积为(3π + 2)平方米。

教程点

更新于：2022年10月10日

62 次浏览

开启你的职业生涯

完成课程获得认证

开始学习