数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学
正确答案是选项 (2) 无限。当两块平面镜彼此平行（即以 0° 角对齐）时，会形成放置在它们之间的物体的无限多个图像。
已知：长方体的表面积为 1372 平方厘米。它的尺寸之比为 4:2:1。求解：我们需要求出它的长度。解：设长方体的长、宽、高分别为 $4x, 2x$ 和 $x$。长方体的表面积公式为 $2(lb+bh+lh)$。因此，$2[(4x)(2x)+(2x)(x)+(4x)(x)]=1372$$8x^2+2x^2+4x^2=\frac{1372}{2}$$14x^2=686$$x^2=\frac{686}{14}$$x^2=49$$x=\sqrt{49}$$x=7\ cm$$\Rightarrow 4x=4(7)\ cm=28\ cm$长方体的长度为 28 厘米。
已知：Shubham 买了一些巧克力，并把其中一半给了 Saurabh。Saurabh 买了一些糖果，并把其中一半给了 Shubham。Shubham 吃了 12 块糖果，Saurabh 吃了 18 块巧克力。之后，Shubham 的糖果和巧克力的数量之比为 1:7，Saurabh 的糖果和巧克力的数量之比为 1:4。求解：我们需要求出 Saurabh 买糖果的数量。解：设 Shubham 买巧克力的数量为 2x，Saurabh 买糖果的数量为 2y。Shubham 剩下的糖果数量 = y-12 Shubham 剩下的巧克力数量 =… 阅读更多
电镀电解用于电镀物体（用一层薄金属覆盖它们），这对于用更昂贵的金属（如铜或银）覆盖更便宜的金属非常有用，以防止腐蚀，使物体看起来有光泽并耐刮擦。工作原理 1. 负电极（或阴极）应该是要电镀的物体。（这里选择铜勺）2. 正电极（或阳极）应该是你想要用来覆盖物体的金属。（这里选择银）3. 电解质应该是镀层金属盐的溶液，例如它的金属… 阅读更多
已知：$PQ=1.28\ cm, PR=2.56\ cm, PM=0.16\ cm$ 和 $PN=0.32\ cm$。求解：我们需要判断 $MN\parallel QR$ 是否成立。解：我们知道，如果一条直线将三角形的两边按比例分割，则它平行于第三边。$QM=PQ-PM=(1.28-0.16)\ cm=1.12\ cm$$NR=PR-PN=(2.56-0.32)\ cm=2.24\ cm$因此，$\frac{PM}{QM}=\frac{0.16}{1.12}=\frac{0.16\times100}{1.12\times100}=\frac{16}{112}=\frac{1}{7}$$\frac{PN}{NR}=\frac{0.32}{2.24}=\frac{0.32\times100}{2.24\times100}=\frac{32}{224}=\frac{1}{7}$$\frac{PM}{QM}=\frac{PN}{NR}$因此，根据比例定理的逆定理，$MN$ 平行于 $QR$。
已知：在三条线段 $OA, OB$ 和 $OC$ 中，分别选择点 $L, M, N$ 使得 $LM \parallel AB$ 和 $MN \parallel BC$，但 $L, M, N$ 和 $A, B, C$ 中的点都不共线。求解：我们需要证明 $LN \parallel AC$。证明：根据图示，$LM \parallel AB$ 和 $MN \parallel BC$因此，根据基本比例定理，在 $\triangle OAB$ 中，$\frac{OL}{AL}=\frac{OM}{MB}$....(i)$\frac{ON}{NC}=\frac{OM}{MB}$....(ii)由公式 (i) 和 (ii)，我们得到，$\frac{OL}{AL}=\frac{ON}{NC}$因此，根据基本比例定理的逆定理，$LN \parallel AC$。证毕。 阅读更多
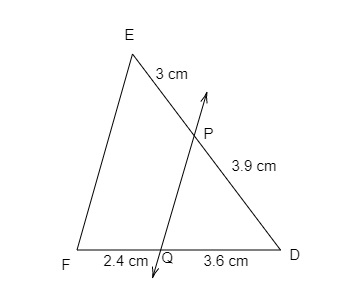
"\已知：$DP=3.9\ cm, PE=3\ cm, DQ=3.6\ cm$ 和 $QF=2.4\ cm$。求解：我们需要判断 $PQ\parallel EF$ 是否成立。解：我们知道，如果一条直线将三角形的两边按比例分割，则它平行于第三边。因此，$\frac{DP}{PE}=\frac{3.9}{3}=1.3$$\frac{DQ}{QF}=\frac{3.6}{2.4}=\frac{3}{2}=1.5$$\frac{DP}{PE}≠\frac{DQ}{QF}$因此，$PQ$ 不平行于 $EF$。
已知：$PM=4\ cm, QM=4.5\ cm, PN=4\ cm$ 和 $NR=4.5\ cm$。求解：我们需要判断 $MN\parallel QR$ 是否成立。解：我们知道，如果一条直线将三角形的两边按比例分割，则它平行于第三边。因此，$\frac{PM}{QM}=\frac{4}{4.5}=\frac{4\times2}{4.5\times2}=\frac{8}{9}$$\frac{PN}{NR}=\frac{4}{4.5}=\frac{4\times2}{4.5\times2}=\frac{8}{9}$$\frac{PM}{QM}=\frac{PN}{NR}$因此，根据比例定理的逆定理，$MN$ 平行于 $QR$。
"\图中所示的运动类型是：-(a) 水龙头 - 转动。(b) 火车 - 平动。(c) 跷跷板 - 振动。(d) 摩天轮 - 转动。解释1. 转动 - 当物体绕其固定轴旋转（或自转）时，称为转动或旋转运动。2. 平动 - 物体沿直线（直线或曲线）移动而没有任何旋转的运动类型称为平动。3. 振动 - 物体围绕一个固定点来回移动的运动类型称为振动运动。阅读更多