数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：数$\sqrt{2}$和$\sqrt{3}$。求解：在$\sqrt{2}$和$\sqrt{3}$之间找到一个有理数。解：已知两个数$a$和$b$之间的有理数为$\frac{a+b}{2}$。$\sqrt{2}$和$\sqrt{3}$之间的有理数=$\frac{\sqrt{2}+\sqrt{3}}{2}=\frac{1.414+1.732}{2}$ =1.5 =$\frac{15}{10}$ =$\frac{3}{2}$ $\sqrt{2}$和$\sqrt{3}$之间的有理数为$\frac{3}{2}$。
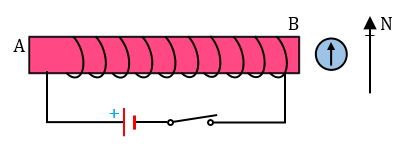
"\按下开关时，(a)电流将在A端沿顺时针方向流动，因为它具有正极，因此该端将表现为南极。(b)由于A端表现为南极，则线圈的另一端B将表现为北极，并且由于北极的排斥力，指南针（或指南针的指针）将远离线圈移动。图片中的额外信息仅供参考 电磁铁的南北极性可以通过…… 阅读更多
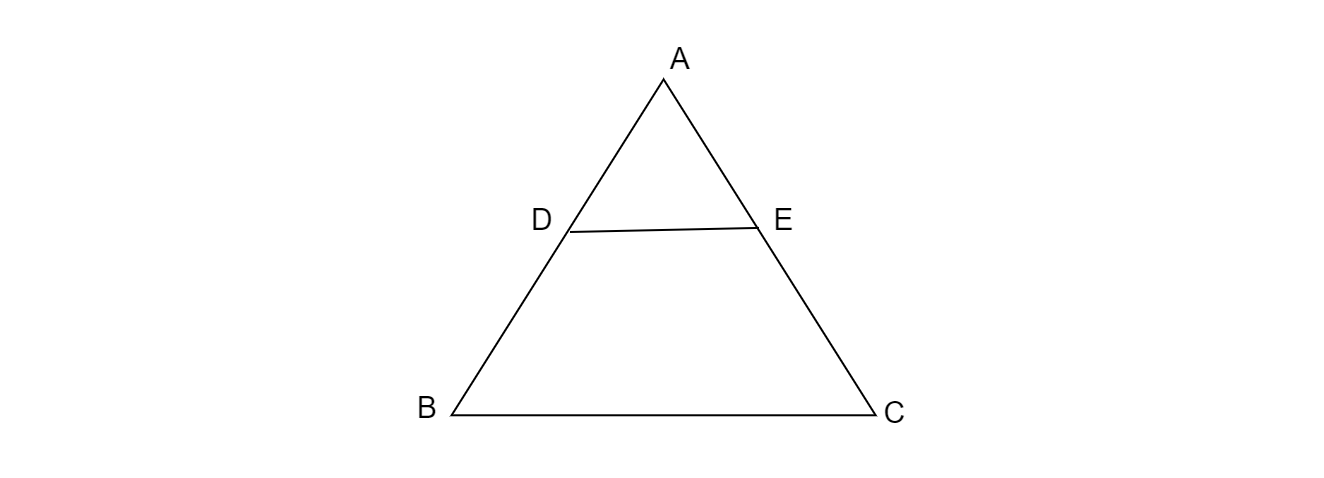
"\已知：$\vartriangle ABC$，其中$DE∥BC, AD=1\ cm, BD=2\ cm$。求解：求$ar( \vartriangle ABC)$与$ar( \vartriangle ADE)$的比率。解：在$\vartriangle ABC$和$\vartriangle ADE$中，$\angle A=\angle A$（公共角）$\angle ABC=\angle ADE$（因为$DE∥BC$)$\angle ACB=\angle AED$（因为$DE∥BC$)$\therefore \vartriangle ABC~\vartriangle ADE$（AAA规则）$\Rightarrow\frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{AB}{AD})^{2}$$\Rightarrow \frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{AD+BD}{AD})^{2}$$\Rightarrow \frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{1+2}{1})^{2}$$\Rightarrow \frac{ar( \vartriangle ... 阅读更多
已知通电直导线垂直放置。如果电流沿垂直向上方向通过该导线，则它产生的磁场将沿逆时针方向。麦克斯韦右手螺旋定则用于查找磁场的方向。 解释根据麦克斯韦右手螺旋定则，当将通电导体握在右手，使拇指指向电流方向时，缠绕导体的指头给出导线周围磁力线的方向。当拇指向上时，…… 阅读更多
已知：方程$x^{2}+4x+k=0$。求解：求k的值，使给定方程具有相等的根。解：给定方程$x^{2}+4x+k=0$。将其与标准方程$ax^{2}+bx+c=0$比较，得到$a=1,\ b=4$和$c=k$。其判别式$D=b^{2}-4ac$ $=4^{2}-4×1×k$ $=16-4k$。对于实根，$D≥0$ $\Rightarrow 16-4k≥0$ $\Rightarrow 4k≤16$ $\Rightarrow k≤\frac{16}{4}$ $\Rightarrow k≤4$。对于$k≤4$，给定的二次方程将具有实根。
已知：方程$3x^{2}– 10x+k=0$。求解：求k的值，使方程的根互为倒数。解：给定方程：$3x^{2}-10x+k=0$。将其与$ax^{2}+bx+c=0$比较，我们有$a=3,\ b=-10,\ c=k$。设$\alpha$和$\frac{1}{\alpha}$是给定二次方程的根。根的乘积=$\frac{c}{a}$$\alpha.\frac{1}{\alpha}=\frac{k}{3}$$\Rightarrow\frac{k}{3}=1$$\Rightarrow k=3$。因此，对于$k=3$，给定方程将具有互为倒数的根。
已知：$tan2A=cot( A-24^{o})$。求解：求A的值。解：$tan2A=cot( A-24^{o})$ $\Rightarrow tan 2A = tan[90^{o}-( A-24^{o})]$ $\Rightarrow tan 2A = tan( 90^{o}-A+24^{o})$ $\Rightarrow tan 2A = tan( 114^{o}- A)$ $\Rightarrow 2A =114^{o}-A$ $\Rightarrow 3A=114^{o}$ $\Rightarrow A=38^{o}$
已知：$( sin^{2}33^{o} + sin^{2}57^{o})$。求解：求其值。解：$sin^{2}33^{o} + sin^{2}57^{o}$=$sin^{2}33^{o}+cos^{2}(90^{o} -57^{o})$=$sin^{2}33^{o}+cos^{2}33^{o}$ =1
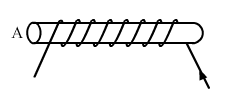
"\螺线管的A端将是南极（S极），因为在这个端电流沿顺时针方向流动。图片中的额外信息仅供参考可以使用钟面规则轻松找到电磁铁的南北极性，因为根据该规则，“当观察者发现电流在一个线圈面上沿逆时针方向流动时，该线圈面将表现为北极。而如果观察者发现电流沿顺时针方向流动，则该线圈面将…… 阅读更多
已知：AB 是圆的直径，圆心坐标为 (2, -3)，点 B 的坐标为 (1, 4)。 求：点 A 的坐标。 解：设圆心为 O，点 A 的坐标为 (x, y)。 因为 AB 是圆的直径，所以 O 是 AB 的中点。 已知两点 (x₁, y₁) 和 (x₂, y₂)，则中点坐标为 ($\frac{x₁+x₂}{2}$, $\frac{y₁+y₂}{2}$) 。根据中点公式，(2, -3) = ($\frac{x+1}{2}$, $\frac{y+4}{2}$) $\Rightarrow \frac{x+1}{2}=2$ 且 $\frac{y+4}{2}=-3$ $\Rightarrow x+1=4$ 且 $y+4=-3$ $\Rightarrow x=4-1$ 且 ... 阅读更多