Loading [MathJax]/jax/element/mml/optable/GeneralPunctuation.js

如图1所示， $DE||BC$ ， $AD=1\ cm$ ， $BD=2\ cm$ 。 $\vartriangle ABC$ 的面积与 $\vartriangle ADE$ 的面积之比是多少？

学术数学 NCERT 10年级

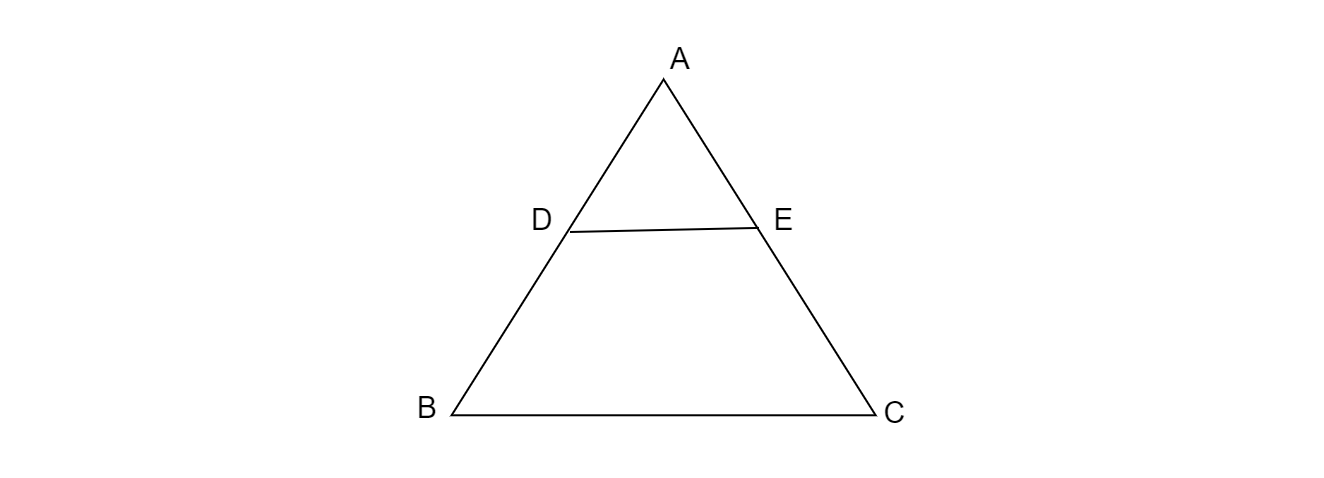
已知：

$\vartriangle ABC$ ，其中

$DE∥BC, AD=1\ cm, BD=2\ cm$

求解：求

$\vartriangle ABC$ 的面积与

$\vartriangle ADE$ 面积的比值。

解答

在

$\vartriangle ABC$ 和

$\vartriangle ADE$ 中，

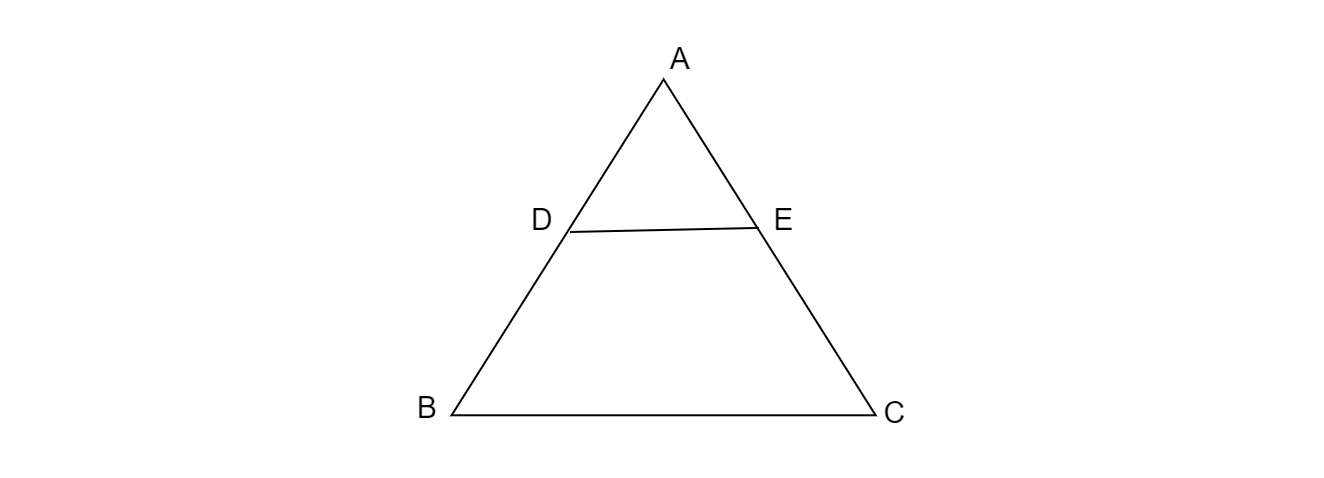
$\angle A=\angle A$ (公共角)

$\angle ABC=\angle ADE$ (

$\because DE∥BC$ )

$\angle ACB=\angle AED$ (

$\because DE∥BC$ )

$\therefore \vartriangle ABC~\vartriangle ADE$ (AAA相似)

$\Rightarrow\frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{AB}{AD})^{2}$

$\Rightarrow \frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{AD+BD}{AD})^{2}$

$\Rightarrow \frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{AD+BD}{AD})^{2}$

$\Rightarrow \frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{1+2}{1})^{2}$

$\Rightarrow \frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=(\frac{3}{1})^{2}$

$\Rightarrow \frac{ar( \vartriangle ABC)}{ar( \vartriangle ADE)}=\frac{9}{1}$

$\therefore$ ，

$\vartriangle ABC$ 和

$\vartriangle ADE$ 的面积比为

$9:1$

Tutorialspoint

更新于：2022年10月10日

浏览量：40

开启你的职业生涯

完成课程获得认证

广告