数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究如图4所示，三角形ABC外接一个半径为3厘米的圆，线段BD和DC的长度分别为6厘米和9厘米。如果三角形ABC的面积为54平方厘米，则求边AB和AC的长度。
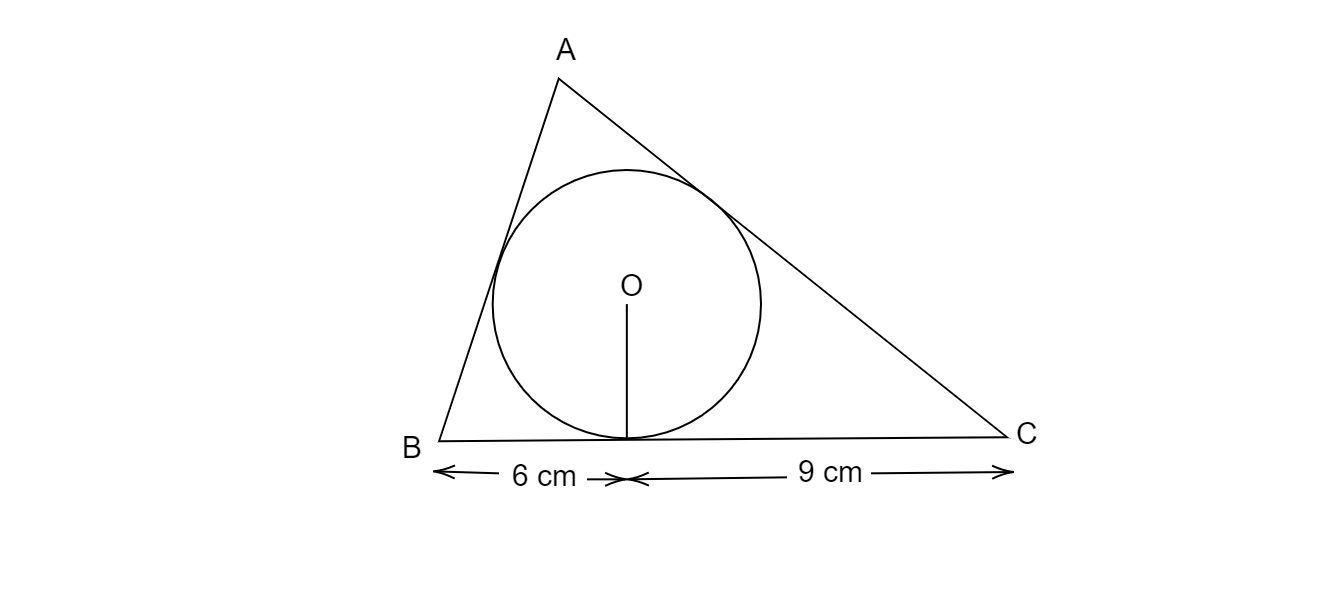
已知：三角形ABC外接一个半径为3厘米的圆，线段BD和DC的长度分别为6厘米和9厘米。三角形ABC的面积为54平方厘米。
求解：求边AB和AC的长度。
解
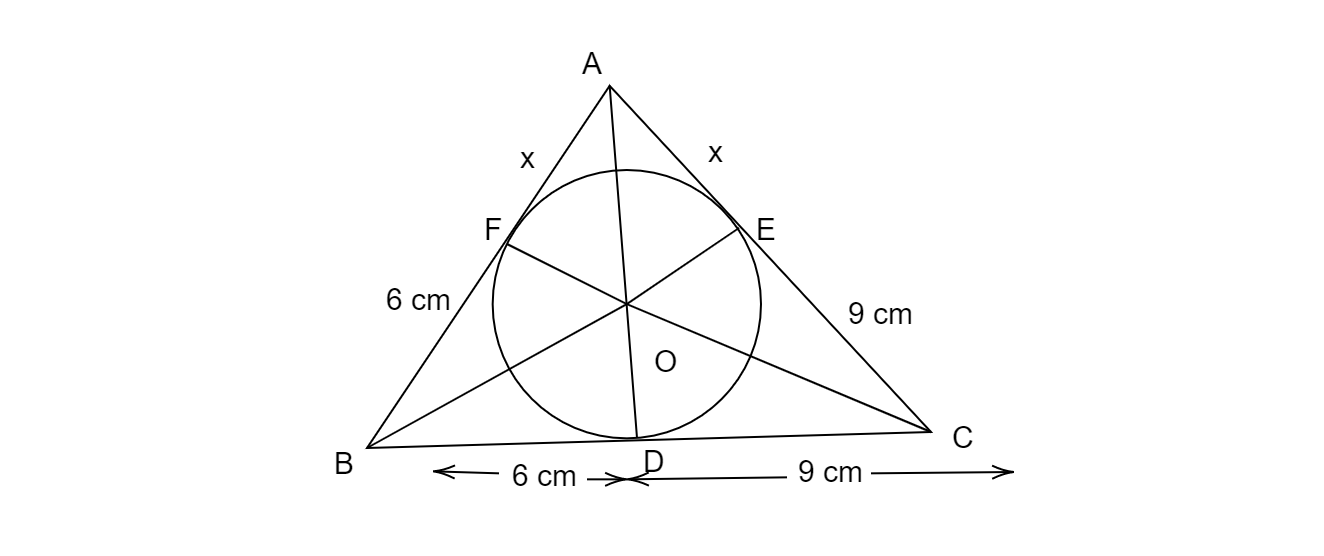
设圆与三角形AB和AC的切点分别为F和E。
设线段AF的长度为x。
现在，可以观察到
BF = BD = 6厘米 (B点引出的切线)
CE = CD = 9厘米 (C点引出的切线)
AE = AF = x (A点引出的切线)
AB = AF + FB = x + 6
BC = BD + DC = 6 + 9 = 15
CA = CE + EA = 9 + x
2s = AB + BC + CA = x + 6 + 15 + 9 + x = 30 + 2x = 2(15 + x)
s = 15 + x
s – a = 15 + x – 15 = x
s – b = 15 + x – (x + 9) = 6
s – c = 15 + x – (6 + x) = 9
三角形ABC的面积为：
√[s(s-a)(s-b)(s-c)]
=> 54 = √[(15 + x) * x * 6 * 9]
=> 54 = 3√[6(x² + 15x)]
=> √[6(x² + 15x)] = 54/3 = 18
=> 6(x² + 15x) = 324
=> x² + 15x = 54
=> x² + 15x - 54 = 0
=> x² + 18x - 3x - 54 = 0
=> x(x + 18) - 3(x + 18) = 0
=> (x - 3)(x + 18) = 0
如果 x - 3 = 0
=> x = 3
如果 x + 18 = 0
=> x = -18
因为长度不能为负数，所以我们舍去x = -18。
∴ x = 3
∴ AB = x + 6 = 3 + 6 = 9厘米
且 AC = x + 9 = 3 + 9 = 12厘米
因此，边AB的长度为9厘米，边AC的长度为12厘米。
更新于：2022年10月10日
48次浏览
广告