作图：已知$BC = 7.5\ cm$，$AC = 5\ cm$，$\angle C = 60^{\circ}$，构造三角形$∆ABC$。
待办事项：构造三角形$∆ABC$，其中$BC = 7.5\ cm$，$AC = 5\ cm$，$m \angle C = 60^{\circ}$。
作图步骤
- 让我们画一条线段$BC$，长度为$7.5\ cm$。
- 从点$C$出发，画一条射线$CX$，使它与$BC$的夹角为$60^{\circ}$，即$\angle ACB=60^{\circ}$。
- 以$C$为圆心，画一个半径为$5\ cm$的圆弧，该圆弧与$CX$相交于点$A$。
- 现在，连接$AB$，得到所需的三角形。
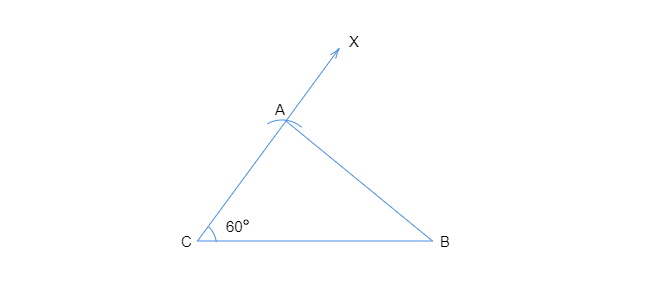
$\triangle ABC$ 是所求的三角形。
因此，构造完成！
- 相关文章
- 作图：在$∆ABC$中，$BC = 3.6\ cm, AB + AC = 4.8\ cm$，且$\angle B = 60^o$。
- 仅使用直尺和圆规，作图：已知$∆ABC$，底边$BC = 7\ cm, \angle ABC = 60^o$，且$AB + AC = 12\ cm$。
- 作图：构造$∆ABC$，使得$AB=2.5\ cm$，$BC=6\ cm$，$AC=6.5\ cm$。测量$\angle B$。
- 作图：构造$∆ABC$，已知$m\angle A = 60^{\circ}$，$m\angle B = 30^{\circ}$，且$AB = 5.8\ cm$。
- 作图：构造$∆ABC$，其中$AB + AC = 5.6\ cm, BC = 4.5\ cm$，且$\angle B = 45^o$。
- ∆ABC ~ ∆LMN。在∆ABC中，AB = 5.5 cm，BC = 6 cm，CA = 4.5 cm。构造∆ABC和∆LMN，使得$\frac{BC}{MN} \ =\ \frac{5}{4}$。
- 作图：构造$∆DEF$，使得$DE = 5\ cm$，$DF = 3\ cm$，且$\angle EDF = 90^{\circ}$。
- 作图：构造$\vartriangle ABC$，其中$BC=7\ cm,\ \angle B=75^{o}$，且$AB+AC=12\ cm$。
- 作图：构造$\triangle ABC$，其中$BC = 3.4\ cm, AB - AC = 1.5\ cm$，且$\angle B = 45^o$。
- 作图：构造一个三角形\( \mathrm{ABC} \)，其中\( \mathrm{BC}=7 \mathrm{~cm}, \angle \mathrm{B}=75^{\circ} \)，且\( \mathrm{AB}+\mathrm{AC}=13 \mathrm{~cm} \)。
- 作图：构造一个三角形\( \mathrm{ABC} \)，其中\( \mathrm{BC}=8 \mathrm{~cm}, \angle \mathrm{B}=45^{\circ} \)，且\( \mathrm{AB}-\mathrm{AC}=3.5 \mathrm{~cm} \)。
- 作图：构造一个等腰直角三角形$ABC$，其中$m\angle ACB = 90^{\circ}$，且$AC = 6\ cm$。
- 选择正确的答案并说明理由：在$∆ABC$中，$AB = 6\sqrt3\ cm, AC = 12\ cm$，且$BC = 6\ cm$。角B为：（a）$120^o$（b）$60^o$（c）$90^o$（d）$45^o$
- 作图：如果$PQ = 5\ cm$，$m\angle\ PQR = 105^{\circ}$，且$m\angle QRP = 40^{\circ}$，则构造$∆PQR$。[提示：回顾三角形内角和性质。]
- 作图：构造一个与\( \triangle A B C \)相似的三角形，其中\( A B=4.6 \mathrm{~cm}, \mathrm{BC}=5.1 \mathrm{~cm}, \angle A=60^{\circ} \)，比例因子为\( 4: 5 \)。
数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究