
- Java 数据结构与算法 教程
- Java 数据结构与算法 - 首页
- Java 数据结构与算法 - 概述
- Java 数据结构与算法 - 环境搭建
- Java 数据结构与算法 - 算法
- Java 数据结构与算法 - 数据结构
- Java 数据结构与算法 - 数组
- Java 数据结构与算法 - 链表
- Java 数据结构与算法 - 双向链表
- Java 数据结构与算法 - 循环链表
- Java 数据结构与算法 - 栈
- 数据结构与算法 - 表达式解析
- Java 数据结构与算法 - 队列
- Java 数据结构与算法 - 优先队列
- Java 数据结构与算法 - 树
- Java 数据结构与算法 - 哈希表
- Java 数据结构与算法 - 堆
- Java 数据结构与算法 - 图
- Java 数据结构与算法 - 搜索技术
- Java 数据结构与算法 - 排序技术
- Java 数据结构与算法 - 递归
- Java 数据结构与算法 - 有用资源
- Java 数据结构与算法 - 快速指南
- Java 数据结构与算法 - 有用资源
- Java 数据结构与算法 - 讨论
Java 数据结构与算法 - 快速指南
Java 数据结构与算法 - 概述
什么是数据结构?
数据结构是以一种有效的方式组织数据的方法。以下术语是数据结构的基础术语。
接口 - 每个数据结构都有一个接口。接口表示数据结构支持的一组操作。接口只提供支持的操作列表、它们可以接受的参数类型以及这些操作的返回类型。
实现 - 实现提供数据结构的内部表示。实现还提供数据结构操作中使用的算法的定义。
数据结构的特性
正确性 - 数据结构的实现应该正确地实现其接口。
时间复杂度 - 数据结构操作的运行时间或执行时间必须尽可能短。
空间复杂度 - 数据结构操作的内存使用量应尽可能少。
数据结构的必要性
随着应用程序变得越来越复杂和数据丰富,如今应用程序面临三个常见问题。
数据搜索 - 考虑一家商店有 100 万 (106) 件商品的库存。如果应用程序要搜索一件商品,则每次都必须在 100 万 (106) 件商品中搜索商品,从而减慢搜索速度。随着数据增长,搜索会变得更慢。
处理器速度 - 尽管处理器速度非常高,但如果数据增长到数十亿条记录,则会受到限制。
多个请求 - 由于数千个用户可以同时在 Web 服务器上搜索数据,即使是非常快速的服务器在搜索数据时也会失败。
为了解决上述问题,数据结构可以提供帮助。数据可以以这样一种方式组织在数据结构中,使得可能不需要搜索所有项目,并且可以几乎立即搜索所需的数据。
执行时间情况
通常使用三种情况来相对地比较各种数据结构的执行时间。
最坏情况 - 这是特定数据结构操作可能花费的最长时间的情况。如果操作的最坏情况时间为 ƒ(n),则此操作不会花费超过 ƒ(n) 时间,其中 ƒ(n) 表示 n 的函数。
平均情况 - 这表示数据结构操作的平均执行时间的情况。如果操作执行时间为 ƒ(n),则 m 个操作将花费 mƒ(n) 时间。
最佳情况 - 这表示数据结构操作可能的最小执行时间的情况。如果操作执行时间为 ƒ(n),则实际操作可能花费的时间为随机数,其最大值为 ƒ(n)。
Java 数据结构与算法 - 环境搭建
本地环境搭建
如果您仍然希望为 Java 编程语言设置环境,那么本节将指导您如何在计算机上下载和设置 Java。请按照以下步骤设置环境。
Java SE 可从以下链接免费获得 下载 Java。因此,您可以根据您的操作系统下载一个版本。
按照说明下载 java 并运行 .exe 文件以在您的计算机上安装 Java。在您的计算机上安装 Java 后,您需要设置环境变量以指向正确的安装目录。
为 Windows 2000/XP 设置路径
假设您已将 Java 安装在 c:\Program Files\java\jdk 目录中
右键单击“我的电脑”,然后选择“属性”。
在“高级”选项卡下单击“环境变量”按钮。
现在更改“Path”变量,使其还包含 Java 可执行文件的路径。例如,如果路径当前设置为“C:\WINDOWS\SYSTEM32”,则将路径更改为“C:\WINDOWS\SYSTEM32;c:\Program Files\java\jdk\bin”。
为 Windows 95/98/ME 设置路径
假设您已将 Java 安装在 c:\Program Files\java\jdk 目录中 -
编辑“C:\autoexec.bat”文件,并在末尾添加以下行
“SET PATH=%PATH%;C:\Program Files\java\jdk\bin”
为 Linux、UNIX、Solaris、FreeBSD 设置路径
环境变量 PATH 应设置为指向已安装 java 二进制文件的目录。如果您遇到问题,请参考您的 shell 文档。
例如,如果您使用 bash 作为您的 shell,则您将在您的“.bashrc”的末尾添加以下行:export PATH=/path/to/java:$PATH
常用的 Java 编辑器
要编写 Java 程序,您需要一个文本编辑器。市场上还有更复杂的 IDE。但就目前而言,您可以考虑以下其中一种
记事本 -在 Windows 机器上,您可以使用任何简单的文本编辑器,如记事本(本教程推荐)、TextPad。
Netbeans -是一个开源且免费的 Java IDE,可以从 https://www.netbeans.org/index.html 下载。
Eclipse -也是一个由 Eclipse 开源社区开发的 Java IDE,可以从 https://www.eclipse.org/ 下载。
接下来是什么?
下一章将教您如何编写和运行您的第一个 Java 程序以及开发应用程序所需的一些重要的基本 Java 语法。
Java 数据结构与算法 - 算法
算法概念
算法是一个逐步的过程,它定义了一组指令,这些指令以一定的顺序执行以获得所需的输出。就数据结构而言,算法的类别如下。
搜索 - 用于在数据结构中搜索项目的算法。
排序 - 用于按特定顺序排序项目的算法
插入 - 用于将项目插入数据结构的算法
更新 - 用于更新数据结构中现有项目的算法
删除 - 用于从数据结构中删除现有项目的算法
算法分析
算法分析处理数据结构的各种操作的执行时间或运行时间。操作的运行时间可以定义为每个操作执行的计算机指令数。由于任何操作的确切运行时间因计算机而异,我们通常将任何操作的运行时间分析为 n 的某个函数,其中 n 是数据结构中该操作处理的项目数。
渐近分析
渐近分析是指使用数学计算单位计算任何操作的运行时间。例如,一个操作的运行时间计算为 *f*(n),另一个操作的运行时间计算为 *g*(n2)。这意味着第一个操作的运行时间将随着 n 的增加而线性增加,而第二个操作的运行时间将随着 n 的增加而呈指数增加。同样,如果 n 足够小,则两个操作的运行时间几乎相同。
渐近符号
以下是计算算法运行时间复杂度时常用的渐近符号。
Ο 符号
Ω 符号
θ 符号
大 O 符号,Ο
Ο(n) 是表达算法运行时间上限的形式化方法。它衡量最坏情况下的时间复杂度或算法可能完成所需的最长时间。例如,对于函数 *f*(n)大 O 符号用于简化函数。例如,我们可以用 Ο(*f*(nlogn)) 代替特定的函数方程 7nlogn + n - 1。考虑以下情况
它表明 *f*(n) = 7nlogn + n - 1 位于使用常数 c = 8 和 n0 = 2 的 *O*(nlogn) 输出范围内。
Omega 符号,Ω
Ω(n) 是表达算法运行时间下限的形式化方法。它衡量最佳情况下的时间复杂度或算法可能完成所需的最短时间。
例如,对于函数 *f*(n)
Theta 符号,θ
θ(n) 是表达算法运行时间下限和上限的形式化方法。它表示如下。
Java 数据结构与算法 - 数据结构
数据结构是以一种有效的方式组织数据的方法。以下术语是数据结构的基本术语。
数据定义
数据定义定义了具有以下特征的特定数据。
原子性 - 定义应定义单个概念
可跟踪性 - 定义应该能够映射到某些数据元素。
准确性 - 定义应明确无误。
清晰简洁 - 定义应该易于理解。
数据对象
数据对象表示具有数据的对象。
数据类型
数据类型是分类各种类型的数据(例如整数、字符串等)的方法,它决定了可以与相应类型的数据一起使用的值以及可以对相应类型的数据执行的操作。数据类型分为两种 -
内置数据类型
派生数据类型
内置数据类型
语言对那些具有内置支持的数据类型称为内置数据类型。例如,大多数语言提供以下内置数据类型。
整数
布尔值 (true, false)
浮点数 (十进制数)
字符和字符串
派生数据类型
那些数据类型因为可以以一种或另一种方式实现而与实现无关,被称为派生数据类型。这些数据类型通常由组合的基本数据类型或内置数据类型以及对它们的关联操作构建而成。例如:
列表
数组
栈
队列
Java中的数据结构 - 数组
数组基础
数组是一个容器,可以容纳固定数量的项,并且这些项的类型必须相同。大多数数据结构都利用数组来实现其算法。以下是理解数组概念的重要术语:
元素 - 存储在数组中的每一项都称为元素。
索引 - 数组中每个元素的位置都有一个数值索引,用于标识该元素。
数组表示
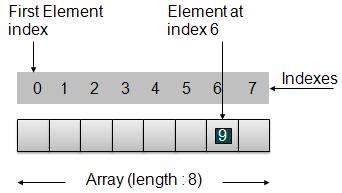
根据上图所示,需要考虑以下要点:
索引从0开始。
数组长度为8,这意味着它可以存储8个元素。
每个元素都可以通过其索引访问。例如,我们可以获取索引为6的元素,值为9。
基本操作
以下是数组支持的基本操作:
插入 - 在给定索引处添加元素。
删除 - 删除给定索引处的元素。
搜索 - 使用给定索引或值搜索元素。
更新 - 更新给定索引处的元素。
在Java中,当数组初始化为特定大小时,它会按照以下顺序为其元素分配默认值:
| 数据类型 | 默认值 |
|---|---|
| byte | 0 |
| short | 0 |
| int | 0 |
| long | 0L |
| float | 0.0f |
| double | 0.0d |
| char | '\u0000' |
| boolean | false |
| Object | null |
演示
package com.tutorialspoint.array;
public class ArrayDemo {
public static void main(String[] args){
// Declare an array
int intArray[];
// Initialize an array of 8 int
// set aside memory of 8 int
intArray = new int[8];
System.out.println("Array before adding data.");
// Display elements of an array.
display(intArray);
// Operation : Insertion
// Add elements in the array
for(int i = 0; i< intArray.length; i++)
{
// place value of i at index i.
System.out.println("Adding "+i+" at index "+i);
intArray[i] = i;
}
System.out.println();
System.out.println("Array after adding data.");
display(intArray);
// Operation : Insertion
// Element at any location can be updated directly
int index = 5;
intArray[index] = 10;
System.out.println("Array after updating element at index " + index);
display(intArray);
// Operation : Search using index
// Search an element using index.
System.out.println("Data at index " + index + ": "+ intArray[index]);
// Operation : Search using value
// Search an element using value.
int value = 4;
for(int i = 0; i< intArray.length; i++)
{
if(intArray[i] == value ){
System.out.println(value + " Found at index "+i);
break;
}
}
System.out.println("Data at index " + index + ": "+ intArray[index]);
}
private static void display(int[] intArray){
System.out.print("Array : [");
for(int i = 0; i< intArray.length; i++)
{
// display value of element at index i.
System.out.print(" "+intArray[i]);
}
System.out.println(" ]");
System.out.println();
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Array before adding data. Array : [ 0 0 0 0 0 0 0 0 ] Adding 0 at index 0 Adding 1 at index 1 Adding 2 at index 2 Adding 3 at index 3 Adding 4 at index 4 Adding 5 at index 5 Adding 6 at index 6 Adding 7 at index 7 Array after adding data. Array : [ 0 1 2 3 4 5 6 7 ] Array after updating element at index 5 Array : [ 0 1 2 3 4 10 6 7 ] Data at index 5: 10 4 Found at index: 4
Java 数据结构与算法 - 链表
链表基础
链表是由包含项的链接组成的序列。每个链接都包含到另一个链接的连接。链表是继数组之后第二常用的数据结构。以下是理解链表概念的重要术语:
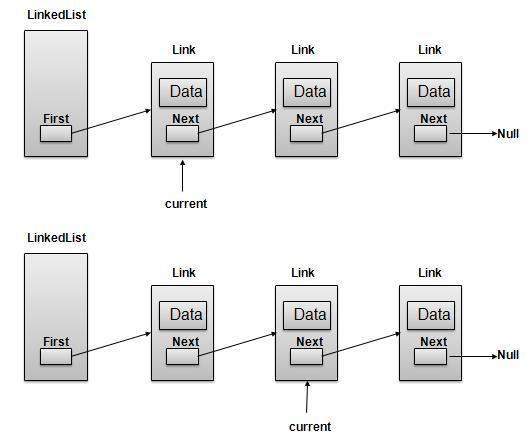
链接 - 链表的每个链接都可以存储称为元素的数据。
下一个 - 链表的每个链接都包含指向下一个链接的链接,称为“下一个”。
链表 - 链表包含指向第一个链接的连接链接,称为“第一个”。
链表表示
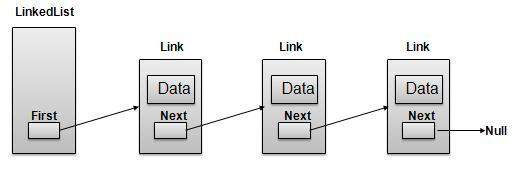
根据上图所示,需要考虑以下要点:
链表包含一个称为first的链接元素。
每个链接都包含一个或多个数据字段和一个称为next的链接字段。
每个链接都使用其next链接与其下一个链接链接。
最后一个链接包含一个值为null的链接,以标记列表的结尾。
链表的类型
以下是链表的各种类型:
单链表 - 项目导航仅向前。
双向链表 - 项目可以向前和向后导航。
循环链表 - 最后一项包含下一个元素的第一个元素的链接,第一个元素包含上一个元素的最后一个元素的链接。
基本操作
以下是列表支持的基本操作:
插入 - 在列表开头添加元素。
删除 - 删除列表开头的元素。
显示 - 显示完整列表。
搜索 - 使用给定键搜索元素。
删除 - 使用给定键删除元素。
插入操作
插入是一个三步过程:
创建一个包含提供的数据的新链接。
将新链接指向旧的第一个链接。
将第一个链接指向此新链接。
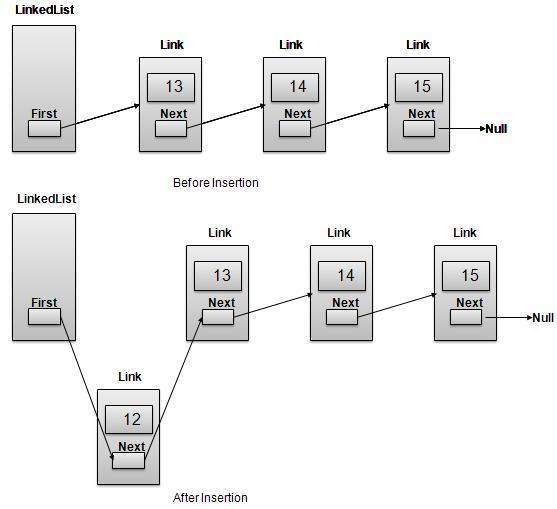
//insert link at the first location
public void insertFirst(int key, int data){
//create a link
Link link = new Link(key,data);
//point it to old first node
link.next = first;
//point first to new first node
first = link;
}
删除操作
删除是一个两步过程:
获取第一个链接指向的链接作为临时链接。
将第一个链接指向临时链接的下一个链接。
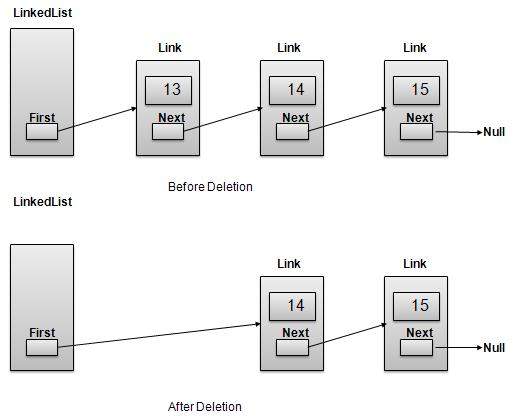
//delete first item
public Link deleteFirst(){
//save reference to first link
Link tempLink = first;
//mark next to first link as first
first = first.next;
//return the deleted link
return tempLink;
}
导航操作
导航是一个递归步骤过程,是许多操作(如搜索、删除等)的基础。
获取第一个链接指向的链接作为当前链接。
检查当前链接是否不为null并显示它。
将当前链接指向当前链接的下一个链接并移动到上述步骤。
注意
//display the list
public void display(){
//start from the beginning
Link current = first;
//navigate till the end of the list
System.out.print("[ ");
while(current != null){
//print data
current.display();
//move to next item
current = current.next;
System.out.print(" ");
}
System.out.print(" ]");
}
高级操作
以下是为列表指定的高级操作:
排序 - 基于特定顺序对列表进行排序。
反转 - 反转链表。
连接 - 连接两个列表。
排序操作
我们使用冒泡排序来排序列表。
public void sort(){
int i, j, k, tempKey, tempData ;
Link current,next;
int size = length();
k = size ;
for ( i = 0 ; i < size - 1 ; i++, k-- ) {
current = first ;
next = first.next ;
for ( j = 1 ; j < k ; j++ ) {
if ( current.data > next.data ) {
tempData = current.data ;
current.data = next.data;
next.data = tempData ;
tempKey = current.key;
current.key = next.key;
next.key = tempKey;
}
current = current.next;
next = next.next;
}
}
}
反转操作
以下代码演示了反转单链表。
public LinkedList reverse() {
LinkedList reversedlist = new LinkedList();
Link nextLink = null;
reversedlist.insertFirst(first.key, first.data);
Link currentLink = first;
// Until no more data in list,
// insert current link before first and move ahead.
while(currentLink.next != null){
nextLink = currentLink.next;
// Insert at start of new list.
reversedlist.insertFirst(nextLink.key, nextLink.data);
//advance to next node
currentLink = currentLink.next;
}
return reversedlist;
}
连接操作
以下代码演示了反转单链表。
public void concatenate(LinkedList list){
if(first == null){
first = list.first;
}
if(list.first == null){
return;
}
Link temp = first;
while(temp.next !=null) {
temp = temp.next;
}
temp.next = list.first;
}
演示
Link.javapackage com.tutorialspoint.list;
public class Link {
public int key;
public int data;
public Link next;
public Link(int key, int data){
this.key = key;
this.data = data;
}
public void display(){
System.out.print("{"+key+","+data+"}");
}
}
LinkedList.java
package com.tutorialspoint.list;
public class LinkedList {
//this link always point to first Link
//in the Linked List
private Link first;
// create an empty linked list
public LinkedList(){
first = null;
}
//insert link at the first location
public void insertFirst(int key, int data){
//create a link
Link link = new Link(key,data);
//point it to old first node
link.next = first;
//point first to new first node
first = link;
}
//delete first item
public Link deleteFirst(){
//save reference to first link
Link tempLink = first;
//mark next to first link as first
first = first.next;
//return the deleted link
return tempLink;
}
//display the list
public void display(){
//start from the beginning
Link current = first;
//navigate till the end of the list
System.out.print("[ ");
while(current != null){
//print data
current.display();
//move to next item
current = current.next;
System.out.print(" ");
}
System.out.print(" ]");
}
//find a link with given key
public Link find(int key){
//start from the first link
Link current = first;
//if list is empty
if(first == null){
return null;
}
//navigate through list
while(current.key != key){
//if it is last node
if(current.next == null){
return null;
}else{
//go to next link
current = current.next;
}
}
//if data found, return the current Link
return current;
}
//delete a link with given key
public Link delete(int key){
//start from the first link
Link current = first;
Link previous = null;
//if list is empty
if(first == null){
return null;
}
//navigate through list
while(current.key != key){
//if it is last node
if(current.next == null){
return null;
}else{
//store reference to current link
previous = current;
//move to next link
current = current.next;
}
}
//found a match, update the link
if(current == first) {
//change first to point to next link
first = first.next;
}else {
//bypass the current link
previous.next = current.next;
}
return current;
}
//is list empty
public boolean isEmpty(){
return first == null;
}
public int length(){
int length = 0;
for(Link current = first; current!=null;
current = current.next){
length++;
}
return length;
}
public void sort(){
int i, j, k, tempKey, tempData ;
Link current,next;
int size = length();
k = size ;
for ( i = 0 ; i < size - 1 ; i++, k-- ) {
current = first ;
next = first.next ;
for ( j = 1 ; j < k ; j++ ) {
if ( current.data > next.data ) {
tempData = current.data ;
current.data = next.data;
next.data = tempData ;
tempKey = current.key;
current.key = next.key;
next.key = tempKey;
}
current = current.next;
next = next.next;
}
}
}
public LinkedList reverse() {
LinkedList reversedlist = new LinkedList();
Link nextLink = null;
reversedlist.insertFirst(first.key, first.data);
Link currentLink = first;
// Until no more data in list,
// insert current link before first and move ahead.
while(currentLink.next != null){
nextLink = currentLink.next;
// Insert at start of new list.
reversedlist.insertFirst(nextLink.key, nextLink.data);
//advance to next node
currentLink = currentLink.next;
}
return reversedlist;
}
public void concatenate(LinkedList list){
if(first == null){
first = list.first;
}
if(list.first == null){
return;
}
Link temp = first;
while(temp.next !=null) {
temp = temp.next;
}
temp.next = list.first;
}
}
LinkedListDemo.java
package com.tutorialspoint.list;
public class LinkedListDemo {
public static void main(String args[]){
LinkedList list = new LinkedList();
list.insertFirst(1, 10);
list.insertFirst(2, 20);
list.insertFirst(3, 30);
list.insertFirst(4, 1);
list.insertFirst(5, 40);
list.insertFirst(6, 56);
System.out.print("\nOriginal List: ");
list.display();
System.out.println("");
while(!list.isEmpty()){
Link temp = list.deleteFirst();
System.out.print("Deleted value:");
temp.display();
System.out.println("");
}
System.out.print("List after deleting all items: ");
list.display();
System.out.println("");
list.insertFirst(1, 10);
list.insertFirst(2, 20);
list.insertFirst(3, 30);
list.insertFirst(4, 1);
list.insertFirst(5, 40);
list.insertFirst(6, 56);
System.out.print("Restored List: ");
list.display();
System.out.println("");
Link foundLink = list.find(4);
if(foundLink != null){
System.out.print("Element found: ");
foundLink.display();
System.out.println("");
}else{
System.out.println("Element not found.");
}
list.delete(4);
System.out.print("List after deleting an item: ");
list.display();
System.out.println("");
foundLink = list.find(4);
if(foundLink != null){
System.out.print("Element found: ");
foundLink.display();
System.out.println("");
}else{
System.out.print("Element not found. {4,1}");
}
System.out.println("");
list.sort();
System.out.print("List after sorting the data: ");
list.display();
System.out.println("");
System.out.print("Reverse of the list: ");
LinkedList list1 = list.reverse();
list1.display();
System.out.println("");
LinkedList list2 = new LinkedList();
list2.insertFirst(9, 50);
list2.insertFirst(8, 40);
list2.insertFirst(7, 20);
list.concatenate(list2);
System.out.print("List after concatenation: ");
list.display();
System.out.println("");
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Original List: [ {6,56} {5,40} {4,1} {3,30} {2,20} {1,10} ]
Deleted value:{6,56}
Deleted value:{5,40}
Deleted value:{4,1}
Deleted value:{3,30}
Deleted value:{2,20}
Deleted value:{1,10}
List after deleting all items: [ ]
Restored List: [ {6,56} {5,40} {4,1} {3,30} {2,20} {1,10} ]
Element found: {4,1}
List after deleting an item: [ {6,56} {5,40} {3,30} {2,20} {1,10} ]
Element not found. {4,1}
List after sorting the data: [ {1,10} {2,20} {3,30} {5,40} {6,56} ]
Reverse of the list: [ {6,56} {5,40} {3,30} {2,20} {1,10} ]
List after concatenation: [ {1,10} {2,20} {3,30} {5,40} {6,56} {7,20} {8,40} {9,50} ]
Java 数据结构与算法 - 双向链表
双向链表基础
双向链表是链表的一种变体,与单链表相比,它可以轻松地向前和向后两种方式进行导航。以下是理解双向链表概念的重要术语:
链接 - 链表的每个链接都可以存储称为元素的数据。
下一个 - 链表的每个链接都包含指向下一个链接的链接,称为“下一个”。
前一个 - 链表的每个链接都包含指向前一个链接的链接,称为“前一个”。
链表 - 链表包含指向第一个链接的连接链接(称为“第一个”)和指向最后一个链接的链接(称为“最后一个”)。
双向链表表示
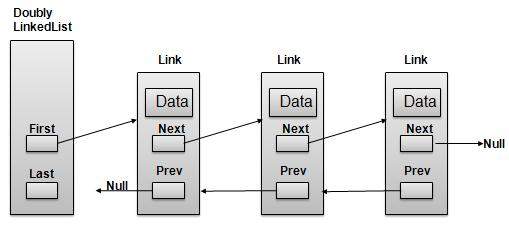
根据上图所示,需要考虑以下要点:
双向链表包含一个称为first和last的链接元素。
每个链接都包含一个或多个数据字段和一个称为next的链接字段。
每个链接都使用其next链接与其下一个链接链接。
每个链接都使用其prev链接与其前一个链接链接。
最后一个链接包含一个值为null的链接,以标记列表的结尾。
基本操作
以下是列表支持的基本操作:
插入 - 在列表开头添加元素。
删除 - 删除列表开头的元素。
插入末尾 - 在列表末尾添加元素。
删除末尾 - 从列表末尾删除元素。
插入到之后 - 在列表项之后添加元素。
删除 - 使用键从列表中删除元素。
向前显示 - 以向前的方式显示完整列表。
向后显示 - 以向后的方式显示完整列表。
插入操作
以下代码演示了在双向链表开头进行插入操作。
//insert link at the first location
public void insertFirst(int key, int data){
//create a link
Link link = new Link(key,data);
if(isEmpty()){
//make it the last link
last = link;
}else {
//update first prev link
first.prev = link;
}
//point it to old first link
link.next = first;
//point first to new first link
first = link;
}
删除操作
以下代码演示了在双向链表开头进行删除操作。
//delete link at the first location
public Link deleteFirst(){
//save reference to first link
Link tempLink = first;
//if only one link
if(first.next == null){
last = null;
}else {
first.next.prev = null;
}
first = first.next;
//return the deleted link
return tempLink;
}
在末尾插入操作
以下代码演示了在双向链表的最后位置进行插入操作。
//insert link at the last location
public void insertLast(int key, int data){
//create a link
Link link = new Link(key,data);
if(isEmpty()){
//make it the last link
last = link;
}else {
//make link a new last link
last.next = link;
//mark old last node as prev of new link
link.prev = last;
}
//point last to new last node
last = link;
}
演示
Link.java
package com.tutorialspoint.list;
public class Link {
public int key;
public int data;
public Link next;
public Link prev;
public Link(int key, int data){
this.key = key;
this.data = data;
}
public void display(){
System.out.print("{"+key+","+data+"}");
}
}
DoublyLinkedList.java
package com.tutorialspoint.list;
public class DoublyLinkedList {
//this link always point to first Link
private Link first;
//this link always point to last Link
private Link last;
// create an empty linked list
public DoublyLinkedList(){
first = null;
last = null;
}
//is list empty
public boolean isEmpty(){
return first == null;
}
//insert link at the first location
public void insertFirst(int key, int data){
//create a link
Link link = new Link(key,data);
if(isEmpty()){
//make it the last link
last = link;
}else {
//update first prev link
first.prev = link;
}
//point it to old first link
link.next = first;
//point first to new first link
first = link;
}
//insert link at the last location
public void insertLast(int key, int data){
//create a link
Link link = new Link(key,data);
if(isEmpty()){
//make it the last link
last = link;
}else {
//make link a new last link
last.next = link;
//mark old last node as prev of new link
link.prev = last;
}
//point last to new last node
last = link;
}
//delete link at the first location
public Link deleteFirst(){
//save reference to first link
Link tempLink = first;
//if only one link
if(first.next == null){
last = null;
}else {
first.next.prev = null;
}
first = first.next;
//return the deleted link
return tempLink;
}
//delete link at the last location
public Link deleteLast(){
//save reference to last link
Link tempLink = last;
//if only one link
if(first.next == null){
first = null;
}else {
last.prev.next = null;
}
last = last.prev;
//return the deleted link
return tempLink;
}
//display the list in from first to last
public void displayForward(){
//start from the beginning
Link current = first;
//navigate till the end of the list
System.out.print("[ ");
while(current != null){
//print data
current.display();
//move to next item
current = current.next;
System.out.print(" ");
}
System.out.print(" ]");
}
//display the list from last to first
public void displayBackward(){
//start from the last
Link current = last;
//navigate till the start of the list
System.out.print("[ ");
while(current != null){
//print data
current.display();
//move to next item
current = current.prev;
System.out.print(" ");
}
System.out.print(" ]");
}
//delete a link with given key
public Link delete(int key){
//start from the first link
Link current = first;
//if list is empty
if(first == null){
return null;
}
//navigate through list
while(current.key != key){
//if it is last node
if(current.next == null){
return null;
}else{
//move to next link
current = current.next;
}
}
//found a match, update the link
if(current == first) {
//change first to point to next link
first = current.next;
}else {
//bypass the current link
current.prev.next = current.next;
}
if(current == last){
//change last to point to prev link
last = current.prev;
}else {
current.next.prev = current.prev;
}
return current;
}
public boolean insertAfter(int key, int newKey, int data){
//start from the first link
Link current = first;
//if list is empty
if(first == null){
return false;
}
//navigate through list
while(current.key != key){
//if it is last node
if(current.next == null){
return false;
}else{
//move to next link
current = current.next;
}
}
Link newLink = new Link(newKey,data);
if(current==last) {
newLink.next = null;
last = newLink;
}
else {
newLink.next = current.next;
current.next.prev = newLink;
}
newLink.prev = current;
current.next = newLink;
return true;
}
}
DoublyLinkedListDemo.java
package com.tutorialspoint.list;
public class DoublyLinkedListDemo {
public static void main(String args[]){
DoublyLinkedList list = new DoublyLinkedList();
list.insertFirst(1, 10);
list.insertFirst(2, 20);
list.insertFirst(3, 30);
list.insertLast(4, 1);
list.insertLast(5, 40);
list.insertLast(6, 56);
System.out.print("\nList (First to Last): ");
list.displayForward();
System.out.println("");
System.out.print("\nList (Last to first): ");
list.displayBackward();
System.out.print("\nList , after deleting first record: ");
list.deleteFirst();
list.displayForward();
System.out.print("\nList , after deleting last record: ");
list.deleteLast();
list.displayForward();
System.out.print("\nList , insert after key(4) : ");
list.insertAfter(4,7, 13);
list.displayForward();
System.out.print("\nList , after delete key(4) : ");
list.delete(4);
list.displayForward();
}
}
如果我们编译并运行上述程序,则会产生以下结果:
List (First to Last): [ {3,30} {2,20} {1,10} {4,1} {5,40} {6,56} ]
List (Last to first): [ {6,56} {5,40} {4,1} {1,10} {2,20} {3,30} ]
List (First to Last) after deleting first record: [ {2,20} {1,10} {4,1} {5,40} {6,56} ]
List (First to Last) after deleting last record: [ {2,20} {1,10} {4,1} {5,40} ]
List (First to Last) insert after key(4) : [ {2,20} {1,10} {4,1} {7,13} {5,40} ]
List (First to Last) after delete key(4) : [ {2,20} {1,10} {7,13} {5,40} ]
Java 数据结构与算法 - 循环链表
循环链表基础
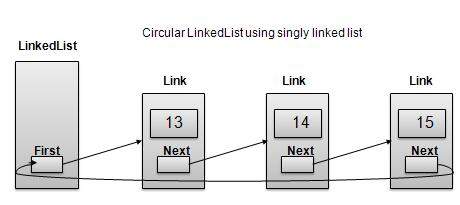
循环链表是链表的一种变体,其中第一个元素指向最后一个元素,最后一个元素指向第一个元素。单链表和双向链表都可以制成循环链表。
单链表作为循环链表
双向链表作为循环链表
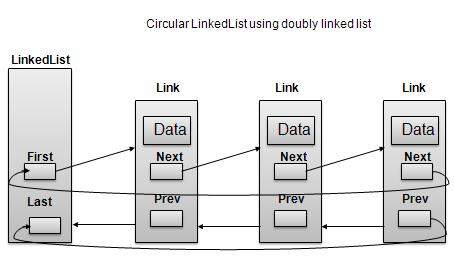
根据上图所示,需要考虑以下要点:
在单链表和双向链表这两种情况下,最后一个链接的next都指向列表的第一个链接。
在双向链表的情况下,第一个链接的prev指向列表的最后一个。
基本操作
以下是循环列表支持的重要操作:
插入 - 在列表开头插入元素。
删除 - 从列表开头删除元素。
显示 - 显示列表。
长度操作
以下代码演示了基于单链表的循环链表中的插入操作。
//insert link at the first location
public void insertFirst(int key, int data){
//create a link
Link link = new Link(key,data);
if (isEmpty()) {
first = link;
first.next = first;
}
else{
//point it to old first node
link.next = first;
//point first to new first node
first = link;
}
}
删除操作
以下代码演示了基于单链表的循环链表中的删除操作。
//delete link at the first location
public Link deleteFirst(){
//save reference to first link
Link tempLink = first;
//if only one link
if(first.next == null){
last = null;
}else {
first.next.prev = null;
}
first = first.next;
//return the deleted link
return tempLink;
}
显示列表操作
以下代码演示了循环链表中的显示列表操作。
public void display(){
//start from the beginning
Link current = first;
//navigate till the end of the list
System.out.print("[ ");
if(first != null){
while(current.next != current){
//print data
current.display();
//move to next item
current = current.next;
System.out.print(" ");
}
}
System.out.print(" ]");
}
演示
Link.java
package com.tutorialspoint.list;
public class CircularLinkedList {
//this link always point to first Link
private Link first;
// create an empty linked list
public CircularLinkedList(){
first = null;
}
public boolean isEmpty(){
return first == null;
}
public int length(){
int length = 0;
//if list is empty
if(first == null){
return 0;
}
Link current = first.next;
while(current != first){
length++;
current = current.next;
}
return length;
}
//insert link at the first location
public void insertFirst(int key, int data){
//create a link
Link link = new Link(key,data);
if (isEmpty()) {
first = link;
first.next = first;
}
else{
//point it to old first node
link.next = first;
//point first to new first node
first = link;
}
}
//delete first item
public Link deleteFirst(){
//save reference to first link
Link tempLink = first;
if(first.next == first){
first = null;
return tempLink;
}
//mark next to first link as first
first = first.next;
//return the deleted link
return tempLink;
}
public void display(){
//start from the beginning
Link current = first;
//navigate till the end of the list
System.out.print("[ ");
if(first != null){
while(current.next != current){
//print data
current.display();
//move to next item
current = current.next;
System.out.print(" ");
}
}
System.out.print(" ]");
}
}
DoublyLinkedListDemo.java
package com.tutorialspoint.list;
public class CircularLinkedListDemo {
public static void main(String args[]){
CircularLinkedList list = new CircularLinkedList();
list.insertFirst(1, 10);
list.insertFirst(2, 20);
list.insertFirst(3, 30);
list.insertFirst(4, 1);
list.insertFirst(5, 40);
list.insertFirst(6, 56);
System.out.print("\nOriginal List: ");
list.display();
System.out.println("");
while(!list.isEmpty()){
Link temp = list.deleteFirst();
System.out.print("Deleted value:");
temp.display();
System.out.println("");
}
System.out.print("List after deleting all items: ");
list.display();
System.out.println("");
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Original List: [ {6,56} {5,40} {4,1} {3,30} {2,20} ]
Deleted value:{6,56}
Deleted value:{5,40}
Deleted value:{4,1}
Deleted value:{3,30}
Deleted value:{2,20}
Deleted value:{1,10}
List after deleting all items: [ ]
Java 数据结构与算法 - 栈
概述
栈是一种数据结构,它只允许对一端的数据进行操作。它只允许访问最后插入的数据。栈也称为LIFO(后进先出)数据结构,push和pop操作以这样一种方式相关联:只有最后一个push(添加到栈中)的项才能pop(从栈中移除)。
栈表示
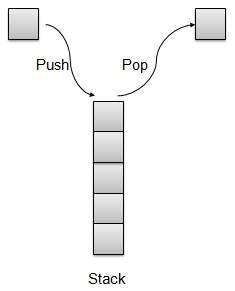
我们将在本文中使用数组来实现栈。
基本操作
以下是栈的两个主要操作:
push - 将元素压入栈顶。
pop - 从栈顶弹出元素。
栈还支持一些其他操作:
peek - 获取栈顶元素。
isFull - 检查栈是否已满。
isEmpty - 检查栈是否为空。
push操作
每当一个元素被压入栈时,栈将该元素存储在存储区的顶部,并增加顶部索引以备后用。如果存储区已满,则通常会显示错误消息。
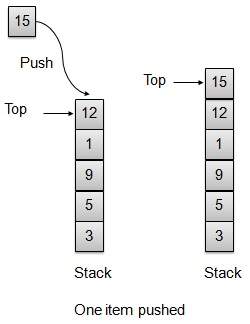
// push item on the top of the stack
public void push(int data) {
if(!isFull()){
// increment top by 1 and insert data
intArray[++top] = data;
}else{
System.out.println("Cannot add data. Stack is full.");
}
}
pop操作
每当要从栈中弹出元素时,栈会从存储区的顶部检索元素,并减少顶部索引以备后用。
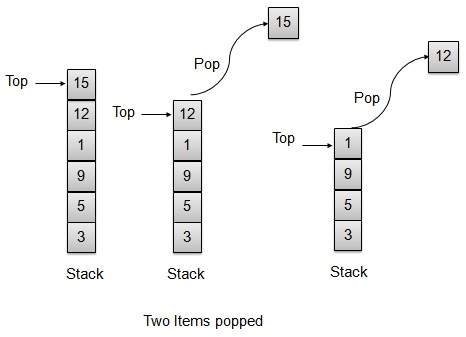
// pop item from the top of the stack
public int pop() {
// retrieve data and decrement the top by 1
return intArray[top--];
}
栈实现
Stack.java
package com.tutorialspoint.datastructure;
public class Stack {
private int size; // size of the stack
private int[] intArray; // stack storage
private int top; // top of the stack
// Constructor
public Stack(int size){
this.size = size;
intArray = new int[size]; //initialize array
top = -1; //stack is initially empty
}
// Operation : Push
// push item on the top of the stack
public void push(int data) {
if(!isFull()){
// increment top by 1 and insert data
intArray[++top] = data;
}else{
System.out.println("Cannot add data. Stack is full.");
}
}
// Operation : Pop
// pop item from the top of the stack
public int pop() {
//retrieve data and decrement the top by 1
return intArray[top--];
}
// Operation : Peek
// view the data at top of the stack
public int peek() {
//retrieve data from the top
return intArray[top];
}
// Operation : isFull
// return true if stack is full
public boolean isFull(){
return (top == size-1);
}
// Operation : isEmpty
// return true if stack is empty
public boolean isEmpty(){
return (top == -1);
}
}
演示程序
StackDemo.java
package com.tutorialspoint.datastructure;
public class StackDemo {
public static void main (String[] args){
// make a new stack
Stack stack = new Stack(10);
// push items on to the stack
stack.push(3);
stack.push(5);
stack.push(9);
stack.push(1);
stack.push(12);
stack.push(15);
System.out.println("Element at top of the stack: " + stack.peek());
System.out.println("Elements: ");
// print stack data
while(!stack.isEmpty()){
int data = stack.pop();
System.out.println(data);
}
System.out.println("Stack full: " + stack.isFull());
System.out.println("Stack empty: " + stack.isEmpty());
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Element at top of the stack: 15 Elements: 15 12 1 9 5 3 Stack full: false Stack empty: true
Java中的数据结构 - 解析表达式
像2*(3*4)这样的普通算术表达式对于人类大脑来说更容易解析,但是对于算法来说,解析这样的表达式相当困难。为了减轻这种困难,可以使用两步法通过算法解析算术表达式。
将提供的算术表达式转换为后缀表示法。
评估后缀表示法。
中缀表示法
普通的算术表达式遵循中缀表示法,其中运算符位于操作数之间。例如,A+B,其中A是第一个操作数,B是第二个操作数,+是作用于这两个操作数的运算符。
后缀表示法
后缀表示法与普通的算术表达式或中缀表示法的不同之处在于运算符位于操作数之后。例如,考虑以下示例:
| 序号 | 中缀表示法 | 后缀表示法 |
|---|---|---|
| 1 | A+B | AB+ |
| 2 | (A+B)*C | AB+C* |
| 3 | A*(B+C) | ABC+* |
| 4 | A/B+C/D | AB/CD/+ |
| 5 | (A+B)*(C+D) | AB+CD+* |
| 6 | ((A+B)*C)-D | AB+C*D- |
中缀转后缀转换
在研究将中缀转换为后缀表示法的方法之前,我们需要考虑中缀表达式求值的以下基础知识。
中缀表达式的求值从左到右开始。
记住优先级,例如*的优先级高于+。例如:
2+3*4 = 2+12.
2+3*4 = 14.
使用括号覆盖优先级,例如:
(2+3)*4 = 5*4.
(2+3)*4= 20.
现在让我们手动将简单的中缀表达式A+B*C转换为后缀表达式。
| 步骤 | 读取的字符 | 到目前为止已解析的中缀表达式 | 到目前为止已生成的后续表达式 | 备注 |
|---|---|---|---|---|
| 1 | A | A | A | |
| 2 | + | A+ | A | |
| 3 | B | A+B | AB | |
| 4 | * | A+B* | AB | 不能复制+,因为*的优先级更高。 |
| 5 | C | A+B*C | ABC | |
| 6 | A+B*C | ABC* | 复制*,因为有两个操作数B和C | |
| 7 | A+B*C | ABC*+ | 复制+,因为有两个操作数BC和A |
现在让我们使用栈将上述中缀表达式A+B*C转换为后缀表达式。
| 步骤 | 读取的字符 | 到目前为止已解析的中缀表达式 | 到目前为止已生成的后续表达式 | 栈内容 | 备注 |
|---|---|---|---|---|---|
| 1 | A | A | A | ||
| 2 | + | A+ | A | + | 将+运算符压入栈中。 |
| 3 | B | A+B | AB | + | |
| 4 | * | A+B* | AB | +* | *运算符的优先级高于+。将*运算符压入栈中。否则,+将弹出。 |
| 5 | C | A+B*C | ABC | +* | |
| 6 | A+B*C | ABC* | + | 没有更多操作数,弹出*运算符。 | |
| 7 | A+B*C | ABC*+ | 弹出+运算符。 |
现在让我们看另一个例子,使用栈将中缀表达式A*(B+C)转换为后缀表达式。
| 步骤 | 读取的字符 | 到目前为止已解析的中缀表达式 | 到目前为止已生成的后续表达式 | 栈内容 | 备注 |
|---|---|---|---|---|---|
| 1 | A | A | A | ||
| 2 | * | A* | A | * | 将*运算符压入栈中。 |
| 3 | ( | A*( | A | *( | 将(压入栈中。 |
| 4 | B | A*(B | AB | *( | |
| 5 | + | A*(B+ | AB | *(+ | 将+压入栈中。 |
| 6 | C | A*(B+C | ABC | *(+ | |
| 7 | ) | A*(B+C) | ABC+ | *( | 弹出+运算符。 |
| 8 | A*(B+C) | ABC+ | * | 弹出(运算符。 | |
| 9 | A*(B+C) | ABC+* | 弹出其余的运算符。 |
演示程序
现在我们将演示如何使用栈将中缀表达式转换为后缀表达式,然后计算后缀表达式的值。
Stack.javapackage com.tutorialspoint.expression;
public class Stack {
private int size;
private int[] intArray;
private int top;
//Constructor
public Stack(int size){
this.size = size;
intArray = new int[size];
top = -1;
}
//push item on the top of the stack
public void push(int data) {
if(!isFull()){
//increment top by 1 and insert data
intArray[++top] = data;
}else{
System.out.println("Cannot add data. Stack is full.");
}
}
//pop item from the top of the stack
public int pop() {
//retrieve data and decrement the top by 1
return intArray[top--];
}
//view the data at top of the stack
public int peek() {
//retrieve data from the top
return intArray[top];
}
//return true if stack is full
public boolean isFull(){
return (top == size-1);
}
//return true if stack is empty
public boolean isEmpty(){
return (top == -1);
}
}
InfixToPostFix.java
package com.tutorialspoint.expression;
public class InfixToPostfix {
private Stack stack;
private String input = "";
private String output = "";
public InfixToPostfix(String input){
this.input = input;
stack = new Stack(input.length());
}
public String translate(){
for(int i=0;i<input.length();i++){
char ch = input.charAt(i);
switch(ch){
case '+':
case '-':
gotOperator(ch, 1);
break;
case '*':
case '/':
gotOperator(ch, 2);
break;
case '(':
stack.push(ch);
break;
case ')':
gotParenthesis(ch);
break;
default:
output = output+ch;
break;
}
}
while(!stack.isEmpty()){
output = output + (char)stack.pop();
}
return output;
}
//got operator from input
public void gotOperator(char operator, int precedence){
while(!stack.isEmpty()){
char prevOperator = (char)stack.pop();
if(prevOperator == '('){
stack.push(prevOperator);
break;
}else{
int precedence1;
if(prevOperator == '+' || prevOperator == '-'){
precedence1 = 1;
}else{
precedence1 = 2;
}
if(precedence1 < precedence){
stack.push(Character.getNumericValue(prevOperator));
break;
}else{
output = output + prevOperator;
}
}
}
stack.push(operator);
}
//got operator from input
public void gotParenthesis(char parenthesis){
while(!stack.isEmpty()){
char ch = (char)stack.pop();
if(ch == '('){
break;
}else{
output = output + ch;
}
}
}
}
PostFixParser.java
package com.tutorialspoint.expression;
public class PostFixParser {
private Stack stack;
private String input;
public PostFixParser(String postfixExpression){
input = postfixExpression;
stack = new Stack(input.length());
}
public int evaluate(){
char ch;
int firstOperand;
int secondOperand;
int tempResult;
for(int i=0;i<input.length();i++){
ch = input.charAt(i);
if(ch >= '0' && ch <= '9'){
stack.push(Character.getNumericValue(ch));
}else{
firstOperand = stack.pop();
secondOperand = stack.pop();
switch(ch){
case '+':
tempResult = firstOperand + secondOperand;
break;
case '-':
tempResult = firstOperand - secondOperand;
break;
case '*':
tempResult = firstOperand * secondOperand;
break;
case '/':
tempResult = firstOperand / secondOperand;
break;
default:
tempResult = 0;
}
stack.push(tempResult);
}
}
return stack.pop();
}
}
PostFixDemo.java
package com.tutorialspoint.expression;
public class PostFixDemo {
public static void main(String args[]){
String input = "1*(2+3)";
InfixToPostfix translator = new InfixToPostfix(input);
String output = translator.translate();
System.out.println("Infix expression is: " + input);
System.out.println("Postfix expression is: " + output);
PostFixParser parser = new PostFixParser(output);
System.out.println("Result is: " + parser.evaluate());
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Infix expression is: 1*(2+3) Postfix expression is: 123+* Result is: 5
Java 数据结构与算法 - 队列
概述
队列是一种类似于栈的数据结构,主要区别在于队列中第一个插入的元素也是第一个被移除的元素(FIFO - 先进先出),而栈则是基于LIFO(后进先出)原则。
队列表示
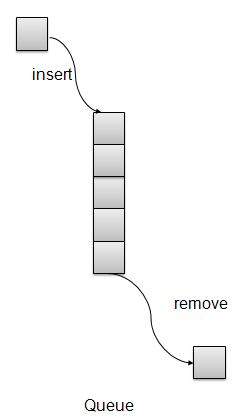
基本操作
插入/入队 − 将一个元素添加到队列的尾部。
移除/出队 − 从队列的头部移除一个元素。
在本文中,我们将使用数组来实现队列。队列还支持一些其他的操作:
Peek − 获取队列头部元素。
isFull − 检查队列是否已满。
isEmpty − 检查队列是否为空。
插入/入队操作
每当一个元素插入到队列中时,队列会递增尾部索引以备后用,并将该元素存储在存储空间的尾部。如果尾部到达最后一个索引,则会环绕到最底部位置。这种安排称为环绕,这种队列称为循环队列。此方法也称为入队操作。
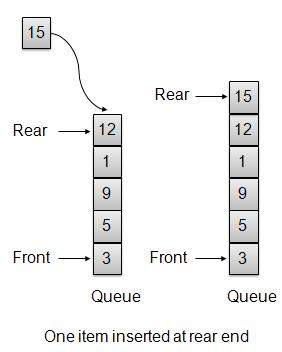
public void insert(int data){
if(!isFull()){
if(rear == MAX-1){
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
移除/出队操作
每当需要从队列中移除一个元素时,队列会使用头部索引获取该元素,然后递增头部索引。作为环绕安排的一部分,如果头部索引大于数组的最大索引,则将其设置为0。
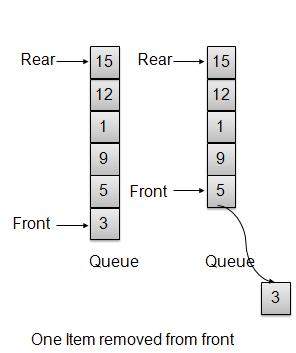
public int remove(){
int data = intArray[front++];
if(front == MAX){
front = 0;
}
itemCount--;
return data;
}
队列实现
Queue.java
package com.tutorialspoint.datastructure;
public class Queue {
private final int MAX;
private int[] intArray;
private int front;
private int rear;
private int itemCount;
public Queue(int size){
MAX = size;
intArray = new int[MAX];
front = 0;
rear = -1;
itemCount = 0;
}
public void insert(int data){
if(!isFull()){
if(rear == MAX-1){
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
public int remove(){
int data = intArray[front++];
if(front == MAX){
front = 0;
}
itemCount--;
return data;
}
public int peek(){
return intArray[front];
}
public boolean isEmpty(){
return itemCount == 0;
}
public boolean isFull(){
return itemCount == MAX;
}
public int size(){
return itemCount;
}
}
演示程序
QueueDemo.java
package com.tutorialspoint.datastructure;
public class QueueDemo {
public static void main(String[] args){
Queue queue = new Queue(6);
//insert 5 items
queue.insert(3);
queue.insert(5);
queue.insert(9);
queue.insert(1);
queue.insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
queue.insert(15);
// front : 0
// rear : 5
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 3 5 9 1 12 15
if(queue.isFull()){
System.out.println("Queue is full!");
}
//remove one item
int num = queue.remove();
System.out.println("Element removed: "+num);
// front : 1
// rear : 5
// -------------------
// index : 1 2 3 4 5
// -------------------
// queue : 5 9 1 12 15
//insert more items
queue.insert(16);
// front : 1
// rear : -1
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
//As queue is full, elements will not be inserted.
queue.insert(17);
queue.insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
System.out.println("Element at front: "+queue.peek());
System.out.println("----------------------");
System.out.println("index : 5 4 3 2 1 0");
System.out.println("----------------------");
System.out.print("Queue: ");
while(!queue.isEmpty()){
int n = queue.remove();
System.out.print(n +" ");
}
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
Java 数据结构与算法 - 优先队列
概述
优先队列比普通队列更专业的数据结构。与普通队列一样,优先队列具有相同的方法,但有一个主要区别。在优先队列中,项按键值排序,以便键值最低的项位于前端,键值最高的项位于后端,反之亦然。因此,我们根据项目的键值分配优先级。值越低,优先级越高。以下是优先队列的主要方法。
基本操作
插入/入队 − 将一个元素添加到队列的尾部。
移除/出队 − 从队列的头部移除一个元素。
优先队列表示

在本文中,我们将使用数组来实现队列。队列还支持一些其他的操作:
Peek − 获取队列头部元素。
isFull − 检查队列是否已满。
isEmpty − 检查队列是否为空。
插入/入队操作
每当一个元素插入到队列中时,优先队列会根据其顺序插入该元素。这里我们假设数据值越高,优先级越低。

public void insert(int data){
int i =0;
if(!isFull()){
// if queue is empty, insert the data
if(itemCount == 0){
intArray[itemCount++] = data;
}else{
// start from the right end of the queue
for(i = itemCount - 1; i >= 0; i-- ){
// if data is larger, shift existing item to right end
if(data > intArray[i]){
intArray[i+1] = intArray[i];
}else{
break;
}
}
// insert the data
intArray[i+1] = data;
itemCount++;
}
}
}
移除/出队操作
每当需要从队列中移除一个元素时,队列会使用项目计数获取该元素。移除元素后,项目计数减一。

public int remove(){
return intArray[--itemCount];
}
优先队列实现
PriorityQueue.java
package com.tutorialspoint.datastructure;
public class PriorityQueue {
private final int MAX;
private int[] intArray;
private int itemCount;
public PriorityQueue(int size){
MAX = size;
intArray = new int[MAX];
itemCount = 0;
}
public void insert(int data){
int i =0;
if(!isFull()){
// if queue is empty, insert the data
if(itemCount == 0){
intArray[itemCount++] = data;
}else{
// start from the right end of the queue
for(i = itemCount - 1; i >= 0; i-- ){
// if data is larger, shift existing item to right end
if(data > intArray[i]){
intArray[i+1] = intArray[i];
}else{
break;
}
}
// insert the data
intArray[i+1] = data;
itemCount++;
}
}
}
public int remove(){
return intArray[--itemCount];
}
public int peek(){
return intArray[itemCount - 1];
}
public boolean isEmpty(){
return itemCount == 0;
}
public boolean isFull(){
return itemCount == MAX;
}
public int size(){
return itemCount;
}
}
演示程序
PriorityQueueDemo.java
package com.tutorialspoint.datastructure;
public class PriorityQueueDemo {
public static void main(String[] args){
PriorityQueue queue = new PriorityQueue(6);
//insert 5 items
queue.insert(3);
queue.insert(5);
queue.insert(9);
queue.insert(1);
queue.insert(12);
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 12 9 5 3 1
queue.insert(15);
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 15 12 9 5 3 1
if(queue.isFull()){
System.out.println("Queue is full!");
}
//remove one item
int num = queue.remove();
System.out.println("Element removed: "+num);
// ---------------------
// index : 0 1 2 3 4
// ---------------------
// queue : 15 12 9 5 3
//insert more items
queue.insert(16);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 15 12 9 5 3
//As queue is full, elements will not be inserted.
queue.insert(17);
queue.insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 15 12 9 5 3
System.out.println("Element at front: "+queue.peek());
System.out.println("----------------------");
System.out.println("index : 5 4 3 2 1 0");
System.out.println("----------------------");
System.out.print("Queue: ");
while(!queue.isEmpty()){
int n = queue.remove();
System.out.print(n +" ");
}
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Queue is full! Element removed: 1 Element at front: 3 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 3 5 9 12 15 16
Java 数据结构与算法 - 树
概述
树表示由边连接的节点。我们将专门讨论二叉树或二叉搜索树。
二叉树是一种用于数据存储的特殊数据结构。二叉树有一个特殊条件,即每个节点最多可以有两个子节点。二叉树结合了有序数组和链表的优点,搜索速度与排序数组一样快,插入或删除操作与链表一样快。
术语
以下是关于树的一些重要术语。
路径 − 路径指的是沿着树的边的一系列节点。
根 − 树顶部的节点称为根节点。每棵树只有一个根节点,并且从根节点到任何节点都只有一条路径。
父节点 − 除根节点外的任何节点都有一条向上连接到称为父节点的节点的边。
子节点 − 下面连接到给定节点并通过其向下边连接的节点称为其子节点。
叶子节点 − 没有子节点的节点称为叶子节点。
子树 − 子树表示节点的后代。
访问 − 访问指的是当控制权在节点上时检查节点的值。
遍历 − 遍历意味着以特定顺序通过节点。
层级 − 节点的层级表示节点的代数。如果根节点在第0层,则其子节点在第1层,其孙节点在第2层,依此类推。
键 − 键表示节点的值,基于该值将进行节点的搜索操作。
二叉搜索树表现出特殊的行为。节点的左子节点的值必须小于其父节点的值,而节点的右子节点的值必须大于其父节点的值。
二叉搜索树表示
我们将使用节点对象来实现树,并通过引用将它们连接起来。
基本操作
以下是树的基本主要操作:
搜索 − 在树中搜索一个元素。
插入 − 在树中插入一个元素。
前序遍历 − 以前序方式遍历树。
中序遍历 − 以中序方式遍历树。
后序遍历 − 以后序方式遍历树。
节点
定义一个节点,其中包含一些数据以及对其左右子节点的引用。
public class Node {
public int data;
public Node leftChild;
public Node rightChild;
public Node(){}
public void display(){
System.out.print("("+data+ ")");
}
}
搜索操作
每当需要搜索一个元素时,从根节点开始搜索。如果数据小于键值,则在左子树中搜索元素,否则在右子树中搜索元素。对每个节点遵循相同的算法。
public Node search(int data){
Node current = root;
System.out.print("Visiting elements: ");
while(current.data != data){
if(current != null)
System.out.print(current.data + " ");
//go to left tree
if(current.data > data){
current = current.leftChild;
}//else go to right tree
else{
current = current.rightChild;
}
//not found
if(current == null){
return null;
}
}
return current;
}
插入操作
每当需要插入一个元素时,首先找到其合适的位置。从根节点开始搜索,如果数据小于键值,则在左子树中搜索空位置并插入数据。否则,在右子树中搜索空位置并插入数据。
public void insert(int data){
Node tempNode = new Node();
tempNode.data = data;
//if tree is empty
if(root == null){
root = tempNode;
}else{
Node current = root;
Node parent = null;
while(true){
parent = current;
//go to left of the tree
if(data < parent.data){
current = current.leftChild;
//insert to the left
if(current == null){
parent.leftChild = tempNode;
return;
}
}//go to right of the tree
else{
current = current.rightChild;
//insert to the right
if(current == null){
parent.rightChild = tempNode;
return;
}
}
}
}
}
前序遍历
这是一个简单的三步过程。
访问根节点
遍历左子树
遍历右子树
private void preOrder(Node root){
if(root!=null){
System.out.print(root.data + " ");
preOrder(root.leftChild);
preOrder(root.rightChild);
}
}
中序遍历
这是一个简单的三步过程。
遍历左子树
访问根节点
遍历右子树
private void inOrder(Node root){
if(root!=null){
inOrder(root.leftChild);
System.out.print(root.data + " ");
inOrder(root.rightChild);
}
}
后序遍历
这是一个简单的三步过程。
遍历左子树
遍历右子树
访问根节点
private void postOrder(Node root){
if(root!=null){
postOrder(root.leftChild);
postOrder(root.rightChild);
System.out.print(root.data + " ");
}
}
树实现
Node.java
package com.tutorialspoint.datastructure;
public class Node {
public int data;
public Node leftChild;
public Node rightChild;
public Node(){}
public void display(){
System.out.print("("+data+ ")");
}
}
Tree.java
package com.tutorialspoint.datastructure;
public class Tree {
private Node root;
public Tree(){
root = null;
}
public Node search(int data){
Node current = root;
System.out.print("Visiting elements: ");
while(current.data != data){
if(current != null)
System.out.print(current.data + " ");
//go to left tree
if(current.data > data){
current = current.leftChild;
}//else go to right tree
else{
current = current.rightChild;
}
//not found
if(current == null){
return null;
}
}
return current;
}
public void insert(int data){
Node tempNode = new Node();
tempNode.data = data;
//if tree is empty
if(root == null){
root = tempNode;
}else{
Node current = root;
Node parent = null;
while(true){
parent = current;
//go to left of the tree
if(data < parent.data){
current = current.leftChild;
//insert to the left
if(current == null){
parent.leftChild = tempNode;
return;
}
}//go to right of the tree
else{
current = current.rightChild;
//insert to the right
if(current == null){
parent.rightChild = tempNode;
return;
}
}
}
}
}
public void traverse(int traversalType){
switch(traversalType){
case 1:
System.out.print("\nPreorder traversal: ");
preOrder(root);
break;
case 2:
System.out.print("\nInorder traversal: ");
inOrder(root);
break;
case 3:
System.out.print("\nPostorder traversal: ");
postOrder(root);
break;
}
}
private void preOrder(Node root){
if(root!=null){
System.out.print(root.data + " ");
preOrder(root.leftChild);
preOrder(root.rightChild);
}
}
private void inOrder(Node root){
if(root!=null){
inOrder(root.leftChild);
System.out.print(root.data + " ");
inOrder(root.rightChild);
}
}
private void postOrder(Node root){
if(root!=null){
postOrder(root.leftChild);
postOrder(root.rightChild);
System.out.print(root.data + " ");
}
}
}
演示程序
TreeDemo.java
package com.tutorialspoint.datastructure;
public class TreeDemo {
public static void main(String[] args){
Tree tree = new Tree();
/* 11 //Level 0
*/
tree.insert(11);
/* 11 //Level 0
* |
* |---20 //Level 1
*/
tree.insert(20);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
*/
tree.insert(3);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
*/
tree.insert(42);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
* |
* |--54 //Level 3
*/
tree.insert(54);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* |--54 //Level 3
*/
tree.insert(16);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
tree.insert(32);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
tree.insert(9);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--| 32--|--54 //Level 3
*/
tree.insert(4);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--|--10 32--|--54 //Level 3
*/
tree.insert(10);
Node node = tree.search(32);
if(node!=null){
System.out.print("Element found.");
node.display();
System.out.println();
}else{
System.out.println("Element not found.");
}
Node node1 = tree.search(2);
if(node1!=null){
System.out.println("Element found.");
node1.display();
System.out.println();
}else{
System.out.println("Element not found.");
}
//pre-order traversal
//root, left ,right
tree.traverse(1);
//in-order traversal
//left, root ,right
tree.traverse(2);
//post order traversal
//left, right, root
tree.traverse(3);
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Visiting elements: 11 20 42 Element found.(32) Visiting elements: 11 3 Element not found. Preorder traversal: 11 3 9 4 10 20 16 42 32 54 Inorder traversal: 3 4 9 10 11 16 20 32 42 54 Postorder traversal: 4 10 9 3 16 32 54 42 20 11
Java 数据结构与算法 - 哈希表
概述
哈希表是一种数据结构,其中插入和搜索操作速度非常快,与哈希表的大小无关。它几乎是常数时间或O(1)。哈希表使用数组作为存储介质,并使用哈希技术生成要插入元素或从中定位元素的索引。
哈希
哈希是一种将一系列键值转换为数组索引范围的技术。我们将使用模运算符来获取一系列键值。考虑一个大小为20的哈希表的示例,以及要存储的以下项。项采用(键,值)格式。
(1,20)
(2,70)
(42,80)
(4,25)
(12,44)
(14,32)
(17,11)
(13,78)
(37,98)
| 序号 | 键 | 哈希值 | 数组索引 |
|---|---|---|---|
| 1 | 1 | 1 % 20 = 1 | 1 |
| 2 | 2 | 2 % 20 = 2 | 2 |
| 3 | 42 | 42 % 20 = 2 | 2 |
| 4 | 4 | 4 % 20 = 4 | 4 |
| 5 | 12 | 12 % 20 = 12 | 12 |
| 6 | 14 | 14 % 20 = 14 | 14 |
| 7 | 17 | 17 % 20 = 17 | 17 |
| 8 | 13 | 13 % 20 = 13 | 13 |
| 9 | 37 | 37 % 20 = 17 | 17 |
线性探测
正如我们所看到的,使用的哈希技术可能会创建数组中已使用的索引。在这种情况下,我们可以通过查看下一个单元格,直到找到一个空单元格,从而在数组中搜索下一个空位置。这种技术称为线性探测。
| 序号 | 键 | 哈希值 | 数组索引 | 线性探测后,数组索引 |
|---|---|---|---|---|
| 1 | 1 | 1 % 20 = 1 | 1 | 1 |
| 2 | 2 | 2 % 20 = 2 | 2 | 2 |
| 3 | 42 | 42 % 20 = 2 | 2 | 3 |
| 4 | 4 | 4 % 20 = 4 | 4 | 4 |
| 5 | 12 | 12 % 20 = 12 | 12 | 12 |
| 6 | 14 | 14 % 20 = 14 | 14 | 14 |
| 7 | 17 | 17 % 20 = 17 | 17 | 17 |
| 8 | 13 | 13 % 20 = 13 | 13 | 13 |
| 9 | 37 | 37 % 20 = 17 | 17 | 18 |
基本操作
以下是哈希表的基本主要操作:
搜索 − 在哈希表中搜索一个元素。
插入 − 在哈希表中插入一个元素。
删除 − 从哈希表中删除一个元素。
数据项
定义一个数据项,其中包含一些数据和键,基于该键将在哈希表中进行搜索。
public class DataItem {
private int key;
private int data;
public DataItem(int key, int data){
this.key = key;
this.data = data;
}
public int getKey(){
return key;
}
public int getData(){
return data;
}
}
哈希方法
定义一个哈希方法来计算数据项键的哈希码。
public int hashCode(int key){
return key % size;
}
搜索操作
每当需要搜索一个元素时,计算传递的键的哈希码,并使用该哈希码作为数组中的索引来定位元素。如果在计算的哈希码处未找到元素,则使用线性探测来获取前面的元素。
public DataItem search(int key){
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=null){
if(hashArray[hashIndex].getKey() == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= size;
}
return null;
}
插入操作
每当需要插入一个元素时,计算传递的键的哈希码,并使用该哈希码作为数组中的索引来定位索引。如果在计算的哈希码处找到元素,则使用线性探测查找空位置。
public void insert(DataItem item){
int key = item.getKey();
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] !=null
&& hashArray[hashIndex].getKey() != -1){
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= size;
}
hashArray[hashIndex] = item;
}
删除操作
每当需要删除一个元素时,计算传递的键的哈希码,并使用该哈希码作为数组中的索引来定位索引。如果在计算的哈希码处未找到元素,则使用线性探测来获取前面的元素。找到后,在该处存储一个虚拟项以保持哈希表的性能不变。
public DataItem delete(DataItem item){
int key = item.getKey();
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=null){
if(hashArray[hashIndex].getKey() == key){
DataItem temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= size;
}
return null;
}
哈希表实现
DataItem.java
package com.tutorialspoint.datastructure;
public class DataItem {
private int key;
private int data;
public DataItem(int key, int data){
this.key = key;
this.data = data;
}
public int getKey(){
return key;
}
public int getData(){
return data;
}
}
HashTable.java
package com.tutorialspoint.datastructure;
public class HashTable {
private DataItem[] hashArray;
private int size;
private DataItem dummyItem;
public HashTable(int size){
this.size = size;
hashArray = new DataItem[size];
dummyItem = new DataItem(-1,-1);
}
public void display(){
for(int i=0; i<size; i++) {
if(hashArray[i] != null)
System.out.print(" ("
+hashArray[i].getKey()+","
+hashArray[i].getData() + ") ");
else
System.out.print(" ~~ ");
}
System.out.println("");
}
public int hashCode(int key){
return key % size;
}
public DataItem search(int key){
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=null){
if(hashArray[hashIndex].getKey() == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= size;
}
return null;
}
public void insert(DataItem item){
int key = item.getKey();
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] !=null
&& hashArray[hashIndex].getKey() != -1){
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= size;
}
hashArray[hashIndex] = item;
}
public DataItem delete(DataItem item){
int key = item.getKey();
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=null){
if(hashArray[hashIndex].getKey() == key){
DataItem temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= size;
}
return null;
}
}
演示程序
HashTableDemo.java
package com.tutorialspoint.datastructure;
public class HashTableDemo {
public static void main(String[] args){
HashTable hashTable = new HashTable(20);
hashTable.insert(new DataItem(1, 20));
hashTable.insert(new DataItem(2, 70));
hashTable.insert(new DataItem(42, 80));
hashTable.insert(new DataItem(4, 25));
hashTable.insert(new DataItem(12, 44));
hashTable.insert(new DataItem(14, 32));
hashTable.insert(new DataItem(17, 11));
hashTable.insert(new DataItem(13, 78));
hashTable.insert(new DataItem(37, 97));
hashTable.display();
DataItem item = hashTable.search(37);
if(item != null){
System.out.println("Element found: "+ item.getData());
}else{
System.out.println("Element not found");
}
hashTable.delete(item);
item = hashTable.search(37);
if(item != null){
System.out.println("Element found: "+ item.getData());
}else{
System.out.println("Element not found");
}
}
}
如果我们编译并运行上述程序,则会产生以下结果:
~~ (1,20) (2,70) (42,80) (4,25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12,44) (13,78) (14,32) ~~ ~~ (17,11) (37,97) ~~ Element found: 97 Element not found
Java 数据结构与算法 - 堆
概述
堆是一种特殊基于树的数据结构,用于表示优先队列或用于堆排序。我们将专门讨论二叉堆。
二叉堆可以分为具有两个约束条件的二叉树:
完全性 − 二叉堆是一个完全二叉树,除了最后一层可能并非所有元素都存在,但元素应从左到右填充。
堆性 − 所有父节点都应大于或小于其子节点。如果父节点大于其子节点,则称为最大堆,否则称为最小堆。最大堆用于堆排序,最小堆用于优先队列。我们考虑最小堆,并将使用数组实现。
基本操作
以下是最小堆的基本主要操作:
插入 − 在堆中插入一个元素。
获取最小值 − 从堆中获取最小元素。
移除最小值 − 从堆中移除最小元素
插入操作
每当需要插入一个元素时,将元素插入到数组的末尾。将堆的大小增加1。
- 当堆属性被破坏时,向上调整元素。将元素与其父节点的值进行比较,如果需要则交换它们。
public void insert(int value) {
size++;
intArray[size - 1] = value;
heapUp(size - 1);
}
private void heapUp(int nodeIndex){
int parentIndex, tmp;
if (nodeIndex != 0) {
parentIndex = getParentIndex(nodeIndex);
if (intArray[parentIndex] > intArray[nodeIndex]) {
tmp = intArray[parentIndex];
intArray[parentIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapUp(parentIndex);
}
}
}
获取最小值
获取实现堆的数组的第一个元素,该元素为根。
public int getMinimum(){
return intArray[0];
}
移除最小值
每当需要移除一个元素时,获取数组的最后一个元素,并将堆的大小减少1。
- 当堆属性被破坏时,向下调整元素。将元素与其子节点的值进行比较,如果需要则交换它们。
public void removeMin() {
intArray[0] = intArray[size - 1];
size--;
if (size > 0)
heapDown(0);
}
private void heapDown(int nodeIndex){
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= size) {
if (leftChildIndex >= size)
return;
else
minIndex = leftChildIndex;
} else {
if (intArray[leftChildIndex] <= intArray[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (intArray[nodeIndex] > intArray[minIndex]) {
tmp = intArray[minIndex];
intArray[minIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapDown(minIndex);
}
}
堆实现
Heap.java
package com.tutorialspoint.datastructure;
public class Heap {
private int[] intArray;
private int size;
public Heap(int size){
intArray = new int[size];
}
public boolean isEmpty(){
return size == 0;
}
public int getMinimum(){
return intArray[0];
}
public int getLeftChildIndex(int nodeIndex){
return 2*nodeIndex +1;
}
public int getRightChildIndex(int nodeIndex){
return 2*nodeIndex +2;
}
public int getParentIndex(int nodeIndex){
return (nodeIndex -1)/2;
}
public boolean isFull(){
return size == intArray.length;
}
public void insert(int value) {
size++;
intArray[size - 1] = value;
heapUp(size - 1);
}
public void removeMin() {
intArray[0] = intArray[size - 1];
size--;
if (size > 0)
heapDown(0);
}
/**
* Heap up the new element,until heap property is broken.
* Steps:
* 1. Compare node's value with parent's value.
* 2. Swap them, If they are in wrong order.
* */
private void heapUp(int nodeIndex){
int parentIndex, tmp;
if (nodeIndex != 0) {
parentIndex = getParentIndex(nodeIndex);
if (intArray[parentIndex] > intArray[nodeIndex]) {
tmp = intArray[parentIndex];
intArray[parentIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapUp(parentIndex);
}
}
}
/**
* Heap down the root element being least in value,until heap property is broken.
* Steps:
* 1.If current node has no children, done.
* 2.If current node has one children and heap property is broken,
* 3.Swap the current node and child node and heap down.
* 4.If current node has one children and heap property is broken, find smaller one
* 5.Swap the current node and child node and heap down.
* */
private void heapDown(int nodeIndex){
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= size) {
if (leftChildIndex >= size)
return;
else
minIndex = leftChildIndex;
} else {
if (intArray[leftChildIndex] <= intArray[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (intArray[nodeIndex] > intArray[minIndex]) {
tmp = intArray[minIndex];
intArray[minIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapDown(minIndex);
}
}
}
演示程序
HeapDemo.java
package com.tutorialspoint.datastructure;
public class HeapDemo {
public static void main(String[] args){
Heap heap = new Heap(10);
/* 5 //Level 0
*
*/
heap.insert(5);
/* 1 //Level 0
* |
* 5---| //Level 1
*/
heap.insert(1);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
*/
heap.insert(3);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* |
* 8--| //Level 2
*/
heap.insert(8);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* |
* 8--|--9 //Level 2
*/
heap.insert(9);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* | |
* 8--|--9 6--| //Level 2
*/
heap.insert(6);
/* 1 //Level 0
* |
* 5---|---2 //Level 1
* | |
* 8--|--9 6--|--3 //Level 2
*/
heap.insert(2);
System.out.println(heap.getMinimum());
heap.removeMin();
/* 2 //Level 0
* |
* 5---|---3 //Level 1
* | |
* 8--|--9 6--| //Level 2
*/
System.out.println(heap.getMinimum());
}
}
如果我们编译并运行上述程序,则会产生以下结果:
1 2
Java 数据结构与算法 - 图
概述
图是一种用于模拟数学图的数据结构。它由一组称为顶点的边的连接对组成。我们可以使用顶点数组和二维边数组来表示图。
重要术语
顶点 − 图的每个节点都表示为一个顶点。在下面给出的示例中,带标签的圆圈代表顶点。因此,A 到 G 都是顶点。我们可以使用数组来表示它们,如下面的图像所示。这里 A 可以用索引 0 来标识。B 可以用索引 1 来标识,以此类推。
边 − 边表示两个顶点之间的路径或两个顶点之间的线。在下面给出的示例中,从 A 到 B、从 B 到 C 等的线表示边。我们可以使用二维数组来表示数组,如下面的图像所示。这里 AB 可以用第 0 行第 1 列的 1 来表示,BC 可以用第 1 行第 2 列的 1 来表示,以此类推,其他组合则为 0。
邻接 − 如果两个节点或顶点通过一条边连接在一起,则它们是邻接的。在下面给出的示例中,B 与 A 邻接,C 与 B 邻接,以此类推。
路径 − 路径表示两个顶点之间的一系列边。在下面给出的示例中,ABCD 表示从 A 到 D 的一条路径。
基本操作
以下是图的基本主要操作。
添加顶点 − 向图中添加一个顶点。
添加边 − 在图的两个顶点之间添加一条边。
显示顶点 − 显示图的一个顶点。
添加顶点操作
//add vertex to the array of vertex
public void addVertex(char label){
lstVertices[vertexCount++] = new Vertex(label);
}
添加边操作
//add edge to edge array
public void addEdge(int start,int end){
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
显示边操作
//display the vertex
public void displayVertex(int vertexIndex){
System.out.print(lstVertices[vertexIndex].label+" ");
}
遍历算法
以下是图上重要的遍历算法。
深度优先搜索 − 以深度优先的方式遍历图。
广度优先搜索 − 以广度优先的方式遍历图。
深度优先搜索算法
深度优先搜索算法 (DFS) 以深度优先的方式遍历图,并使用堆栈来记住当任何迭代中出现死胡同时要开始搜索的下一个顶点。
如上例所示,DFS 算法首先从 A 遍历到 B、C、D,然后到 E,然后到 F,最后到 G。它采用以下规则。
规则 1 − 访问相邻的未访问顶点。标记为已访问。显示它。将其压入堆栈。
规则 2 − 如果未找到相邻顶点,则从堆栈中弹出顶点。(它将弹出堆栈中所有没有相邻顶点的顶点。)
规则 3 − 重复规则 1 和规则 2,直到堆栈为空。
public void depthFirstSearch(){
//mark first node as visited
lstVertices[0].visited = true;
//display the vertex
displayVertex(0);
//push vertex index in stack
stack.push(0);
while(!stack.isEmpty()){
//get the unvisited vertex of vertex which is at top of the stack
int unvisitedVertex = getAdjUnvisitedVertex(stack.peek());
//no adjacent vertex found
if(unvisitedVertex == -1){
stack.pop();
}else{
lstVertices[unvisitedVertex].visited = true;
displayVertex(unvisitedVertex);
stack.push(unvisitedVertex);
}
}
//stack is empty, search is complete, reset the visited flag
for(int i=0;i<vertexCount;i++){
lstVertices[i].visited = false;
}
}
广度优先搜索算法
广度优先搜索算法 (BFS) 以广度优先的方式遍历图,并使用队列来记住当任何迭代中出现死胡同时要开始搜索的下一个顶点。
如上例所示,BFS 算法首先从 A 遍历到 B、E、F,然后到 C 和 G,最后到 D。它采用以下规则。
规则 1 − 访问相邻的未访问顶点。标记为已访问。显示它。将其插入队列。
规则 2 − 如果未找到相邻顶点,则从队列中移除第一个顶点。
规则 3 − 重复规则 1 和规则 2,直到队列为空。
public void breadthFirstSearch(){
//mark first node as visited
lstVertices[0].visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
queue.insert(0);
int unvisitedVertex;
while(!queue.isEmpty()){
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = queue.remove();
//no adjacent vertex found
while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){
lstVertices[unvisitedVertex].visited = true;
displayVertex(unvisitedVertex);
queue.insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(int i=0;i<vertexCount;i++){
lstVertices[i].visited = false;
}
}
图的实现
Stack.java
package com.tutorialspoint.datastructure;
public class Stack {
private int size; // size of the stack
private int[] intArray; // stack storage
private int top; // top of the stack
// Constructor
public Stack(int size){
this.size = size;
intArray = new int[size]; //initialize array
top = -1; //stack is initially empty
}
// Operation : Push
// push item on the top of the stack
public void push(int data) {
if(!isFull()){
// increment top by 1 and insert data
intArray[++top] = data;
}else{
System.out.println("Cannot add data. Stack is full.");
}
}
// Operation : Pop
// pop item from the top of the stack
public int pop() {
//retrieve data and decrement the top by 1
return intArray[top--];
}
// Operation : Peek
// view the data at top of the stack
public int peek() {
//retrieve data from the top
return intArray[top];
}
// Operation : isFull
// return true if stack is full
public boolean isFull(){
return (top == size-1);
}
// Operation : isEmpty
// return true if stack is empty
public boolean isEmpty(){
return (top == -1);
}
}
Queue.java
package com.tutorialspoint.datastructure;
public class Queue {
private final int MAX;
private int[] intArray;
private int front;
private int rear;
private int itemCount;
public Queue(int size){
MAX = size;
intArray = new int[MAX];
front = 0;
rear = -1;
itemCount = 0;
}
public void insert(int data){
if(!isFull()){
if(rear == MAX-1){
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
public int remove(){
int data = intArray[front++];
if(front == MAX){
front = 0;
}
itemCount--;
return data;
}
public int peek(){
return intArray[front];
}
public boolean isEmpty(){
return itemCount == 0;
}
public boolean isFull(){
return itemCount == MAX;
}
public int size(){
return itemCount;
}
}
Vertex.java
package com.tutorialspoint.datastructure;
public class Vertex {
public char label;
public boolean visited;
public Vertex(char label){
this.label = label;
visited = false;
}
}
Graph.java
package com.tutorialspoint.datastructure;
public class Graph {
private final int MAX = 20;
//array of vertices
private Vertex lstVertices[];
//adjacency matrix
private int adjMatrix[][];
//vertex count
private int vertexCount;
private Stack stack;
private Queue queue;
public Graph(){
lstVertices = new Vertex[MAX];
adjMatrix = new int[MAX][MAX];
vertexCount = 0;
stack = new Stack(MAX);
queue = new Queue(MAX);
for(int j=0; j<MAX; j++) // set adjacency
for(int k=0; k<MAX; k++) // matrix to 0
adjMatrix[j][k] = 0;
}
//add vertex to the vertex list
public void addVertex(char label){
lstVertices[vertexCount++] = new Vertex(label);
}
//add edge to edge array
public void addEdge(int start,int end){
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
public void displayVertex(int vertexIndex){
System.out.print(lstVertices[vertexIndex].label+" ");
}
//get the adjacent unvisited vertex
public int getAdjUnvisitedVertex(int vertexIndex){
for(int i=0; i<vertexCount; i++)
if(adjMatrix[vertexIndex][i]==1 && lstVertices[i].visited==false)
return i;
return -1;
}
public void depthFirstSearch(){
//mark first node as visited
lstVertices[0].visited = true;
//display the vertex
displayVertex(0);
//push vertex index in stack
stack.push(0);
while(!stack.isEmpty()){
//get the unvisited vertex of vertex which is at top of the stack
int unvisitedVertex = getAdjUnvisitedVertex(stack.peek());
//no adjacent vertex found
if(unvisitedVertex == -1){
stack.pop();
}else{
lstVertices[unvisitedVertex].visited = true;
displayVertex(unvisitedVertex);
stack.push(unvisitedVertex);
}
}
//stack is empty, search is complete, reset the visited flag
for(int i=0;i<vertexCount;i++){
lstVertices[i].visited = false;
}
}
public void breadthFirstSearch(){
//mark first node as visited
lstVertices[0].visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
queue.insert(0);
int unvisitedVertex;
while(!queue.isEmpty()){
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = queue.remove();
//no adjacent vertex found
while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){
lstVertices[unvisitedVertex].visited = true;
displayVertex(unvisitedVertex);
queue.insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(int i=0;i<vertexCount;i++){
lstVertices[i].visited = false;
}
}
}
演示程序
GraphDemo.java
package com.tutorialspoint.datastructure;
public class GraphDemo {
public static void main(String args[]){
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
/* 1 2 3
* 0 |--B--C--D
* A--|
* |
* | 4
* |-----E
* | 5 6
* | |--F--G
* |--|
*/
graph.addEdge(0, 1); //AB
graph.addEdge(1, 2); //BC
graph.addEdge(2, 3); //CD
graph.addEdge(0, 4); //AC
graph.addEdge(0, 5); //AF
graph.addEdge(5, 6); //FG
System.out.print("Depth First Search: ");
//A B C D E F G
graph.depthFirstSearch();
System.out.println("");
System.out.print("Breadth First Search: ");
//A B E F C G D
graph.breadthFirstSearch();
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Depth First Search: A B C D E F G Breadth First Search: A B E F C G D
Java 数据结构与算法 - 搜索技术
搜索是指在项目集合中找到具有指定属性的所需元素。我们将使用以下常用且简单的搜索算法开始我们的讨论。
| 序号 | 技术与描述 |
|---|---|
| 1 | 线性搜索 线性搜索搜索所有项目,其最坏执行时间为 n,其中 n 是项目数。 |
| 2 | 二分搜索 二分搜索要求项目按排序顺序排列,但其最坏执行时间是恒定的,并且比线性搜索快得多。 |
| 3 | 插值搜索 插值搜索要求项目按排序顺序排列,但其最坏执行时间为 O(n),其中 n 是项目数,并且它比线性搜索快得多。 |
Java 数据结构与算法 - 排序技术
排序是指以特定格式排列数据。排序算法指定以特定顺序排列数据的方式。最常见的顺序是数字顺序或字典顺序。
排序的重要性在于,如果数据以排序方式存储,则可以将数据搜索优化到非常高的水平。排序还用于以更易读的格式表示数据。现实生活中排序的一些示例如下。
电话簿 − 电话簿按姓名对人员的电话号码进行排序。以便可以搜索姓名。
字典 − 字典按字母顺序排列单词,以便任何工作的搜索变得容易。
排序类型
以下是流行的排序算法及其比较列表。
| 序号 | 技术与描述 |
|---|---|
| 1 | 冒泡排序 冒泡排序易于理解和实现,但性能非常差。 |
| 2 | 选择排序 选择排序顾名思义,使用选择所需项目并相应地准备排序数组的技术。 |
| 3 | 插入排序 插入排序是选择排序的一种变体。 |
| 4 | 希尔排序 希尔排序是插入排序的有效版本。 |
| 5 | 快速排序 快速排序是一种高效的排序算法,基于将数据数组划分为更小的数组。 |
| 6 | 排序对象
可以使用 java.util.Arrays.sort()轻松排序 Java 对象。 |
Java 数据结构与算法 - 递归
概述
递归是指编程语言中一种函数调用自身的技术。调用自身的函数称为递归方法。
特点
递归函数必须具有以下两个特征
基本情况
一系列规则,这些规则在减少情况后会导致基本情况。
递归阶乘
阶乘是递归的经典示例之一。阶乘是一个满足以下条件的非负数。
0! = 1
1! = 1
n! = n * n-1!
阶乘用“!”表示。这里规则 1 和规则 2 是基本情况,规则 3 是阶乘规则。
例如,3! = 3 x 2 x 1 = 6
private int factorial(int n){
//base case
if(n == 0){
return 1;
}else{
return n * factorial(n-1);
}
}
递归斐波那契数列
斐波那契数列是递归的另一个经典示例。斐波那契数列是一系列满足以下条件的整数。
F0 = 0
F1 = 1
Fn = Fn-1 + Fn-2
斐波那契用“F”表示。这里规则 1 和规则 2 是基本情况,规则 3 是斐波那契规则。
例如,F5 = 0 1 1 2 3
演示程序
RecursionDemo.java
package com.tutorialspoint.algorithm;
public class RecursionDemo {
public static void main(String[] args){
RecursionDemo recursionDemo = new RecursionDemo();
int n = 5;
System.out.println("Factorial of " + n + ": "
+ recursionDemo.factorial(n));
System.out.print("Fibbonacci of " + n + ": ");
for(int i=0;i<n;i++){
System.out.print(recursionDemo.fibbonacci(i) +" ");
}
}
private int factorial(int n){
//base case
if(n == 0){
return 1;
}else{
return n * factorial(n-1);
}
}
private int fibbonacci(int n){
if(n ==0){
return 0;
}
else if(n==1){
return 1;
}
else {
return (fibbonacci(n-1) + fibbonacci(n-2));
}
}
}
如果我们编译并运行上述程序,则会产生以下结果:
Factorial of 5: 120 Fibbonacci of 5: 0 1 1 2 3