示波器探头

我们可以通过探头将任何测试电路连接到示波器。由于示波器（CRO）是一种基本的示波器，因此连接到它的探头也称为**示波器探头**。

我们应该选择探头，使其不会对测试电路造成任何负载问题。这样我们就可以在示波器屏幕上正确地分析测试电路的信号。

示波器探头应具有以下**特性**。

示波器探头的**框图**如下所示。

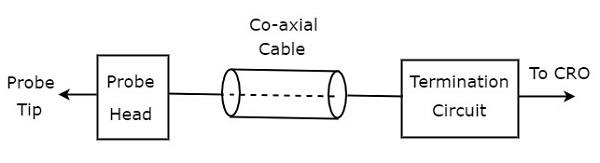
如图所示，示波器探头主要由三个部分组成。分别是探头头、同轴电缆和终端电路。同轴电缆简单地连接探头头和终端电路。

示波器探头的类型

示波器探头可以分为以下**两种类型**。

现在，让我们逐一讨论这两种类型的探头。

如果探头头由无源元件组成，则称为**无源探头**。无源探头的电路图如下所示。

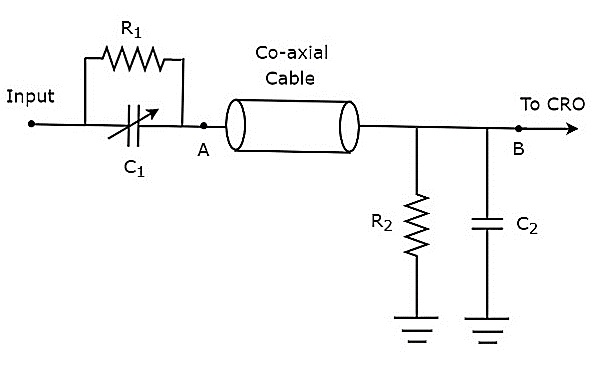
如图所示，探头头由电阻R₁和可变电容C₁的并联组合组成。类似地，终端电路由电阻R₂和电容C₂的并联组合组成。

上述电路图以**桥式电路**的形式修改，如下所示。

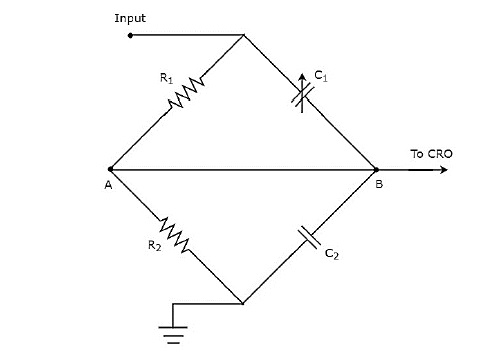
通过调整可变电容C₁的值，我们可以平衡桥路。我们将在后面的章节中讨论桥式电路的概念。目前，请考虑以下**交流桥的平衡条件**。

$$Z_{1}Z_{4}=Z_{2}Z_{3}$$

**代入**阻抗Z₁、Z₂、Z₃和Z₄分别为R₁、1/(jωC₁)、R₂和1/(jωC₂)到上式中。

$$R_{1}\left ( \frac{1}{j \omega C_{2}} \right )=\left ( \frac{1}{j \omega C_{1}} \right )R_{2}$$

$\Rightarrow R_{1} C_{1}=R_{2} C_{2}$公式1

根据分压原理，我们可以得到**电阻R₂上的电压**为

$$V_{0}=V_{i}\left ( \frac{R_{2}}{R_{1}+R_{2}} \right )$$

**衰减系数**是输入电压V_i与输出电压V₀的比值。因此，从上式中我们可以得到衰减系数α为

$$\alpha = \frac{V_{i}}{V_{0}}=\frac{R_{1}+R_{2}}{R_{2}}$$

$\Rightarrow \alpha = 1+\frac{R_{1}}{R_{2}}$

$\Rightarrow \alpha-1 = \frac{R_{1}}{R_{2}}$

$\Rightarrow R_{1}= \left ( \alpha-1 \right )R_{2}$公式2

从公式2可以得出，对于α>1的整数，R₁的值大于或等于R₂的值。

将公式2代入公式1。

$$\left ( \alpha-1 \right )R_{2}C_{1}=R_{2}C_{2}$$

$\Rightarrow \left ( \alpha-1 \right )C_{1} =C_{2}$

$\Rightarrow C_{1}=\frac{C_{2}}{\left ( \alpha-1 \right )}$公式3

从公式3可以得出，对于α>1的整数，C₁的值小于或等于C₂的值。

示例

让我们找到衰减系数α为10的探头的R₁和C₁的值。假设R₂=1MΩ，C₂=18pF。

$$ R_{1}=\left ( 10-1 \right )\times 1 \times 10^{6}$$

$$\Rightarrow R_{1}=9 \times 10^{6}$$

$$\Rightarrow R_{1}=9 M\Omega$$

**步骤2** - 我们将通过将α和C₂的值代入公式3来得到C₁的值。

$$C_{1}=\frac{18\times10^{-12}}{\left ( 10-1 \right )}$$

$$\Rightarrow C_{1}=2 \times 10^{-12}$$

$$\Rightarrow C_{1}=2 pF$$

因此，对于给定的规格，探头的R₁和C₁的值将分别为9MΩ和2pF。

如果探头头由有源电子元件组成，则称为**有源探头**。有源探头的框图如下所示。

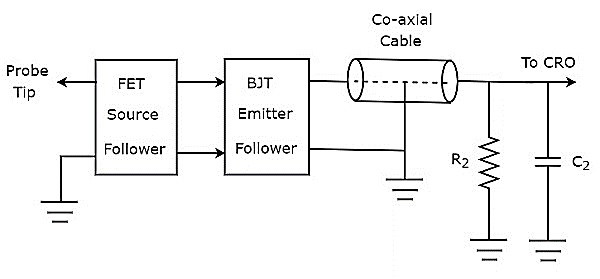
如图所示，探头头由级联的FET源跟随器和BJT发射极跟随器组成。FET源跟随器提供高输入阻抗和低输出阻抗。而BJT发射极跟随器的目的是避免或消除阻抗失配。

其他两个部分，如同轴电缆和终端电路，在有源探头和无源探头中保持相同。

打印页面