快速指南

---

---

引言

用于测量任何量的仪器称为测量仪器。本教程主要介绍电子仪器，这些仪器可用于测量电量或参数。

以下是最常用的电子仪器。

• 电压表
• 电流表
• 欧姆表
• 万用表

现在，让我们简要讨论一下这些仪器。

电压表

顾名思义，电压表是一种测量仪器，用于测量电路任意两点之间的电压。电压表有两种类型：直流电压表和交流电压表。

直流电压表测量电路任意两点之间的直流电压，而交流电压表测量电路任意两点之间的交流电压。下图显示了一个实际直流电压表的示例。

上图所示的直流电压表是(0-100)V 直流电压表。因此，它可以用来测量从零伏到10伏的直流电压。

电流表

顾名思义，电流表是一种测量仪器，用于测量流过电路任意两点之间的电流。电流表有两种类型：直流电流表和交流电流表。

直流电流表测量流过电路任意两点之间的直流电流。而交流电流表测量流过电路任意两点之间的交流电流。下图显示了一个实际交流电流表的示例：

上图所示的交流电流表是(0-100)A 交流电流表。因此，它可以用来测量从零安培到100安培的交流电流。

欧姆表

欧姆表用于测量电路任意两点之间的电阻值。它也可用于查找未知电阻的值。欧姆表有两种类型：串联欧姆表和并联欧姆表。

在串联型欧姆表中，需要测量其值的未知电阻应与欧姆表串联连接。它适用于测量高电阻值。

在并联型欧姆表中，需要测量其值的未知电阻应与欧姆表并联连接。它适用于测量低电阻值。

上图显示了一个实际并联欧姆表的示例。上图所示的欧姆表是(0-100)Ω 并联欧姆表。因此，它可以用来测量从零欧姆到100欧姆的电阻值。

万用表

万用表是一种电子仪器，用于一次测量电压、电流和电阻等量。它可以用来测量不同范围的直流和交流电压、直流和交流电流以及电阻。下图显示了一个实际万用表：

如图所示，此万用表可用于测量各种高电阻、低电阻、直流电压、交流电压、直流电流和交流电流。上图标出了这些量不同的刻度和范围值。

本章中我们考虑的仪器属于指示型仪器，因为这些仪器的指针会偏转并指向特定值。我们将在后面的章节中详细讨论这些电子测量仪器。

性能特性

有助于了解仪器性能并帮助测量任何量或参数的测量仪器的特性称为性能特性。

性能特性的类型

仪器的性能特性可以分为以下两种类型。

• 静态特性
• 动态特性

现在，让我们逐一讨论这两种特性。

静态特性

测量仪器中不随时间变化的量或参数的特性称为静态特性。有时，这些量或参数可能会随时间缓慢变化。以下是静态特性的列表。

• 准确度
• 精密度
• 灵敏度
• 分辨率
• 静态误差

现在，让我们逐一讨论这些静态特性。

准确度

仪器的指示值 $A_{i}$ 与真值 $A_{t}$ 之间的代数差称为准确度。数学上，它可以表示为：

$$Accuracy = A_{i}- A_{t}$$

术语“准确度”表示仪器的指示值 $A_{i}$ 与真值 $A_{t}$ 的接近程度。

静态误差

不随时间变化的量的真值 $A_{t}$ 与仪器的指示值 $A_{i}$ 之间的差值称为静态误差 $e_{s}$。数学上，它可以表示为：

$$e_{s}= A_{t}- A_{i}$$

术语“静态误差”表示仪器的误差。如果静态误差用百分比表示，则称为静态误差百分比。数学上，它可以表示为：

$$\% e_{s}=\frac{e_{s}}{A_{t}}\times 100$$

将 $e_{s}$ 的值代入上述等式的右侧：

$$\% e_{s}=\frac{A_{t}- A_{i}}{A_{t}}\times 100$$

其中，

$\% e_{s}$ 是静态误差百分比。

精密度

如果仪器在相同情况下多次用于测量同一量时反复指示相同的值，则我们可以说该仪器具有较高的精密度。

灵敏度

仪器输出变化量 $\Delta A_{out}$ 与待测输入变化量 $\Delta A_{in}$ 之比称为灵敏度 S。数学上，它可以表示为：

$$S=\frac{\Delta A_{out}}{\Delta A_{in}}$$

术语“灵敏度”表示仪器响应所需的被测输入的最小变化。

• 如果校准曲线为线性，则仪器的灵敏度将为常数，等于校准曲线的斜率。

• 如果校准曲线为非线性，则仪器的灵敏度将不是常数，并且会随输入而变化。

分辨率

如果仪器的输出仅在输入有特定增量时才会发生变化，则该输入增量称为分辨率。这意味着，当输入有分辨率时，仪器能够有效地测量输入。

动态特性

用于测量随时间变化非常快的量或参数的仪器的特性称为动态特性。以下是动态特性的列表。

• 响应速度
• 动态误差
• 保真度
• 滞后

现在，让我们逐一讨论这些动态特性。

响应速度

每当待测量发生变化时，仪器响应的速度称为响应速度。它表示仪器的速度有多快。

滞后

每当待测量发生变化时，仪器响应中存在的延迟量称为测量滞后。它也简称为滞后。

动态误差

随时间变化的量的真值 $A_{t}$ 与仪器的指示值 $A_{i}$ 之间的差值称为动态误差 $e_{d}$。

保真度

仪器在没有任何动态误差的情况下指示被测量变化的程度称为保真度

电子测量仪器 - 误差

测量过程中出现的误差称为测量误差。在本章中，让我们讨论测量误差的类型。

测量误差的类型

我们可以将测量误差分为以下三种类型。

• 粗差
• 随机误差
• 系统误差

现在，让我们逐一讨论这三种测量误差。

粗差

观察者在获取测量值时由于缺乏经验而发生的误差称为粗差。粗差的值因观察者而异。有时，粗差也可能由于仪器选择不当而发生。我们可以通过以下两个步骤将粗差降到最低。

• 根据待测量的值范围选择最合适的仪器。
• 仔细记录读数

系统误差

如果仪器产生的误差在其运行过程中始终存在恒定的均匀偏差，则称为系统误差。系统误差是由于仪器中使用的材料的特性造成的。

系统误差的类型

系统误差可以分为以下三种类型。

• 仪器误差 - 这种误差是由于仪器的缺陷和负载效应造成的。

• 环境误差 - 这种误差是由于环境变化造成的，例如温度、压力等变化。

• 观察误差 - 这种误差是观察者在获取仪表读数时造成的。视差误差属于此类误差。

随机误差

在测量期间由于未知来源引起的误差称为**随机误差**。因此，不可能消除或最小化这些误差。但是，如果我们想获得没有任何随机误差的更准确的测量值，则可以通过以下两个步骤实现。

• **步骤1** - 由不同的观察者进行更多次数的读数。

• **步骤2** - 对步骤1中获得的读数进行统计分析。

以下是统计分析中使用的参数。

• 平均值
• 中位数
• 方差
• 偏差
• 标准差

现在，让我们讨论一下这些**统计参数**。

平均值

设$x_{1},x_{2},x_{3},....,x_{N}$是特定测量的$N$个读数。可以使用以下公式计算这些读数的平均值或**平均值**。

$$m = \frac{x_{1}+x_{2}+x_{3}+....+x_{N}}{N}$$

其中，$m$是平均值或平均值。

如果特定测量的读数数量较多，则平均值或平均值将近似等于**真值**。

中位数

如果特定测量的读数数量较多，则计算平均值或平均值比较困难。这里，计算**中位数**，它将近似等于平均值。

为了计算中位数，首先必须将特定测量的读数按**升序**排列。当读数个数为**奇数**时，可以使用以下公式计算中位数。

$$M=x_{\left ( \frac{N+1}{2} \right )}$$

当读数个数为**偶数**时，可以使用以下公式计算中位数。

$$M=\frac{x_{\left ( N/2 \right )}+x_\left ( \left [ N/2 \right ]+1 \right )}{2}$$

与平均值的偏差

特定测量值的读数与平均值之间的差值称为与平均值的偏差。简而言之，称为偏差。在数学上，它可以表示为

$$d_{i}=x_{i}-m$$

其中，

$d_{i}$是第$i$个读数与平均值的偏差。

$x_{i}$是第$i$个读数的值。

$m$是平均值或平均值。

标准差

偏差的均方根称为**标准差**。在数学上，它可以表示为

$$\sigma =\sqrt{\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N}}$$

如果读数个数N大于或等于20，则上述公式有效。当读数个数N小于20时，可以使用以下标准差公式。

$$\sigma =\sqrt{\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N-1}}$$

其中，

$\sigma$是标准差

$d_{1}, d_{2}, d_{3}, …, d_{N}$分别是第一、第二、第三、…、第$N$个读数与平均值的偏差。

**注意** - 如果标准差的值较小，则测量读数值的精度会更高。

方差

标准差的平方称为**方差**。在数学上，它可以表示为

$$V=\sigma^{2}$$

其中，

$V$是方差

$\sigma$是标准差

偏差的均方也称为**方差**。在数学上，它可以表示为

$$V=\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N}$$

如果读数个数N大于或等于20，则上述公式有效。当读数个数N小于20时，可以使用以下方差公式。

$$V=\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N-1}$$

其中，

$V$是方差

$d_{1}, d_{2}, d_{3}, …, d_{N}$分别是第一、第二、第三、…、第$N$个读数与平均值的偏差。

因此，借助统计参数，我们可以分析特定测量的读数。这样，我们将获得更准确的测量值。

电子测量仪器

用于测量任何量的仪器称为**测量仪器**。如果仪器可以测量基本的电量，例如电压和电流，则称为**基本测量仪器**。

基本测量仪器的类型

我们可以将基本测量仪器分为以下两种类型。

• 电压表
• 电流表

让我们简要讨论一下这两种基本测量仪器。

电压表

顾名思义，**电压表**是一种测量电路中任意两点之间电压的测量仪器。电压的单位是伏特，测量仪器是表。因此，单词“电压表”是由两个单词**“伏特”**和**“表”**组合而成。

我们可以根据其可以测量的电压类型将电压表分为以下**两种类型**。

• 直流电压表
• 交流电压表

直流电压表

顾名思义，直流电压表测量电路中任意两点之间的**直流电压**。下图显示了一个实际的直流电压表。

图中所示的直流电压表是**(0-10)V直流电压表**。因此，它可以用来测量从零伏特到10伏特的直流电压。

交流电压表

顾名思义，交流电压表测量电路中任意两点之间的**交流电压**。下图显示了一个实际的交流电压表。

上图所示的交流电压表是**(0-250)V交流电压表**。因此，它可以用来测量从零伏特到250伏特的交流电压。

电流表

顾名思义，**电流表**是一种测量流过电路中任意两点电流的测量仪器。电流的单位是安培，测量仪器是表。单词“电流表”是由安培的**“安”**与**“表”**组合而成。

我们可以根据其可以测量的电流类型将电流表分为以下**两种类型**。

• 直流电流表
• 交流电流表

直流电流表

顾名思义，直流电流表测量流过电路中任意两点之间的**直流电流**。下图显示了一个实际的直流电流表。

上图所示的直流电流表是**(0-50)A直流电流表**。因此，它可以用来测量从零安培到50安培的直流电流。

交流电流表

顾名思义，交流电流表测量流过电路中任意两点之间的**交流电流**。下图显示了一个实际的交流电流表。

上图所示的交流电流表是**(0-100)A交流电流表**。因此，它可以用来测量从零安培到100安培的交流电流。

我们将在接下来的几章中详细讨论各种电压表和电流表。

直流电压表

直流电压表是一种测量仪器，用于测量电路中任意两点之间的直流电压。如果我们将一个电阻与永磁移动线圈(PMMC)检流计串联，则整个组合一起充当**直流电压表**。

直流电压表中使用的串联电阻也称为串联倍增电阻或简称倍增器。它基本上限制了流过检流计的电流量，以防止仪表电流超过满刻度偏转值。直流电压表的**电路图**如下所示。

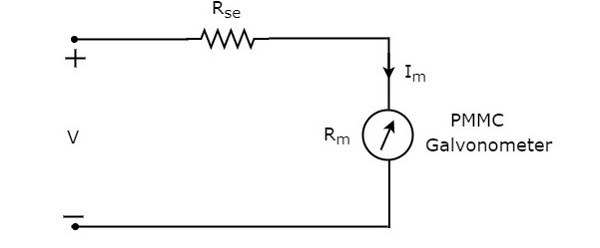
我们必须将此直流电压表置于电路的两个点之间，以测量直流电压。

在上述电路回路中应用**基尔霍夫电压定律(KVL)**。

$V-I_{m}R_{se}-I_{m}R_{m}=0$ (公式1)

$$\Rightarrow V-I_{m}R_{m}=I_{m}R_{se}$$

$$\Rightarrow R_{se}=\frac{V-I_{m}R_{m}}{I_{m}}$$

$\Rightarrow R_{se}=\frac{V}{I_{m}}-R_{m}$ (公式2)

其中，

$R_{se}$是串联倍增电阻

$V$是要测量的直流电压的全量程

$I_{m}$是满刻度偏转电流

$R_{m}$是检流计的内阻

要测量的直流电压的全量程$V$与检流计上的直流电压降$V_{m}$的比率称为**倍增系数**，m。在数学上，它可以表示为

$m=\frac{V}{V_{m}}$ (公式3)

从公式1，我们将得到以下公式，用于计算要测量的直流电压的全量程$V$。

$V=I_{m}R_{se}+I_{m}R_{m}$ (公式4)

检流计上的直流电压降$V_{m}$是满刻度偏转电流$I_{m}$与检流计内阻$R_{m}$的乘积。在数学上，可以写成

$V_{m}=I_{m}R_{m}$ (公式5)

**代入**公式4和公式5到公式3。

$$m=\frac{I_{m}R_{se}+I_{m}R_{m}}{I_{m}R_{m}}$$

$\Rightarrow m=\frac{R_{se}}{R_{m}}+1$

$\Rightarrow m-1=\frac{R_{se}}{R_{m}}$

$R_{se}=R_{m}\left (m-1 \right )$(公式6)

根据可用数据，我们可以使用公式2或公式6找到**串联倍增电阻的值**。

多量程直流电压表

在上一节中，我们讨论了直流电压表，它是通过将倍增电阻与PMMC检流计串联而获得的。此直流电压表可用于测量**特定范围**的直流电压。

如果我们想使用直流电压表测量**多个范围**的直流电压，则必须使用多个并联倍增电阻代替单个倍增电阻，并且整个电阻组合与PMMC检流计串联。多量程直流电压表的**电路图**如下所示。

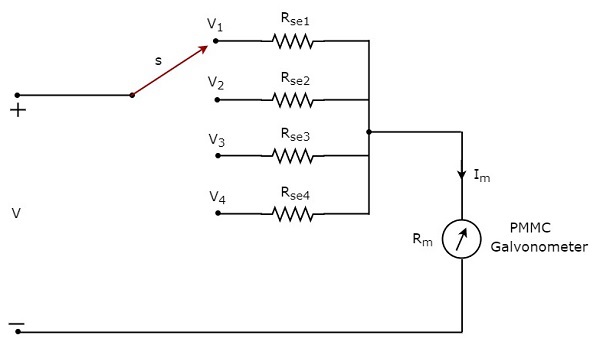
我们必须将此**多量程直流电压表**置于电路的两个点之间，以测量所需范围的直流电压。我们可以通过将开关s连接到相应的倍增电阻来选择所需的电压范围。

设$m_{1},m_{2}, m_{2} $和$m_{4}$分别是当我们将要测量的直流电压的全量程分别考虑为$V_{1} , V_{2}, V_{3}$和$V_{4}$时直流电压表的**倍增系数**。以下是每个倍增系数对应的公式。

$$m_{1}=\frac{V_{1}}{V_{m}}$$

$$m_{2}=\frac{V_{2}}{V_{m}}$$

$$m_{3}=\frac{V_{3}}{V_{m}}$$

$$m_{4}=\frac{V_{4}}{V_{m}}$$

在上图电路中，有四个**串联倍增电阻**，$R_{se1}, R_{se2}, R_{se3}$和$R_{se4}$。以下是与这四个电阻对应的公式。

$$R_{se1}=R_{m}\left (m_{1}-1 \right )$$

$$R_{se2}=R_{m}\left (m_{2}-1 \right )$$

$$R_{se3}=R_{m}\left (m_{3}-1 \right )$$

$$R_{se4}=R_{m}\left (m_{4}-1 \right )$$

因此，我们可以使用上述公式找到每个串联倍增电阻的阻值。

交流电压表

用于测量电路中任意两点之间交流电压的仪器称为**交流电压表**。如果交流电压表包含整流器，则称其为基于整流器的交流电压表。

直流电压表仅测量直流电压。如果我们想用它来测量交流电压，则必须遵循以下两个步骤。

• **步骤1** - 使用整流器将交流电压信号转换为直流电压信号。

• **步骤2** - 测量整流器输出信号的直流或平均值。

我们只需将整流器电路包含到基本的直流电压表中，即可获得**基于整流器的交流电压表**。本章讨论基于整流器的交流电压表。

基于整流器的交流电压表的类型

以下是基于整流器的交流电压表的**两种类型**。

• 使用半波整流器的交流电压表
• 使用全波整流器的交流电压表

现在，让我们逐一讨论这两种交流电压表。

使用半波整流器的交流电压表

如果在直流电压表前面连接一个半波整流器，那么整个组合称为使用半波整流器的交流电压表。使用半波整流器的交流电压表的**方框图**如下所示。

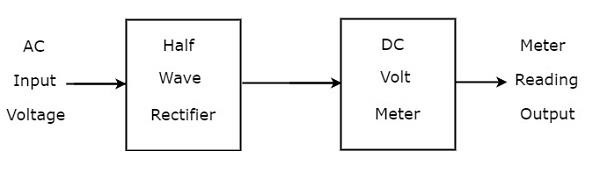
上述方框图包含两个模块：半波整流器和直流电压表。通过用上述方框图中相应的元件替换每个模块，我们可以得到相应的电路图。因此，使用半波整流器的交流电压表的**电路图**如下所示。

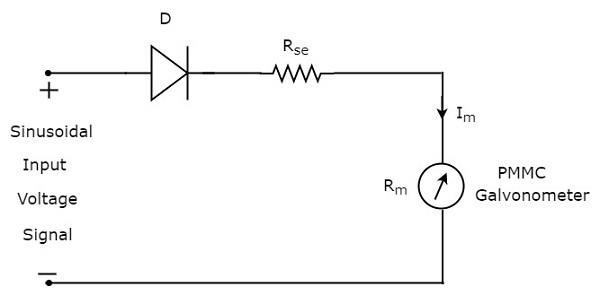
正弦（交流）输入电压信号的**有效值**为

$$V_{rms}=\frac{V_{m}}{\sqrt{2}}$$

$$\Rightarrow V_{m}=\sqrt{2} V_{rms}$$

$$\Rightarrow V_{m}=1.414 V_{rms}$$

其中，

$V_{m}$是正弦（交流）输入电压信号的最大值。

半波整流器输出信号的**直流**或平均值为

$$V_{dc}=\frac{V_{m}}{\pi}$$

**代入**上述公式中的$V_{m}$值。

$$V_{dc}= \frac{1.414 V_{rms}}{\pi}$$

$$V_{dc}= 0.45 V_{rms}$$

因此，交流电压表产生的输出电压等于正弦（交流）输入电压信号有效值的**0.45**倍。

使用全波整流器的交流电压表

如果在直流电压表前面连接一个全波整流器，那么整个组合称为使用全波整流器的交流电压表。使用全波整流器的交流电压表的**方框图**如下所示。

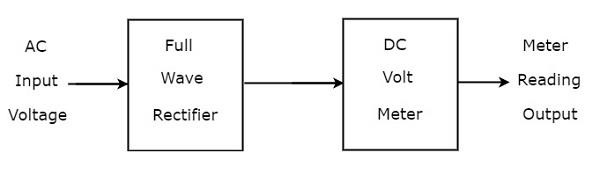
上述方框图包含两个模块：全波整流器和直流电压表。通过用上述方框图中相应的元件替换每个模块，我们可以得到相应的电路图。

因此，使用全波整流器的交流电压表的**电路图**如下所示。

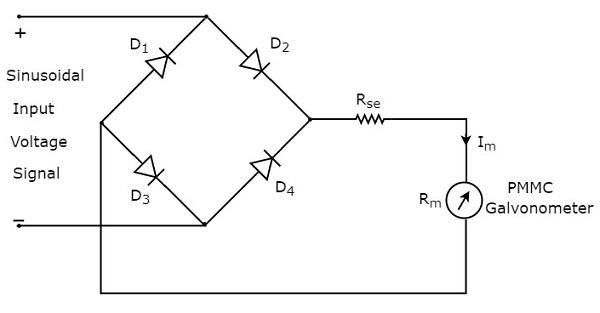
正弦（交流）输入电压信号的**有效值**为

$$V_{rms}=\frac{V_{m}}{\sqrt{2}}$$

$$\Rightarrow V_{m}=\sqrt{2} \:V_{rms}$$

$$\Rightarrow V_{m}= 1.414 V_{rms}$$

其中，

$V_{m}$是正弦（交流）输入电压信号的最大值。

全波整流器输出信号的**直流**或平均值为

$$V_{dc}=\frac{2V_{m}}{\pi}$$

**代入**上述公式中的$V_{m}$值。

$$V_{dc}=\frac{2\times 1.414 \:V_{rms}}{\pi}$$

$$V_{dc}=0.9 \:V_{rms}$$

因此，交流电压表产生的输出电压等于正弦（交流）输入电压信号有效值的**0.9**倍。

其他交流电压表

在上一章中，我们讨论了基于整流器的交流电压表。本章涵盖以下两种类型的交流电压表。

• 峰值响应交流电压表
• 真有效值响应交流电压表

现在，让我们逐一讨论这两种类型的交流电压表。

峰值响应交流电压表

顾名思义，峰值响应交流电压表对交流电压信号的**峰值**做出响应。这意味着，这种电压表测量交流电压的峰值。峰值响应交流电压表的**电路图**如下所示：

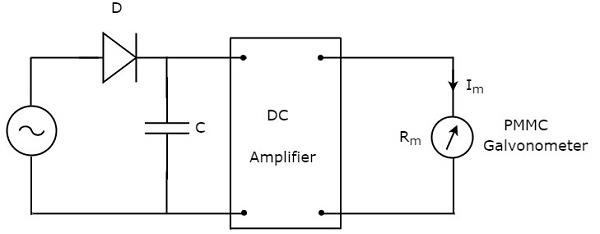
上述电路包括二极管、电容器、直流放大器和PMMC检流计。电路中存在的二极管用于整流目的。因此，二极管将交流电压信号转换为直流电压信号。电容器充电至该直流电压信号的峰值。

在交流电压信号的**正半周期**期间，二极管导通，电容器充电至交流电压信号的峰值。当交流电压信号的值小于此值时，二极管将反向偏置。

因此，电容器将通过直流放大器的电阻放电，直到交流电压信号的下一个正半周期。当交流电压信号的值大于电容器电压时，二极管导通，该过程将重复。

我们应该选择元件值，使电容器快速充电并缓慢放电。结果，仪表始终响应此电容器电压，即**交流电压的峰值**。

真有效值响应交流电压表

顾名思义，真有效值响应交流电压表对交流电压信号的真有效值做出响应。这种电压表测量交流电压的有效值。真有效值响应交流电压表的**电路图**如下所示。

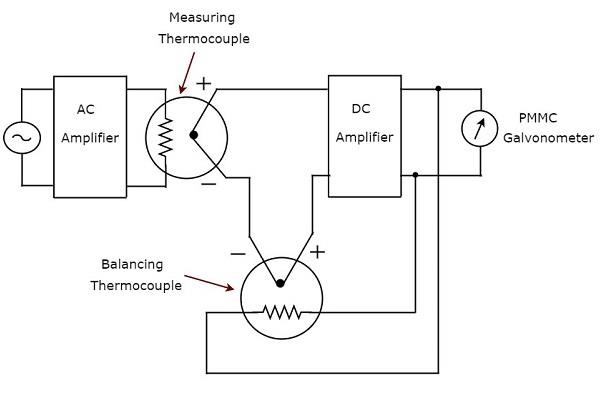
上述电路包括交流放大器、两个热电偶、直流放大器和PMMC检流计。交流放大器放大交流电压信号。上述电路中使用的两个热电偶是测量热电偶和平衡热电偶。**测量热电偶**产生一个输出电压，该电压与交流电压信号的有效值成正比。

任何热电偶都将输入量的平方转换为普通量。这意味着热电偶的输出和输入之间存在非线性关系。通过在反馈电路中使用另一个热电偶，可以忽略热电偶非线性行为的影响。在上述电路中用于此目的的热电偶称为**平衡热电偶**。

两个热电偶，即测量热电偶和平衡热电偶，共同构成直流放大器输入端的桥路。结果，仪表始终响应交流电压信号的**真有效值**。

直流电流表

电流是电荷流动的速率。如果此电荷仅沿一个方向流动，则产生的电流称为直流电（DC）。用于测量直流电的仪器称为**直流电流表**。

如果我们将一个电阻与永磁移动线圈（PMMC）检流计并联，则整个组合充当直流电流表。直流电流表中使用的并联电阻也称为分流电阻或简称为**分流电阻**。为了测量大值的直流电流，此电阻的值应考虑为小值。

直流电流表的**电路图**如下所示。

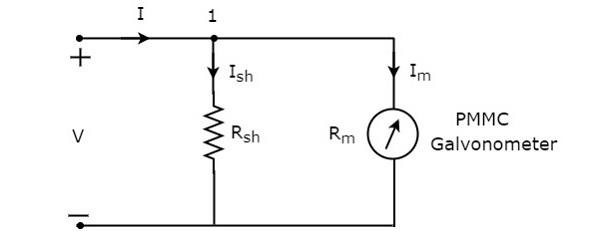
我们必须将此**直流电流表**与电路分支串联，在该分支中要测量直流电流。并联连接的元件上的电压相同。因此，分流电阻$R_{sh}$上的电压和检流计电阻$R_{m}$上的电压相同，因为这两个元件在上述电路中并联连接。**数学上**，可以写成

$$I_{sh}R_{sh}=I_{m}R_{m}$$

$\Rightarrow R_{sh}=\frac{I_{m}R_{m}}{I_{sh}}$ （公式1）

节点1处的**基尔霍夫电流定律方程**为

$$-I+I_{sh}+I_{m}=0$$

$$\Rightarrow I_{sh}=I-I_{m}$$

**代入**公式1中的$I_{sh}$值。

$R_{sh}=\frac{I_{m}R_{m}}{I-I_{m}}$（公式2）

在公式2右侧存在的分子项中，取$I_{m}$作为公因子。

$$R_{sh}=\frac{I_{m}R_{m}}{I_{m}(\frac{1}{I_{m}}-1)}$$

$\Rightarrow R_{sh}=\frac{R_{m}}{\frac{I}{I_{m}}-1}$（公式3）

其中，

$R_{sh}$是分流电阻。

$R_{m}$是检流计的内阻

$I$是要测量的总直流电流。

$I_{m}$是满刻度偏转电流

要测量的总直流电流$I$与检流计的满刻度偏转电流$I_{m}$的比率称为**倍率因子m**。数学上，可以表示为

$m=\frac{I}{I_{m}}$（公式4）

$R_{sh}=\frac{R_{m}}{m-1}$（公式5）

我们可以根据可用数据，使用公式2或公式5找到**分流电阻的值**。

多量程直流电流表

在上一节中，我们讨论了通过将电阻与PMMC检流计并联而获得的直流电流表。此直流电流表可用于测量**特定范围**的直流电流。

如果我们希望使用直流电流表测量**多个范围**的直流电流，则必须使用多个并联电阻代替单个电阻，并且此整个电阻组合与PMMC检流计并联。多量程直流电流表的**电路图**如下所示。

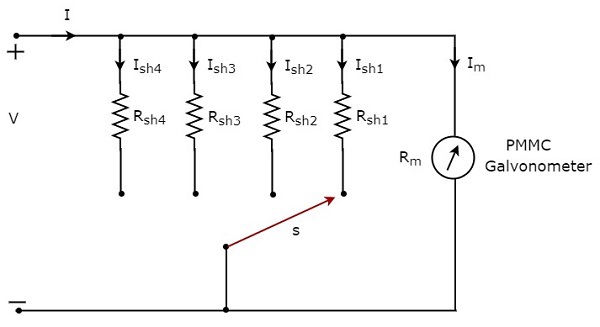
将此多量程直流电流表与电路分支串联，在该分支中要测量所需范围的直流电流。通过将开关s连接到相应的分流电阻，选择所需的电流范围。

假设当我们将要测量的总直流电流分别考虑为$I_{1}、I_{2}、I_{3}$和$I_{4}$时，$m_{1}、m_{2}、m_{3}$和$m_{4}$是直流电流表的**倍率因子**。以下是每个倍率因子对应的公式。

$$m_{1}=\frac{I_{1}}{I_{m}}$$

$$m_{2}=\frac{I_{2}}{I_{m}}$$

$$m_{3}=\frac{I_{3}}{I_{m}}$$

$$m_{4}=\frac{I_{4}}{I_{m}}$$

在上图电路中，有四个**分流电阻**$R_{sh1}、R_{sh2}、R_{sh2}$和$R_{sh4}$。以下是这四个电阻对应的公式。

$$R_{sh1}=\frac{R_{m}}{m_{1}-1}$$

$$R_{sh2}=\frac{R_{m}}{m_{2}-1}$$

$$R_{sh3}=\frac{R_{m}}{m_{3}-1}$$

$$R_{sh4}=\frac{R_{m}}{m_{4}-1}$$

以上公式将帮助我们找到每个分流电阻的阻值。

交流电流表

电流是电荷流动的速率。如果此电荷的方向定期变化，则产生的电流称为**交流电（AC）**。

用于测量流过电路任何分支的交流电流的仪器称为**交流电流表**。

**示例** - 热电偶式交流电流表。

现在，让我们讨论热电偶式交流电流表。

热电偶式交流电流表

如果在PMMC检流计前面连接一个热电偶，则整个组合称为热电偶式交流电流表。热电偶式交流电流表的**方框图**如下所示。

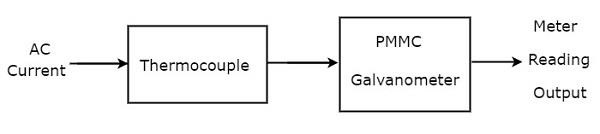
上述方框图主要包含两个模块：热电偶和PMMC检流计。通过用上述方框图中相应的元件替换每个模块，我们可以得到相应的电路图。因此，热电偶式交流电流表的**电路图**如下所示。

当交流电流I流过加热元件时，热电偶会产生电动势e。此电动势e与流过加热元件的电流I的有效值成正比。因此，我们必须校准PMMC仪表的刻度以读取**电流的有效值**。

因此，在本节中，我们完成了所有基本的测量仪器，如直流电压表、交流电压表、直流电流表和交流电流表。在下一章中，让我们讨论测量电阻值的仪表或测量仪器。

欧姆表

用于测量电路中任意两点之间电阻值的仪器称为**欧姆表**。它还可用于查找未知电阻的值。电阻的单位是欧姆，测量仪器是表。因此，“欧姆表”一词是通过组合“欧姆”和“表”两个词而得到的。

欧姆表的类型

以下是欧姆表的**两种类型**。

• 串联欧姆表
• 并联欧姆表

现在，让我们逐一讨论这两种类型的欧姆表。

串联欧姆表

如果电阻的值未知，并且必须通过将其与欧姆表串联来测量，则该欧姆表称为串联欧姆表。串联欧姆表的电路图如下所示。

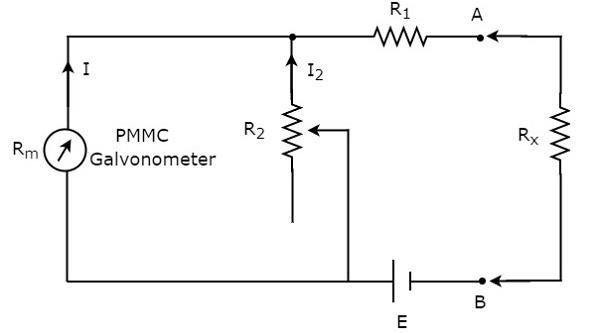
电路中 A & B 端子左侧的部分是串联欧姆表。因此，我们可以通过将其放置在 A & B 端子的右侧来测量未知电阻的值。现在，让我们讨论一下串联欧姆表的刻度尺。

• 如果 $R_{x}= 0 \:\Omega$，则端子 A & B 将彼此短路。因此，电流表电流在电阻 $R_{1}$ 和 $R_{2}$ 之间分配。现在，调整电阻 $R_{2}$ 的值，使整个电流表电流仅流过电阻 $R_{1}$。在这种情况下，电流表显示满刻度偏转电流。因此，电流表的这个满刻度偏转电流可以表示为 $0 \:\Omega$。

• 如果 $R_{x}= \infty \:\Omega$，则端子 A & B 将彼此断路。因此，没有电流流过电阻 $R_{1}$。在这种情况下，电流表显示零偏转电流。因此，电流表的这个零偏转可以表示为 $\infty \Omega$。

• 这样，通过考虑 $R_{x}$ 的不同值，电流表显示不同的偏转。因此，我们可以根据这些偏转对应地表示相应的电阻值。

串联欧姆表包含一个刻度尺。它分别在刻度尺的右手端和左手端标有 0 $\Omega$ 和 $\infty \:\Omega$。串联欧姆表适用于测量高阻值。

并联欧姆表

如果电阻的值未知，并且要通过将其与欧姆表并联（分流）来测量，则该欧姆表称为分流欧姆表。电路图如下所示。

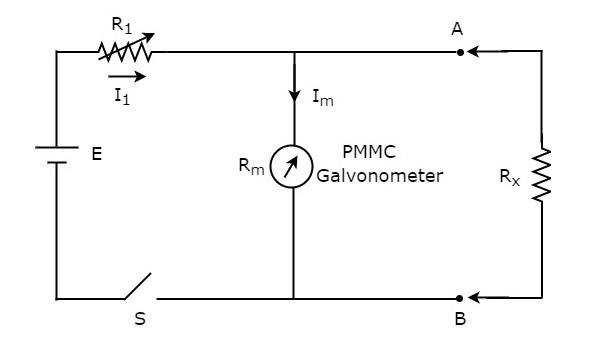
电路中 A & B 端子左侧的部分是分流欧姆表。因此，我们可以通过将其放置在 A & B 端子的右侧来测量未知电阻的值。

现在，让我们讨论一下刻度尺。使用分流欧姆表时，请闭合上述电路的开关 S。

• 如果 $R_{x}=0 \:\Omega$，则端子 A & B 将彼此短路。因此，整个电流 $I_{1}$ 流过端子 A & B。在这种情况下，没有电流流过 PMMC 电流表。因此，PMMC 电流表的零偏转可以表示为 $0 \:\Omega$。

• 如果 $R_{x}=\infty \:\Omega$，则端子 A & B 将彼此断路。因此，没有电流流过端子 A & B。在这种情况下，整个电流 $I_{1}$ 流过 PMMC 电流表。如果需要，调整电阻 $R_{1}$ 的值，直到 PMMC 电流表显示满刻度偏转电流。因此，PMMC 电流表的这个满刻度偏转电流可以表示为 $\infty \:\Omega$

• 这样，通过考虑 $R_{x}$ 的不同值，电流表显示不同的偏转。因此，我们可以根据这些偏转对应地表示相应的电阻值。

分流欧姆表包含一个刻度尺。它分别在刻度尺的左手端和右手端标有 $0 \:\Omega$ 和 $\infty \:\Omega$。

分流欧姆表适用于测量低阻值。因此，我们可以根据要测量的电阻值（即高或低）使用串联欧姆表或分流欧姆表。

万用表

在前面的章节中，我们讨论了电压表、电流表和欧姆表。这些测量仪器分别用于测量电压、电流和电阻。这意味着，我们有单独的测量仪器来测量电压、电流和电阻。

假设，如果可以使用单个测量仪器一次测量电压、电流和电阻等量，则称之为万用表。它被称为万用表，因为它可以一次测量多个电量。

使用万用表进行测量

万用表是一种用于测量直流和交流电压、直流和交流电流以及多个量程的电阻的仪器。它也称为电子万用表或电压欧姆表 (VOM)。

直流电压测量

万用表电路图中可用于测量直流电压的部分如下所示。

上述电路看起来像一个多量程直流电压表。电阻与 PMMC 电流表串联的组合是一个直流电压表。因此，它可以用来测量一定范围内的直流电压。

我们可以通过增加电阻值来增加可以用同一个直流电压表测量的直流电压范围。当我们将电阻串联连接时，等效电阻值会增加。

在上图电路中，我们可以使用电阻 $R_{5}$ 与 PMMC 电流表串联的组合来测量高达2.5V的直流电压。通过将电阻 $R_{4}$ 与之前的电路串联，我们可以测量高达10V的直流电压。这样，我们可以简单地通过将电阻与之前的电路串联来增加直流电压的范围。

我们可以通过将开关 S 连接到所需的电压范围，来测量电路任意两点之间的直流电压。

直流电流测量

万用表电路图中可用于测量直流电流的部分如下所示。

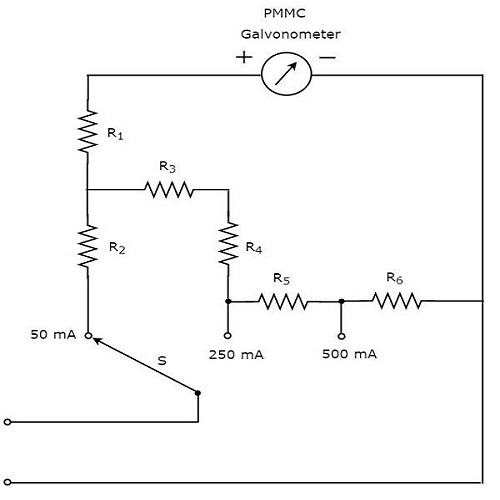
上述电路看起来像一个多量程直流电流表。电阻与 PMMC 电流表并联的组合是一个直流电流表。因此，它可以用来测量一定范围内的直流电流。

我们可以通过将电阻与之前的电阻并联来获得用同一个直流电流表测量的不同量程的直流电流。在上图电路中，电阻 $R_{1}$ 与 PMMC 电流表串联，以防止电流表因过大电流而损坏。

我们可以通过将开关 S 连接到所需的电流范围，来测量流过电路任意两点的直流电流。

交流电压测量

万用表电路图中可用于测量交流电压的部分如下所示。

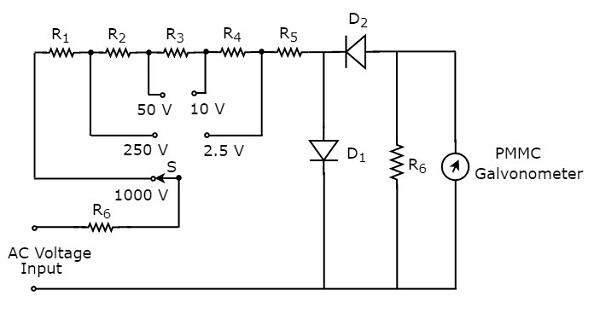
上述电路看起来像一个多量程交流电压表。我们知道，只需将整流器与直流电压表串联（级联）即可得到交流电压表。上述电路只是通过在电阻 $R_{5}$ 和 PMMC 电流表之间放置二极管组合和电阻 $R_{6}$ 而创建的。

我们可以通过将开关 S 连接到所需的电压范围，来测量电路任意两点之间的交流电压。

电阻测量

万用表电路图中可用于测量电阻的部分如下所示。

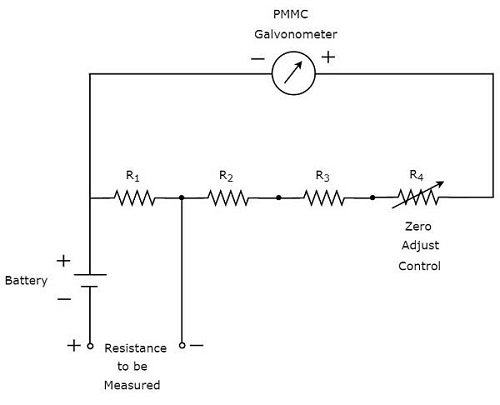
在进行任何测量之前，我们必须执行以下两个任务。

• 短路仪器
• 调整零点调节控制旋钮，直到电流表显示满刻度电流。这意味着电流表指示零电阻值。

现在，上述电路表现为分流欧姆表，并且刻度倍数为 1，即 10⁰。我们还可以将 10 的更高次幂视为刻度倍数，以测量高电阻。

信号发生器

信号发生器是一种电子设备，可提供标准测试信号，如正弦波、方波、三角波等。它也称为振荡器，因为它产生周期性信号。

产生频率在音频频率 (AF) 范围内的周期性信号的信号发生器称为音频信号发生器。音频频率范围为 20Hz 至 20KHz。

音频正弦波和方波发生器

根据需要，在音频频率范围内产生正弦波或方波的音频信号发生器称为音频正弦波和方波发生器。其框图如下所示。

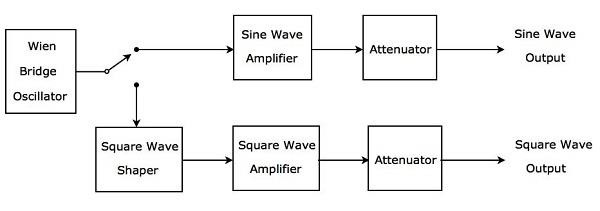
上述框图主要由两条路径组成。它们是上路径和下路径。上路径用于产生音频正弦波，下路径用于产生音频方波。

维恩电桥振荡器将在音频频率范围内产生正弦波。根据需要，我们可以通过开关将维恩电桥振荡器的输出连接到上路径或下路径。

上路径包含正弦波放大器和衰减器等模块。如果使用开关将维恩电桥振荡器的输出连接到上路径，它将在上路径的输出端产生所需的音频正弦波。

下路径包含以下模块：方波整形器、方波放大器和衰减器。方波整形器将正弦波转换为方波。如果使用开关将维恩电桥振荡器的输出连接到下路径，则它将在下路径的输出端产生所需的音频方波。这样，我们考虑的框图可以根据需要产生音频正弦波或音频方波。

函数发生器

函数发生器是一种信号发生器，它产生三种或多种周期波。考虑以下框图，它将产生三角波、方波和正弦波等周期波。

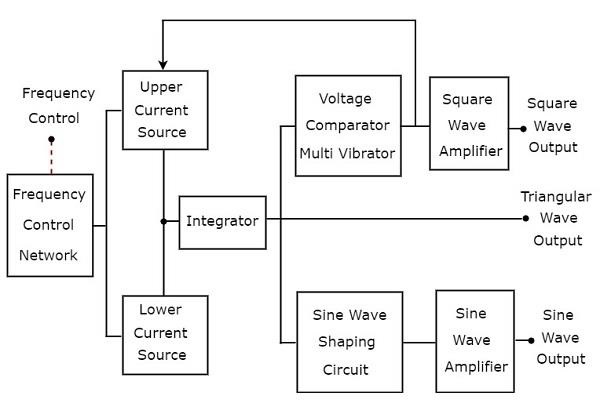
在上图框图中，有两个电流源，即上电流源和下电流源。这两个电流源受频率控制电压调节。

三角波

上图框图中的积分器交替地从上电流源和下电流源获取恒定电流，持续时间相等且重复。因此，积分器将重复产生两种类型的输出，持续时间相同：

• 积分器的输出电压线性增加，相对于积分器从上电流源获取电流期间的时间。

• 积分器的输出电压线性下降，相对于积分器从下电流源获取电流期间的时间。

这样，上图框图中的积分器将产生一个三角波。

方波和正弦波

为了分别获得方波和正弦波，将积分器的输出（即三角波）作为输入应用于上图框图中所示的其他两个模块。让我们逐一讨论这两个模块。

方波

三角波具有正斜率和负斜率，交替出现，持续时间相等且重复。因此，上图框图中的电压比较器多谐振荡器将产生以下两种类型的输出，持续时间相等且重复：

• 在电压比较器多谐振荡器获取三角波正斜率期间，电压比较器多谐振荡器输出端的一种恒定（较高）电压。

• 另一种类型的恒定（较低）电压出现在电压比较器多谐振荡器的输出端，该电压比较器多谐振荡器在此期间获得三角波的负斜率。

上述框图中存在的电压比较器多谐振荡器将产生方波。如果在电压比较器多谐振荡器输出端产生的方波的幅度不足，则可以使用方波放大器将其放大到所需的值。

正弦波

正弦波整形电路将从三角形输入波产生正弦波输出。基本上，该电路由二极管电阻网络组成。如果在正弦波整形电路输出端产生的正弦波的幅度不足，则可以使用正弦波放大器将其放大到所需的值。

波形分析仪

用于分析波形的电子仪器称为波形分析仪。它也称为信号分析仪，因为信号和波形这两个术语可以经常互换使用。

我们可以将周期信号表示为以下两个项的和。

• 直流分量
• 一系列正弦谐波

因此，周期信号的分析就是其中存在的谐波分量的分析。

基本波形分析仪

基本波形分析仪主要由三个模块组成：初级检测器、全波整流器和PMMC电流计。下图显示了基本波形分析仪的框图：

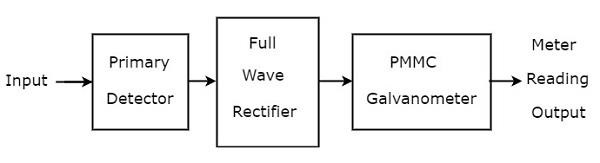
下面提到了基本波形分析仪中每个模块的功能。

• 初级检测器 - 它由一个LC电路组成。我们可以调整电感L和电容C的值，使其仅允许待测量的所需谐波频率分量通过。

• 全波整流器 - 它将交流输入转换为直流输出。

• PMMC电流计 - 它显示信号的峰值，该峰值在全波整流器的输出端获得。

通过将基本波形分析仪上述框图中的每个模块替换为相应的组件，我们将得到相应的电路图。因此，基本波形分析仪的电路图将如下图所示：

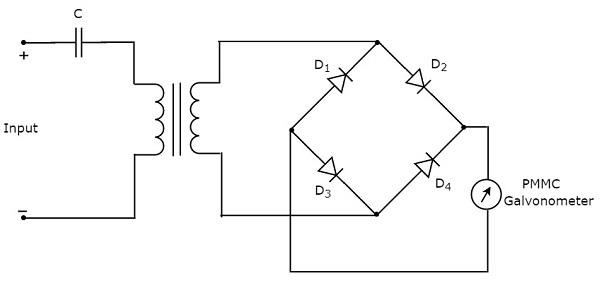
此基本波形分析仪可用于分析周期信号的每个谐波频率分量。

波形分析仪的类型

波形分析仪可以分为以下两种类型。

• 频率选择性波形分析仪
• 超外差波形分析仪

现在，让我们逐一讨论这两种波形分析仪。

频率选择性波形分析仪

用于分析音频范围信号的波形分析仪称为频率选择性波形分析仪。下图显示了频率选择性波形分析仪的框图。

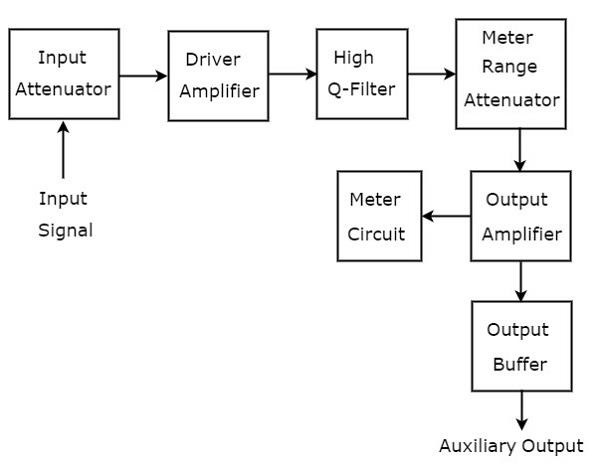
频率选择性波形分析仪由一组模块组成。下面提到了每个模块的功能。

• 输入衰减器 - 待分析的音频信号应用于输入衰减器。如果信号幅度过大，则可以通过输入衰减器进行衰减。

• 驱动放大器 - 在必要时放大接收到的信号。

• 高Q滤波器 - 用于选择所需频率并抑制不需要的频率。它由两个RC部分和两个滤波放大器组成，所有这些都级联在一起。我们可以改变电容值以将频率范围改变10的幂次。类似地，我们可以改变电阻值以在选定的范围内改变频率。

• 仪表范围衰减器 - 它将选定的音频信号作为输入，并在需要时产生衰减输出。

• 输出放大器 - 在必要时放大选定的音频信号。

• 输出缓冲器 - 用于将选定的音频信号提供给输出设备。

• 仪表电路 - 显示选定音频信号的读数。我们可以选择伏特范围或分贝范围的仪表读数。

超外差波形分析仪

用于分析射频范围信号的波形分析仪称为超外差波形分析仪。下图显示了超外差波形分析仪的框图。

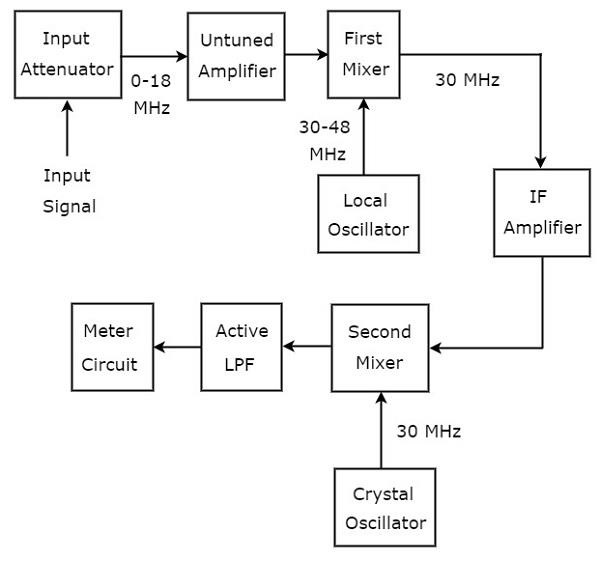
下面提到了超外差波形分析仪的工作原理。

• 待分析的射频信号应用于输入衰减器。如果信号幅度过大，则可以通过输入衰减器进行衰减。

• 无调放大器在必要时放大射频信号，并将其应用于第一混频器。

• 射频信号和本地振荡器输出的频率范围分别为0-18 MHz和30-48 MHz。因此，第一混频器产生一个输出，其频率为30 MHz。这是应用于它的两个信号频率的差值。

• 中频放大器放大中频（IF）信号，即第一混频器的输出。放大的中频信号应用于第二混频器。

• 放大后的中频信号和晶体振荡器输出的频率相同，均为30MHz。因此，第二混频器产生一个输出，其频率为0 Hz。这是应用于它的两个信号频率的差值。

• 有源低通滤波器（LPF）的截止频率选择为1500 Hz。因此，此滤波器允许通过第二混频器的输出信号。

• 仪表电路显示射频信号的读数。我们可以选择伏特范围或分贝范围的仪表读数。

因此，我们可以根据待分析信号的频率范围选择特定的波形分析仪。

频谱分析仪

用于在频域分析波形的电子仪器称为频谱分析仪。基本上，它在其CRT屏幕上显示信号的能量分布。这里，x轴表示频率，y轴表示幅度。

频谱分析仪的类型

我们可以将频谱分析仪分为以下两种类型。

• 滤波器组频谱分析仪
• 超外差频谱分析仪

现在，让我们逐一讨论这两种频谱分析仪。

滤波器组频谱分析仪

用于分析音频范围信号的频谱分析仪称为滤波器组频谱分析仪，或实时频谱分析仪，因为它显示（显示）所有输入频率的任何变化。

下图显示了滤波器组频谱分析仪的框图。

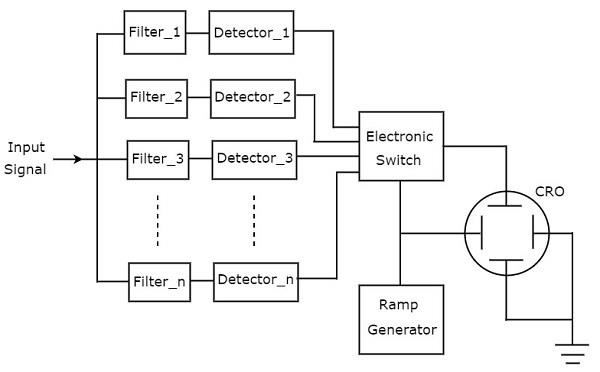
下面提到了滤波器组频谱分析仪的工作原理。

• 它有一组带通滤波器，每个滤波器都设计用于允许特定频段的频率通过。每个带通滤波器的输出都提供给相应的检测器。

• 所有检测器输出都连接到电子开关。该开关允许检测器输出依次连接到示波器的垂直偏转板。因此，示波器在其CRT屏幕上显示音频信号的频率频谱。

超外差频谱分析仪

用于分析射频范围信号的频谱分析仪称为超外差频谱分析仪。其框图如下所示。

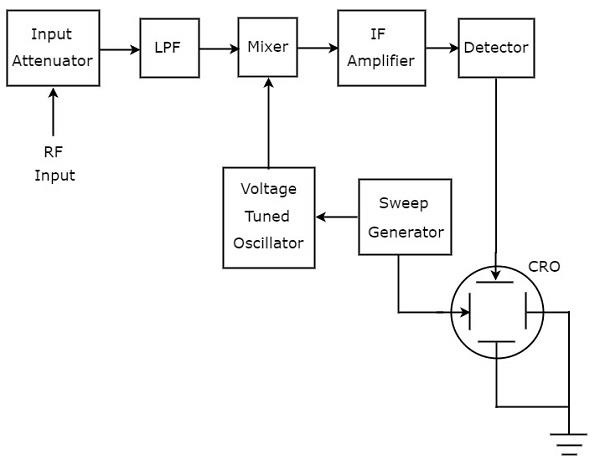
下面提到了超外差频谱分析仪的工作原理。

• 待分析的射频信号应用于输入衰减器。如果信号幅度过大，则可以通过输入衰减器进行衰减。

• 低通滤波器（LPF）仅允许频率低于截止频率的分量通过。

• 混频器接收来自低通滤波器和电压调谐振荡器的输入。它产生一个输出，该输出是应用于它的两个信号频率的差值。

• 中频放大器放大中频（IF）信号，即混频器的输出。放大的中频信号应用于检测器。

检测器的输出提供给示波器的垂直偏转板。因此，示波器在其CRT屏幕上显示射频信号的频率频谱。

因此，我们可以根据待分析信号的频率范围选择特定的频谱分析仪。

示波器的基础

示波器是一种电子设备，用于显示电压波形。在示波器中，阴极射线示波器（CRO）是最基本的，它显示随时间变化的信号或波形。

在本章中，我们将讨论CRO的框图以及使用CRO测量某些参数。

CRO的框图

阴极射线示波器（CRO）由一组模块组成。分别是垂直放大器、延迟线、触发电路、时基发生器、水平放大器、阴极射线管（CRT）和电源。下图显示了CRO的框图。

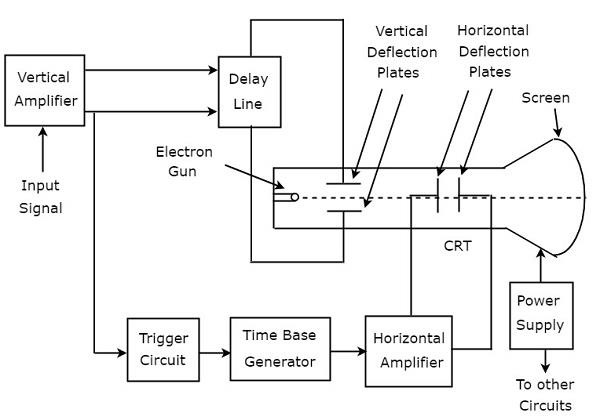
下面提到了CRO每个模块的功能。

• 垂直放大器 - 放大待在CRT屏幕上显示的输入信号。

• 延迟线 - 为在垂直放大器输出端获得的信号提供一定量的延迟。然后将此延迟信号应用于CRT的垂直偏转板。

• 触发电路 - 生成触发信号以同步电子束的水平和垂直偏转。

• 时基发生器 - 生成锯齿波信号，该信号用于电子束的水平偏转。

• 水平放大器 - 放大锯齿波信号，然后将其连接到CRT的水平偏转板。

• 电源 - 生成高电压和低电压。负高电压和正低电压分别应用于CRT和其他电路。

• 阴极射线管（CRT） - 是CRO中最重要的模块，主要由四个部分组成。分别是电子枪、垂直偏转板、水平偏转板和荧光屏。

电子枪产生的电子束分别被一对垂直偏转板和一对水平偏转板在垂直和水平方向上偏转。最后，偏转的光束将作为荧光屏上的一个亮点出现。

这样，CRO将在CRT屏幕上显示所施加的输入信号。因此，我们可以使用CRO在时域中分析信号

使用CRO进行测量

我们可以使用CRO进行以下测量。

• 幅度测量
• 周期测量
• 频率测量

现在，让我们逐一讨论这些测量。

幅度测量

CRO在其屏幕上显示电压信号作为时间的函数。该电压信号的幅度是恒定的，但我们可以通过改变CRO面板上的伏特/格旋钮来改变垂直方向上覆盖电压信号的格数。因此，我们将使用以下公式获得出现在CRO屏幕上的信号的幅度。

$$A=j\times n_{v}$$

其中，

$A$是幅度

$j$是伏特/格的值

$n_{v}$是垂直方向上覆盖信号的格数。

周期测量

CRO在其屏幕上显示电压信号作为时间的函数。该周期性电压信号的周期是恒定的，但我们可以通过改变CRO面板上的时间/格旋钮来改变水平方向上覆盖电压信号一个完整周期的格数。

因此，我们将使用以下公式获得出现在CRO屏幕上的信号的周期。

$$T=k\times n_{h}$$

其中，

$T$是周期

$j$是时间/格的值

$n_{v}$是水平方向上覆盖周期信号一个完整周期的格数。

频率测量

周期信号的频率f是周期的倒数T。数学上，它可以表示为

$$f=\frac{1}{T}$$

因此，我们可以通过以下两个步骤找到周期信号的频率f。

• 步骤1 - 查找周期信号的周期

• 步骤2 - 取步骤1中获得的周期信号倒数

我们将在下一章讨论专用示波器。

专用示波器

在上一章中，我们讨论了阴极射线示波器（CRO），它是一种基本示波器。根据需要，只需在基本示波器上增加几个附加模块，就可以得到专用示波器。

以下是专用示波器。

• 双束示波器
• 双迹示波器
• 数字存储示波器

现在，让我们逐一讨论这些专用示波器。

双束示波器

显示两个电压波形的示波器称为双束示波器。其框图如下所示。

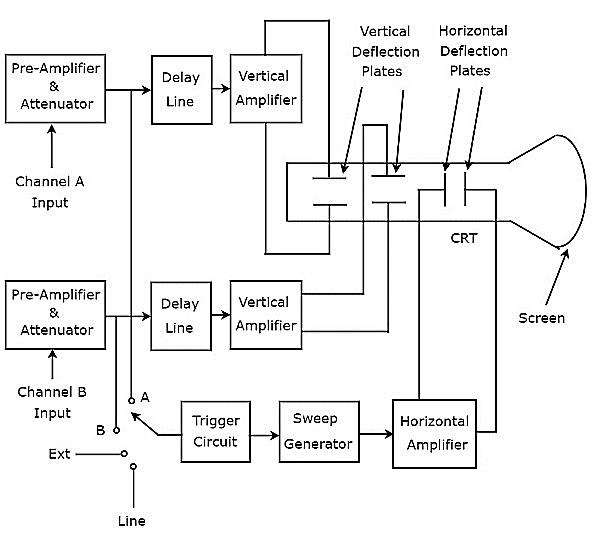
如上图所示，双束示波器的CRT由两组垂直偏转板和一组水平偏转板组成。

以下模块组合在一起称为通道。

• 前置放大器和衰减器
• 延迟线
• 垂直放大器
• 一组垂直偏转板

双束示波器有两个通道。因此，我们可以将两个信号（即A和B）分别作为通道A和通道B的输入。我们可以使用开关选择这四个信号中的任意一个作为触发输入到触发电路。这些是输入信号A和B、外部信号（Ext）和线路输入。

由于有两对垂直偏转板，因此该示波器将产生两束垂直偏转的光束。在这个示波器中，用于水平方向偏转光束的模块对两个输入信号都是通用的。最后，该示波器将在CRT屏幕上同时显示两个输入信号。

双迹示波器

在屏幕上产生两条轨迹的示波器称为双迹示波器。其框图如下所示。

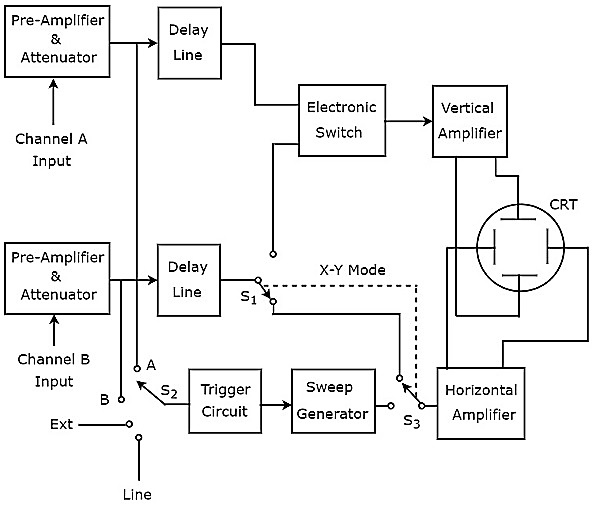
如上图所示，双迹示波器的CRT由一组垂直偏转板和另一组水平偏转板组成。通道由四个模块组成，即前置放大器和衰减器、延迟线、垂直放大器和垂直偏转板。

在上图框图中，前两个模块在两个通道中分别存在。最后两个模块对两个通道都是通用的。因此，借助电子开关，我们可以将特定通道的延迟线输出连接到垂直放大器。

我们可以使用开关选择这四个信号中的任意一个作为触发电路的触发输入。这些是输入信号A和B、外部信号（Ext）和线路输入。

该示波器使用相同的电子束通过电子开关在垂直方向上偏转输入信号A和B，并产生两条轨迹。水平偏转光束的模块对两个输入信号都是通用的。

数字存储示波器

以数字方式存储波形的示波器称为数字存储示波器。数字存储示波器的框图如下所示。

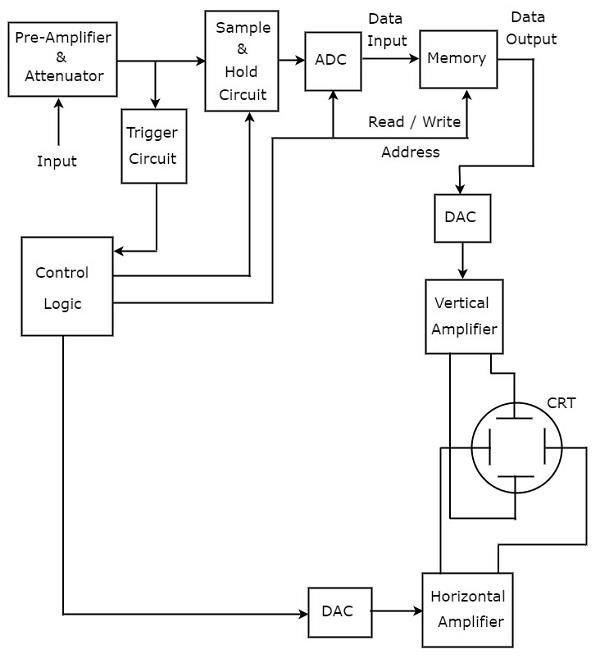
为了将基本示波器转换为数字存储示波器，需要添加用于数字数据存储的附加模块。用于存储数字数据的模块位于数字存储示波器中的前置放大器和衰减器以及垂直放大器之间。这些是采样保持电路、模数转换器（ADC）、存储器和数模转换器。

控制逻辑通过发送各种控制信号来控制前三个模块。控制逻辑和数模转换器等模块存在于数字存储示波器中的触发电路和水平放大器之间。

数字存储示波器在屏幕上显示波形之前存储数据为数字形式。而基本示波器没有此功能。

李萨如图形

利萨如图形是在将正弦信号施加到CRO的水平和垂直偏转板时显示在屏幕上的图案。这些图案将根据施加到CRO的水平和垂直偏转板的正弦信号的幅度、频率和相位差而变化。

下图显示了示例利萨如图形。

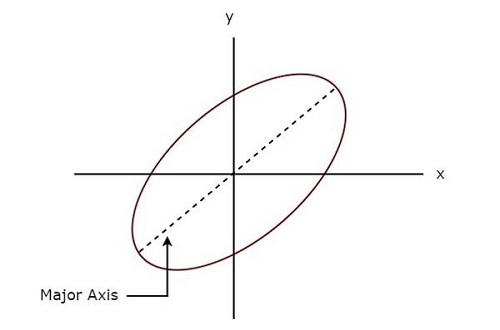
上述利萨如图形为椭圆形，其长轴与正x轴有一定的倾斜角。

使用利萨如图形进行测量

我们可以从利萨如图形中进行以下两种测量。

• 正弦信号的频率
• 两个正弦信号之间的相位差

现在，让我们逐一讨论这两种测量方法。

频率测量

当将正弦信号施加到CRO的水平和垂直偏转板时，利萨如图形将显示在屏幕上。因此，将具有标准已知频率的正弦信号施加到CRO的水平偏转板。同样，将频率未知的正弦信号施加到CRO的垂直偏转板。

设$f_{H}$和$f_{V}$分别为施加到CRO的水平和垂直偏转板的正弦信号的频率。$f_{H}$和$f_{V}$之间的关系可以用数学表示如下。

$$\frac{f_{V}}{f_{H}}=\frac{n_{H}}{n_{V}}$$

从上述关系，我们将得到施加到CRO的垂直偏转板的正弦信号的频率为

$f_{V}=\left ( \frac{n_{H}}{n_{V}} \right )f_{H}$（公式1）

其中，

$n_{H}$是水平切线的数量

$n_{V}$是垂直切线的数量

我们可以从利萨如图形中找到$n_{H}$和$n_{V}$的值。因此，将$n_{H}$、$n_{V}$和$f_{H}$的值代入公式1，我们将得到$f_{V}$的值，即施加到CRO的垂直偏转板的正弦信号的频率。

相位差测量

当将正弦信号施加到CRO的水平和垂直偏转板时，利萨如图形将显示在屏幕上。因此，将具有相同幅度和频率的正弦信号施加到CRO的水平和垂直偏转板。

对于一些基于其形状的利萨如图形，我们可以直接说出两个正弦信号之间的相位差。

• 如果利萨如图形是与正x轴成$45^{\circ}$角的直线，则两个正弦信号之间的相位差为$0^{\circ}$。这意味着这两个正弦信号之间没有相位差。

• 如果利萨如图形是与正x轴成$135^{\circ}$角的直线，则两个正弦信号之间的相位差为$180^{\circ}$。这意味着这两个正弦信号反相。

• 如果利萨如图形为圆形，则两个正弦信号之间的相位差为$90^{\circ}$或$270^{\circ}$。

当利萨如图形为椭圆形时，我们可以使用公式计算两个正弦信号之间的相位差。

• 如果椭圆形利萨如图形的长轴与正x轴的倾斜角在$0^{\circ}$到$90^{\circ}$之间，则两个正弦信号之间的相位差为。

$$\phi =\sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=\sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$

• 如果椭圆形利萨如图形的长轴与正x轴的倾斜角在$90^{\circ}$到$180^{\circ}$之间，则两个正弦信号之间的相位差为。

$$\phi =180 - \sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=180 - \sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$

其中，

$x_{1}$是原点到x轴上椭圆形利萨如图形相交点的距离

$x_{2}$是原点到椭圆形利萨如图形垂直切线的距离

$y_{1}$是原点到y轴上椭圆形利萨如图形相交点的距离

$y_{2}$是原点到椭圆形利萨如图形水平切线的距离

在本章中，我们学习了如何使用公式从利萨如图形中找到未知正弦信号的频率以及两个正弦信号之间的相位差。

示波器探头

我们可以通过探头将任何测试电路连接到示波器。由于CRO是基本示波器，因此连接到它的探头也称为CRO探头。

我们应该选择探头，使其不会对测试电路造成任何负载问题。这样我们就可以在CRO屏幕上正确地分析测试电路的信号。

CRO探头应具有以下特性。

• 高阻抗
• 高带宽

CRO探头的框图如下所示。

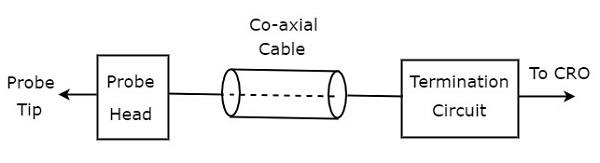
如图所示，CRO探头主要由三个模块组成。这些是探头头、同轴电缆和终端电路。同轴电缆只是连接探头头和终端电路。

CRO探头的类型

CRO探头可以分为以下两种类型。

• 无源探头
• 有源探头

现在，让我们逐一讨论这两种类型的探头。

无源探头

如果探头头由无源元件组成，则称为无源探头。无源探头的电路图如下所示。

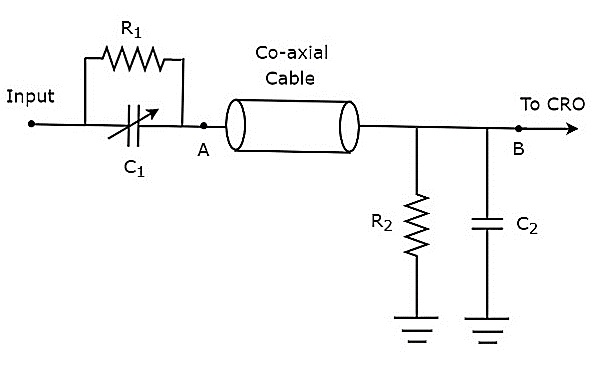
如图所示，探头头由电阻$R_{1}$和可变电容器$C_{1}$的并联组合组成。类似地，终端电路由电阻$R_{2}$和电容器$C_{2}$的并联组合组成。

上述电路图以桥式电路的形式修改，如下所示。

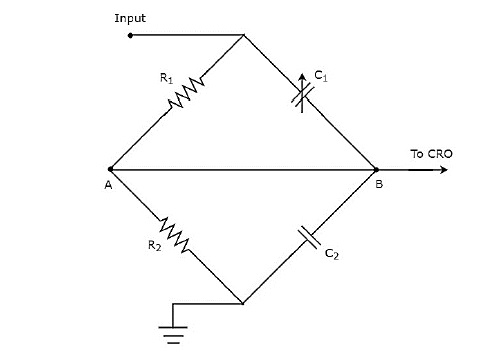
我们可以通过调整可变电容器$c_{1}$的值来平衡桥路。我们将在后面的章节中讨论桥路的概念。目前，请考虑以下交流桥的平衡条件。

$$Z_{1}Z_{4}=Z_{2}Z_{3}$$

代入阻抗$Z_{1}、Z_{2}、Z_{3}$和$Z_{4}$分别为$R_{1}、\frac{1}{j\omega C_{1}}、R_{2}$和$\frac{1}{j\omega C_{2}}$到上式中。

$$R_{1}\left ( \frac{1}{j \omega C_{2}} \right )=\left ( \frac{1}{j \omega C_{1}} \right )R_{2}$$

$\Rightarrow R_{1} C_{1}=R_{2} C_{2}$公式 1

根据分压原理，我们可以得到**电阻R₂两端的电压**为

$$V_{0}=V_{i}\left ( \frac{R_{2}}{R_{1}+R_{2}} \right )$$

**衰减因子**是输入电压V_i和输出电压V₀的比值。因此，从上式我们可以得到衰减因子α为

$$\alpha = \frac{V_{i}}{V_{0}}=\frac{R_{1}+R_{2}}{R_{2}}$$

$\Rightarrow \alpha = 1+\frac{R_{1}}{R_{2}}$

$\Rightarrow \alpha-1 = \frac{R_{1}}{R_{2}}$

$\Rightarrow R_{1}= \left ( \alpha-1 \right )R_{2}$公式 2

从公式 2，我们可以得出结论，对于α > 1的整数，R₁的值大于或等于R₂的值。

将公式 2 代入公式 1。

$$\left ( \alpha-1 \right )R_{2}C_{1}=R_{2}C_{2}$$

$\Rightarrow \left ( \alpha-1 \right )C_{1} =C_{2}$

$\Rightarrow C_{1}=\frac{C_{2}}{\left ( \alpha-1 \right )}$公式 3

从公式 3，我们可以得出结论，对于α > 1的整数，C₁的值小于或等于C₂的值。

示例

让我们找到一个衰减因子α为 10 的探头的R₁和C₁的值。假设R₂=1 MΩ，C₂=18pF。

• **步骤 1** - 我们将通过将α和R₂的值代入公式 2 来得到R₁的值。

$$ R_{1}=\left ( 10-1 \right )\times 1 \times 10^{6}$$

$$\Rightarrow R_{1}=9 \times 10^{6}$$

$$\Rightarrow R_{1}=9 M\Omega$$

**步骤 2** - 我们将通过将α和C₂的值代入公式 3 来得到C₁的值。

$$C_{1}=\frac{18\times10^{-12}}{\left ( 10-1 \right )}$$

$$\Rightarrow C_{1}=2 \times 10^{-12}$$

$$\Rightarrow C_{1}=2 pF$$

因此，对于给定的规格，探头的R₁和C₁的值将分别为9MΩ和2pF。

有源探头

如果探头头部包含有源电子元件，则称为**有源探头**。有源探头的框图如下所示。

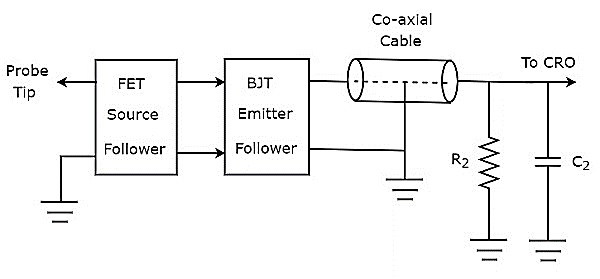
如图所示，探头头部包含一个FET源跟随器级联一个BJT发射极跟随器。FET源跟随器提供高输入阻抗和低输出阻抗。而BJT发射极跟随器的目的是避免或消除阻抗失配。

其他两个部分，如同轴电缆和终端电路，在有源探头和无源探头中保持相同。

电子测量仪器 - 电桥

如果电气元件以桥或环形结构的形式排列，则该电路称为**电桥**。一般来说，电桥形成一个具有四臂或四支路的回路。每个支路可能包含一个或两个电气元件。

电桥的类型

我们可以根据这些电桥可以工作的电压信号，将电桥电路或电桥分为以下两类。

• 直流电桥
• 交流电桥

现在，让我们简要讨论一下这两种电桥。

直流电桥

如果电桥电路只能用直流电压信号工作，则它就是直流电桥电路或简称**直流电桥**。直流电桥用于测量未知电阻的值。直流电桥的**电路图**如下所示。

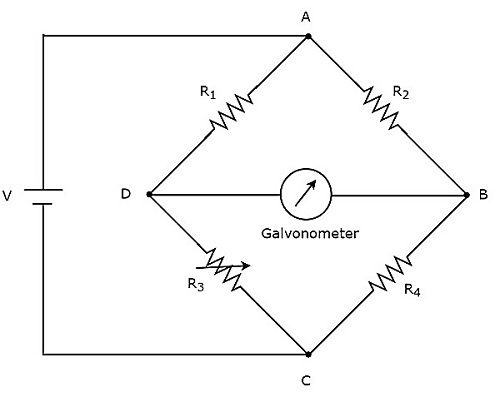
上述直流电桥有**四臂**，每臂都包含一个电阻。其中，两个电阻具有固定的电阻值，一个电阻是可变电阻，另一个具有未知的电阻值。

上述直流电桥电路可以通过放置在一个对角线上**直流电源**来激励。检流计放置在直流电桥的另一个对角线上。只要电桥不平衡，它就会显示一些偏转。

改变可变电阻的阻值，直到检流计显示零偏转。现在，上述直流电桥被称为平衡电桥。因此，我们可以使用节点方程找到**未知电阻**的值。

交流电桥

如果电桥电路只能用交流电压信号工作，则称其为交流电桥电路或简称**交流电桥**。交流电桥用于测量未知电感、电容和频率的值。

交流电桥的**电路图**如下所示。

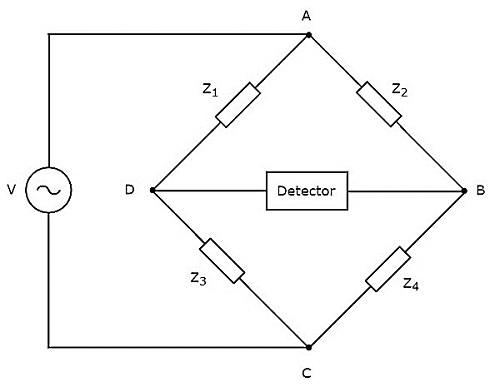
交流电桥的电路图类似于直流电桥。上述交流电桥有**四臂**，每臂都包含一些阻抗。这意味着，每臂将包含单个或组合的无源元件，例如电阻、电感和电容。

在四个阻抗中，两个阻抗具有固定值，一个阻抗是可变的，另一个是未知的阻抗。

上述交流电桥电路可以通过放置在一个对角线上**交流电源**来激励。一个检测器放置在交流电桥的另一个对角线上。只要电桥不平衡，它就会显示一些偏转。

上述交流电桥电路可以通过放置在一个对角线上**交流电源**来激励。一个检测器放置在交流电桥的另一个对角线上。只要电桥不平衡，它就会显示一些偏转。

改变可变阻抗的阻抗值，直到检测器显示零偏转。现在，上述交流电桥被称为平衡电桥。因此，我们可以使用平衡条件找到**未知阻抗**的值。

直流电桥

**直流电桥**只能用直流电压信号工作。直流电桥可用于测量存在于电桥中的未知电阻的值。惠斯通电桥是直流电桥的一个例子。

现在，让我们讨论**惠斯通电桥**，以便找到未知电阻的值。

惠斯通电桥

惠斯通电桥是一种简单的直流电桥，主要有四臂。这四臂形成菱形或正方形，每臂包含一个电阻。

要找到未知电阻的值，我们需要检流计和直流电压源。因此，这两个中的一个放置在惠斯通电桥的一个对角线上，另一个放置在惠斯通电桥的另一个对角线上。

惠斯通电桥用于测量中等电阻的值。惠斯通电桥的**电路图**如下所示。

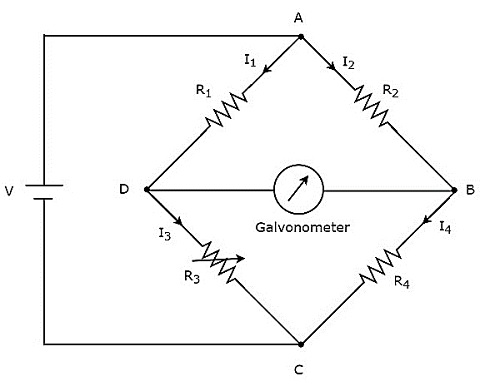
在上图电路中，AB、BC、CD和DA臂共同形成一个**菱形**或正方形。它们分别包含电阻R₂、R₄、R₃和R₁。设流过这些电阻臂的电流分别为I₂、I₄、I₃和I₁，这些电流的方向如图所示。

对角线DB和AC分别包含检流计和V伏的直流电压源。这里，电阻R₃是标准的可变电阻，电阻R₄是未知电阻。我们可以通过改变电阻R₃的阻值来**平衡电桥**。

当没有电流流过对角线臂DB时，上述电桥电路处于平衡状态。这意味着，当电桥平衡时，检流计**没有偏转**。

当满足以下**两个条件**时，电桥将处于平衡状态。

• AD臂上的电压等于AB臂上的电压。即，

$$V_{AD}=V_{AB}$$

$\Rightarrow I_{1}R_{1}=I_{2}R_{2}$公式 1

• DC臂上的电压等于BC臂上的电压。即，

$$V_{DC}=V_{BC}$$

$\Rightarrow I_{3}R_{3}=I_{4}R_{4}$公式 2

从上述两个平衡条件，我们将得到以下**两个结论**。

• 流过AD臂的电流将等于DC臂的电流。即，

$$I_{1}=I_{3}$$

• 流过AB臂的电流将等于BC臂的电流。即，

$$I_{2}=I_{4}$$

取公式 1 和公式 2 的比值。

$\frac{I_{1}R_{1}}{I_{3}R_{3}}=\frac{I_{2}R_{2}}{I_{4}R_{4}}$公式 3

将I₁=I₃和I₂=I₄代入公式 3。

$$\frac{I_{3}R_{1}}{I_{3}R_{3}}=\frac{I_{4}R_{2}}{I_{4}R_{4}}$$

$$\Rightarrow \frac{R_{1}}{R_{3}}=\frac{R_{2}}{R_{4}}$$

$$\Rightarrow R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$

通过将电阻R₁、R₂和R₃的已知值代入上式，我们将得到**电阻R₄的值**。

交流电桥

在本章中，让我们讨论一下可用于测量电感的交流电桥。交流电桥仅用交流电压信号工作。交流电桥的**电路图**如下所示。

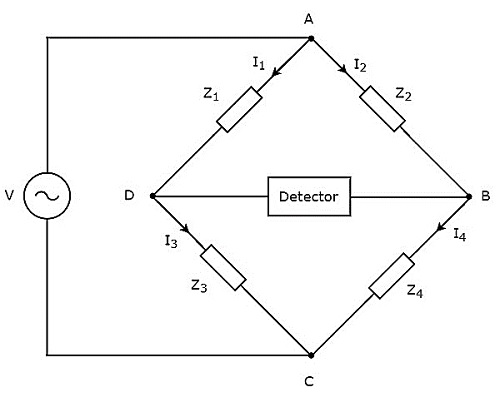
如上图所示，交流电桥主要由四臂组成，它们以菱形或**正方形**连接。所有这些臂都包含一些阻抗。

为了找到未知阻抗的值，还需要检测器和交流电压源。因此，这两个中的一个放置在交流电桥的一个对角线上，另一个放置在交流电桥的另一个对角线上。惠斯通电桥的平衡条件为 -

$$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$

我们将得到**交流电桥的平衡条件**，只需将上式中的R替换为Z即可。

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$\Rightarrow Z_{1}Z_{4}=Z_{2}Z_{3}$

这里，Z₁和Z₂是固定阻抗。而Z₃是标准的可变阻抗，Z₄是未知阻抗。

**注意** - 我们可以根据应用选择这四个阻抗中的任意两个作为固定阻抗，一个阻抗作为标准可变阻抗，另一个阻抗作为未知阻抗。

以下两个交流电桥可用于测量**电感**。

• 麦克斯韦电桥
• 海电桥

现在，让我们逐一讨论一下这两种交流电桥。

麦克斯韦电桥

麦克斯韦电桥是一种具有四臂的交流电桥，它们以菱形或**正方形**的形式连接。该电桥的两臂包含单个电阻，一臂包含电阻和电感的串联组合，另一臂包含电阻和电容的并联组合。

交流检测器和交流电压源用于找到未知阻抗的值。因此，这两个中的一个放置在麦克斯韦电桥的一个对角线上，另一个放置在麦克斯韦电桥的另一个对角线上。

麦克斯韦电桥用于测量中等电感的值。麦克斯韦电桥的**电路图**如下所示。

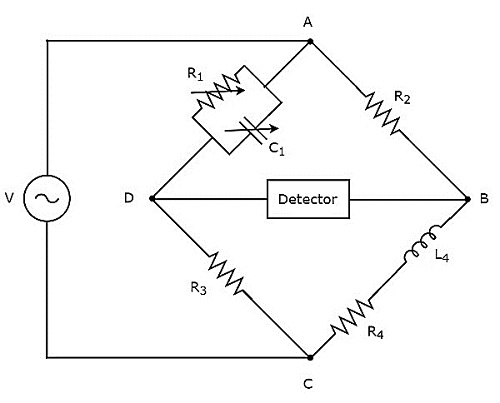
在上图电路中，AB、BC、CD和DA臂共同形成一个菱形或正方形。AB和CD臂分别包含电阻R₂和R₃。BC臂包含电阻R₄和电感L₄的串联组合。DA臂包含电阻R₁和电容C₁的并联组合。

设Z₁、Z₂、Z₃和Z₄分别是DA、AB、CD和BC臂的阻抗。**这些阻抗的值**将为

$$Z_{1}=\frac{R_{1}\left ( \frac{1}{j\omega C_{1}} \right )}{R_{1}+\frac{1}{j\omega C_{1}}}$$

$$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$$

$Z_{2}=R_{2}$

$Z_{3}=R_{3}$

$Z_{4}=R_{4}+j \omega L_{4}$

将这些阻抗值**代入**交流电桥的以下平衡条件。

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$$R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{\left ( {\frac{R_{1}}{1+j \omega R_{1}C_{1}}} \right )}$$

$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}\left (1+j \omega R_{1}C_{1} \right )}{R_{1}}$

$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+\frac{j \omega R_{1}C_{1}R_{2}R_{3}}{R_{1}}$

$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+j \omega C_{1}R_{2}R_{3}$

通过**比较**上式的相应实部和虚部，我们将得到

$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$公式 1

$L_{4}=C_{1}R_{2}R_{3}$公式 2

通过将电阻R₁、R₂和R₃的值代入公式 1，我们将得到电阻R₄的值。类似地，通过将电容C₁的值和电阻R₂和R₃的值代入公式 2，我们将得到电感L₄的值。

麦克斯韦电桥的**优点**是电阻R₄和电感L₄的值都与频率的值无关。

海电桥

海电桥是麦克斯韦电桥的改进版本，它是通过将包含电阻和电容并联组合的臂修改为包含电阻和电容串联组合的臂而得到的。

海氏电桥用于测量高电感的数值。海氏电桥的电路图如下所示。

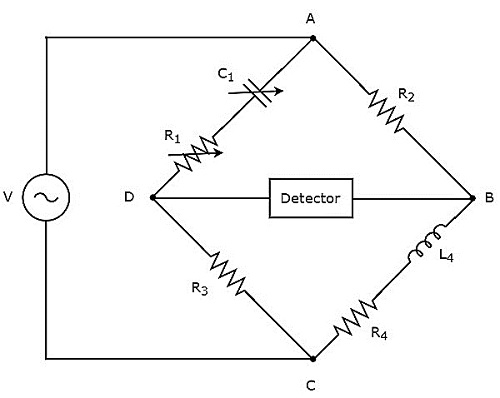
在上图电路中，AB、BC、CD和DA四臂构成菱形或正方形。AB和CD臂分别由电阻$R_{2}$和$R_{3}$组成。BC臂由电阻$R_{4}$和电感$L_{4}$串联组成。DA臂由电阻$R_{1}$和电容$C_{1}$串联组成。

设Z₁、Z₂、Z₃和Z₄分别是DA、AB、CD和BC臂的阻抗。**这些阻抗的值**将为

$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$

$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$

$Z_{2}=R_{2}$

$Z_{3}=R_{3}$

$Z_{4}=R_{4}+j \omega L_{4}$

将这些阻抗值**代入**交流电桥的以下平衡条件。

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}}{\left ( \frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}\right )}$

$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}$

将上式右边项的分子和分母都乘以$1 - j \omega R_{1}C_{1}$。

$\Rightarrow R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}\times \frac{\left (1 - j \omega R_{1}C_{1} \right )}{\left (1 - j \omega R_{1}C_{1} \right )}$

$\Rightarrow R_{4}+j \omega L_{4}=\frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}+j \omega R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$

通过**比较**上式的相应实部和虚部，我们将得到

$R_{4}= \frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$公式3

$L_{4}= \frac{R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$公式4

将$R_{1}, R_{2}, R_{3}, C_{1}$和$\omega$的值代入公式3和公式4，即可得到电阻$R_{4}$和电感$L_{4}$的值。

其他交流电桥

在上一章中，我们讨论了两种可用于测量电感的交流电桥。本章，让我们讨论以下两种交流电桥。

• Schering电桥
• Wien电桥

这两种电桥分别可以用来测量电容和频率。

Schering电桥

Schering电桥是一种具有四臂的交流电桥，四臂以菱形或正方形的形式连接，其中一臂由单个电阻组成，一臂由电阻和电容串联组成，一臂由单个电容组成，另一臂由电阻和电容并联组成。

交流检波器和交流电压源也用于查找未知阻抗的值，因此其中一个放置在Schering电桥的一条对角线上，另一个放置在Schering电桥的另一条对角线上。

Schering电桥用于测量电容的值。Schering电桥的电路图如下所示。

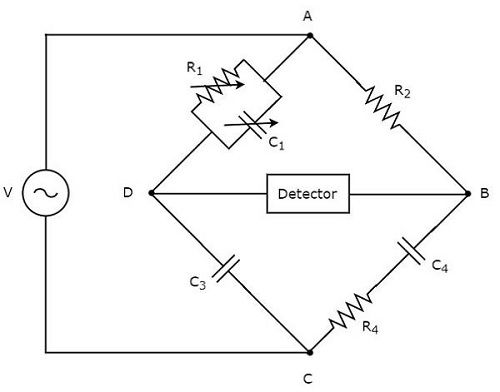
在上图电路中，AB、BC、CD和DA四臂构成菱形或正方形。AB臂由电阻$R_{2}$组成。BC臂由电阻$R_{4}$和电容$C_{4}$串联组成。CD臂由电容$C_{3}$组成。DA臂由电阻$R_{1}$和电容$C_{1}$并联组成。

设$Z_{1}$、$Z_{2}$、$Z_{3}$和$Z_{4}$分别为DA、AB、CD和BC臂的阻抗。这些阻抗的值将为

$Z_{1}=\frac{R_{1}\left ( \frac{1}{j \omega C_{1}} \right )}{R_{1}+\frac{1}{j \omega C_{1}}}$

$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$

$Z_{2}=R_{2}$

$Z_{3}=\frac{1}{j \omega C_{3}}$

$Z_{4}=R_{4}+\frac{1}{j \omega C_{4}}$

$\Rightarrow Z_{4}=\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}$

将这些阻抗值**代入**交流电桥的以下平衡条件。

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$$\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left (\frac{1}{j \omega C_{3}} \right )}{\frac{R_{1}}{1+j \omega R_{1}C_{1}}}$$

$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{j \omega R_{1}C_{3}}$

$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{R_{1}C_{3}}$

$\Rightarrow \frac{1}{C_{4}}+j \omega R_{4}=\frac{R_{2}}{R_{1}C_{3}}+\frac{j\omega C_{1}R_{2}}{C_{3}}$

通过**比较**上式的相应实部和虚部，我们将得到

$C_{4}=\frac{R_{1}C_{3}}{R_{2}}$公式1

$R_{4}=\frac{C_{1}R_{2}}{C_{3}}$公式2

将$R_{1}, R_{2}$和$C_{3}$的值代入公式1，即可得到电容$C_{4}$的值。类似地，将$R_{2}, C_{1}$和$C_{3}$的值代入公式2，即可得到电阻$R_{4}$的值。

Schering电桥的优点是电阻$R_{4}$和电容$C_{4}$的值都与频率无关。

Wien电桥

Wien电桥是一种具有四臂的交流电桥，四臂以菱形或正方形的形式连接。其中两臂由单个电阻组成，一臂由电阻和电容并联组成，另一臂由电阻和电容串联组成。

为了找到频率的值，还需要交流检波器和交流电压源。因此，这两个中的一个放置在Wien电桥的一条对角线上，另一个放置在Wien电桥的另一条对角线上。

Wien电桥的电路图如下所示。

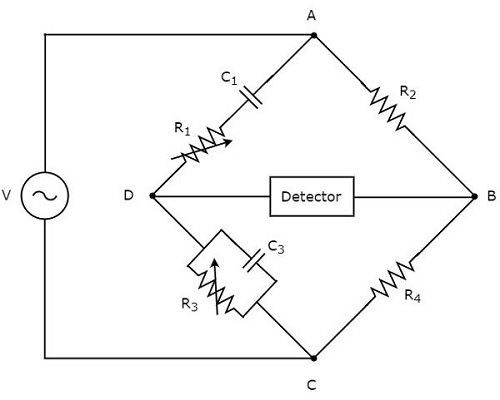
在上图电路中，AB、BC、CD和DA四臂构成菱形或正方形。AB和BC臂分别由电阻$R_{2}$和$R_{4}$组成。CD臂由电阻$R_{3}$和电容$C_{3}$并联组成。DA臂由电阻$R_{1}$和电容$C_{1}$串联组成。

设Z₁、Z₂、Z₃和Z₄分别是DA、AB、CD和BC臂的阻抗。**这些阻抗的值**将为

$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$

$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$

$Z_{2}=R_{2}$

$$Z_{3}=\frac{R_{3}\left (\frac{1}{j \omega C_{3}} \right )}{R_{3}+\frac{1}{j \omega C_{3}}}$$

$\Rightarrow Z_{3}= \frac{R_{3}}{1+j \omega R_{3}C_{3}}$

$Z_{4}=R_{4}$

将这些阻抗值**代入**交流电桥的以下平衡条件。

$$Z_{1}Z_{4}=Z_{2}Z_{3}$$

$\left (\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}} \right )R_{4}=R_{2}\left (\frac{R_{3}}{1+j \omega R_{3}C_{3}} \right )$$

$\Rightarrow \left (1+j \omega R_{1}C_{1}\right )\left (1+j \omega R_{3}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$

$\Rightarrow \left (1+j \omega R_{3}C_{3}+j \omega R_{1}C_{1}-\omega^{2}R_{1}R_{3}C_{1}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$

$\Rightarrow R_{4}\left ( \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )+j \omega R_{4}\left (R_{3}C_{3}+R_{1}C_{1} \right )=j \omega C_{1}R_{2}R_{3}$

等式上式中相应的实数项。

$$R_{4}\left (1- \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )=0$$

$\Rightarrow 1- \omega^{2}R_{1}R_{3}C_{1}C_{3} =0$

$\Rightarrow 1= \omega^{2}R_{1}R_{3}C_{1}C_{3}$

$\omega = \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$

代入$\omega = 2 \pi f$到上式中。

$\Rightarrow 2 \pi f= \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$

$\Rightarrow f= \frac{1}{2 \pi\sqrt{R_{1}R_{3}C_{1}C_{3}}}$

通过将$R_{1}, R_{3}, C_{1}$和$C_{3}$的值代入上式，我们可以找到交流电压源的频率$f$的值。

如果$R_{1}=R_{3}=R$且$C_{1}=C_{3}=C$，那么我们可以使用以下公式找到交流电压源的频率$f$的值。

$$f=\frac{1}{2\pi RC}$$

Wien电桥主要用于查找音频范围的频率值。

传感器

基本上，传感器将一种形式的能量转换为另一种形式的能量。将非电形式的能量转换为电形式的能量的传感器称为电传感器。电传感器的框图如下所示。

如图所示，电传感器将产生具有电能的输出。电传感器的输出等效于具有非电能的输入。

电传感器的类型

主要地，电传感器可以分为以下两种类型。

• 有源传感器
• 无源传感器

现在，让我们简要地讨论这两种类型的传感器。

有源传感器

能够产生电压和电流等电量的传感器称为有源传感器。它也称为自发传感器，因为它不需要任何外部电源。

有源传感器的框图如下所示。

如图所示，有源传感器将产生一个电量（或信号），该电量（或信号）等效于非电输入量（或信号）。

例子

以下是有源传感器的例子。

• 压电传感器
• 光电传感器
• 热电传感器

我们将在下一章讨论这些有源传感器。

无源传感器

不能产生电压和电流等电量的传感器称为无源传感器。但是，它会产生电阻(R)、电感(L)和电容(C)等无源元件的变化。无源传感器需要外部电源。

无源传感器的框图如下所示。

如图所示，无源传感器将根据非电输入量（或信号）的变化产生无源元件的变化。

例子

以下是无源传感器的例子。

• 电阻传感器
• 电感传感器
• 电容传感器

我们将在后面的章节中讨论这些无源传感器。

有源传感器

有源传感器是一种将非电量转换为电量的传感器。让我们考虑诸如压力、光照度和温度等非电量。因此，根据我们选择的非电量，我们将得到以下三种有源传感器。

• 压电传感器
• 光电传感器
• 热电传感器

现在，让我们逐一讨论这三种有源传感器。

压电传感器

当有源传感器产生等效于压力输入的电量时，则称为压电传感器。以下三种物质表现出压电效应。

• 石英
• 罗谢尔盐
• 电气石

这三种物质表现出的压电效应依次为电气石、石英和罗谢尔盐。这三种物质的机械强度依次为罗谢尔盐、石英、电气石。

石英用作压电传感器，因为它在这三种压电物质中表现出适中的压电效应并且具有适中的机械强度。

石英传感器

石英传感器的电路图如下所示。如图所示，石英晶体置于底座和合力构件之间。输出电压可以在放置在石英晶体两侧的金属电极上测量。

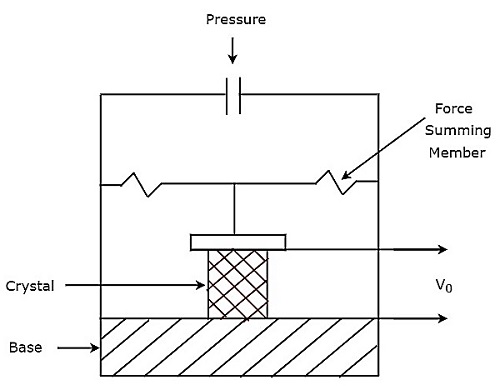
上述压力传感器的输出电压$V_{0}$将为

$$V_{0}=\frac{Q}{C}$$

光电传感器

当有源传感器产生等效于光照度输入的电量时，则称为光电传感器。光电传感器的电路图如下所示。

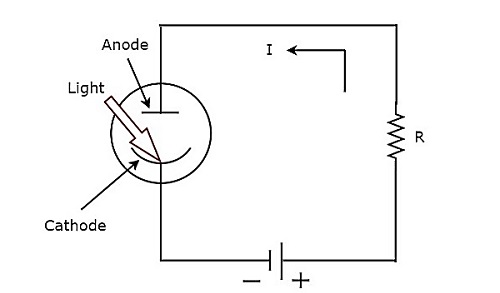
光电传感器的工作原理如下所述。

• 步骤1 - 当光线照射到光电传感器的阴极上时，它会释放电子。

• 步骤2 - 由于电子被吸引到阳极，光电传感器会在电路中产生电流I。

我们可以使用以下公式找到光电传感器的灵敏度。

$$S=\frac{I}{i}$$

其中，

$S$是光电传感器的灵敏度

$I$是光电传感器的输出电流

$i$是光电传感器的光照度输入

热电传感器

当有源传感器产生等效于温度输入的电量时，则称为热电传感器。以下两种传感器是热电传感器的例子。

• 热敏电阻传感器
• 热电偶传感器

现在，让我们逐一讨论这两种传感器。

热敏电阻传感器

取决于温度的电阻称为热电阻。简称为热敏电阻。热敏电阻的温度系数为负。这意味着随着温度升高，热敏电阻的阻值降低。

在数学上，热敏电阻的电阻与温度之间的关系可以表示为

$$R_{1}=R_{2}e^\left ( \beta \left [ \frac{1}{T_{1}}-\frac{1}{T_{2}} \right ] \right )$$

其中,

$R_{1}$ 是热敏电阻在温度 ${T_{1}}^{0}K$ 时的电阻

$R_{2}$ 是热敏电阻在温度 ${T_{2}}^{0}K$ 时的电阻

$\beta$ 是温度常数

热敏电阻传感器的优点是它可以产生快速稳定的响应。

热电偶传感器

热电偶传感器产生与输入温度变化相对应的输出电压。如果将两种不同金属的导线连接在一起以创建两个结点，则整个配置称为热电偶。基本热电偶的电路图如下所示：

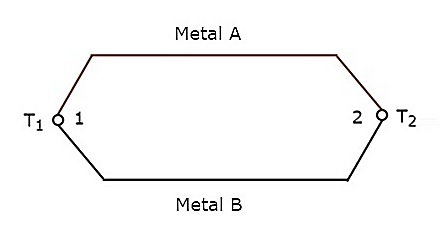
上述热电偶具有两种金属 A 和 B 以及两个结点 1 和 2。考虑结点 2 处的恒定参考温度 $T_{2}$。设结点 1 处的温度为 $T_{1}$。热电偶产生电动势（电动势），只要 $T_{1}$ 和 $T_{2}$ 的值不同。

这意味着，只要两个结点 1 和 2 之间存在温差，热电偶就会产生电动势，并且它与这两个结点之间的温差成正比。在数学上，它可以表示为

$$e \alpha \left ( T_{1}-T_{2} \right )$$

其中，

$e$ 是热电偶产生的电动势

上述热电偶电路可以表示为下图所示，用于实际应用。

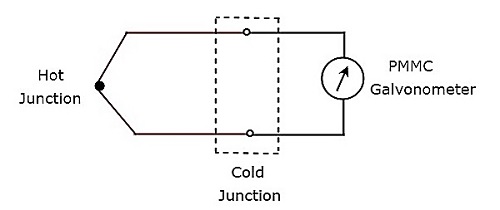
电路的一部分，位于热结点和冷结点之间，包括这两个结点，是基本热电偶的等效模型。一个 PMMC 电流计连接在冷结点上，它根据冷结点上产生的电动势偏转。热电偶传感器是最常用的热电传感器。

无源传感器

无源传感器是一种传感器，它产生无源元件的变化。我们将考虑电阻、电感和电容等无源元件。因此，根据我们选择的无源元件，我们将得到以下三种无源传感器。

• 电阻传感器
• 电感传感器
• 电容传感器

现在，让我们逐一讨论这三种无源传感器。

电阻传感器

当无源传感器产生电阻值的变异（变化）时，它被称为电阻传感器。金属导体的电阻 R 的公式如下。

$$R=\frac{\rho \:l}{A}$$

其中，

$\rho$ 是导体的电阻率

$l$ 是导体的长度

$A$ 是导体的横截面积

电阻值取决于三个参数 $\rho, l$ 和 $A$。因此，我们可以根据三个参数 $\rho, l$ 和 $A$ 中的一个的变化来制作电阻传感器。这三个参数中的任何一个的变化都会改变电阻值。

• 电阻 R 与导体的电阻率 $\rho$ 成正比。因此，随着导体电阻率 $\rho$ 的增加，电阻 R 的值也增加。类似地，随着导体电阻率 $\rho$ 的降低，电阻 R 的值也降低。

• 电阻 R 与导体的长度 $l$ 成正比。因此，随着导体长度 $l$ 的增加，电阻 R 的值也增加。类似地，随着导体长度 $l$ 的降低，电阻 R 的值也降低。

• 电阻 R 与导体的横截面积 $A$ 成反比。因此，随着导体横截面积 $A$ 的增加，电阻 R 的值降低。类似地，随着导体横截面积 $A$ 的降低，电阻 R 的值增加。

电感传感器

当无源传感器产生电感值的变异（变化）时，它被称为电感传感器。电感器的电感 L 的公式如下。

$L=\frac{N^{2}}{S}$公式 1

其中，

$N$ 是线圈的匝数

$S$ 是线圈的匝数

线圈的磁阻 S 的公式如下。

$S=\frac{l}{\mu A}$公式 2

其中，

$l$ 是磁路的长度

$\mu$ 是磁芯的磁导率

$A$ 是磁通通过的磁路面积

将公式 2 代入公式 1。

$$L=\frac{N^{2}}{\left (\frac{l}{\mu A} \right )}$$

$\Rightarrow L=\frac{N^{2}\mu A}{l}$公式 3

从公式 1 和公式 3，我们可以得出结论，电感值取决于三个参数 $N,S$ 和 $\mu$。因此，我们可以根据三个参数 $N,S$ 和 $\mu$ 中的一个的变化来制作电感传感器。因为，这三个参数中的任何一个的变化都会改变电感值。

• 电感 L 与线圈匝数的平方成正比。因此，随着线圈匝数 $N$ 的增加，电感 $L$ 的值也增加。类似地，随着线圈匝数 $N$ 的减少，电感 $L$ 的值也减少。

• 电感 $L$ 与线圈的磁阻 $S$ 成反比。因此，随着线圈磁阻 $S$ 的增加，电感 $L$ 的值减小。类似地，随着线圈磁阻 $S$ 的减小，电感 $L$ 的值增加。

• 电感 L 与磁芯的磁导率 $\mu$ 成正比。因此，随着磁芯磁导率 $\mu$ 的增加，电感 L 的值也增加。类似地，随着磁芯磁导率 $\mu$ 的减少，电感 L 的值也减少。

电容传感器

当无源传感器产生电容值的变异（变化）时，它被称为电容传感器。平行板电容器的电容 C 的公式如下。

$$C=\frac{\varepsilon A}{d}$$

其中，

$\varepsilon$ 是介电常数或介电常数

$A$ 是两个极板的有效面积

$d$ 是两个极板的有效面积

电容值取决于三个参数 $\varepsilon, A$ 和 $d$。因此，我们可以根据三个参数 $\varepsilon, A$ 和 $d$ 中的一个的变化来制作电容传感器。因为，这三个参数中的任何一个的变化都会改变电容值。

• 电容 C 与介电常数 $\varepsilon$ 成正比。因此，随着介电常数 $\varepsilon$ 的增加，电容 C 的值也增加。类似地，随着介电常数 $\varepsilon$ 的减少，电容 C 的值也减少。

• 电容 C 与两个极板的有效面积 $A$ 成正比。因此，随着两个极板的有效面积 $A$ 的增加，电容 C 的值也增加。类似地，随着两个极板的有效面积 $A$ 的减少，电容 C 的值也减少。

• 电容 C 与两个极板之间的距离 $d$ 成反比。因此，随着两个极板之间距离 $d$ 的增加，电容 C 的值减小。类似地，随着两个极板之间距离 $d$ 的减少，电容 C 的值增加。

在本章中，我们讨论了三种无源传感器。在下一章中，让我们讨论每个无源传感器的示例。

位移测量

诸如位移、速度、力、温度等物理量都是非电量。有源传感器将物理量转换为电信号。而无源传感器将物理量转换为无源元件的变化。

因此，根据需求，我们可以选择有源传感器或无源传感器。在本章中，让我们讨论如何使用无源传感器测量位移。如果一个物体沿直线从一个点移动到另一个点，则这两个点之间的长度称为位移。

我们有以下三种无源传感器

• 电阻传感器
• 电感传感器
• 电容传感器

现在，让我们逐一讨论使用这三种无源传感器测量位移。

使用电阻传感器测量位移

用于测量位移的电阻传感器的电路图如下所示。

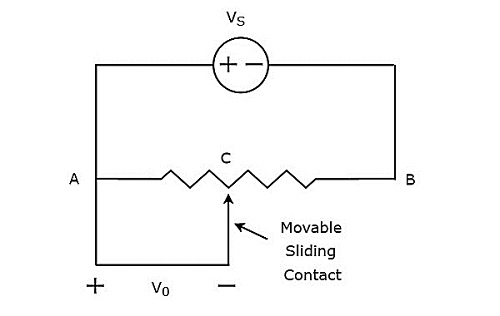
上述电路由一个电位器和一个电压源 $V_{S}$ 组成。我们可以说这两个是相对于 A 和 B 点并联连接的。电位器有一个可以变化的滑动触点。因此，C 点是一个可变点。在上述电路中，输出电压 $V_{0}$ 是在 A 和 C 点之间测量的。

在数学上，电压和距离之间的关系可以表示为

$$\frac{V_{0}}{V_{S}}=\frac{AC}{AB}$$

因此，我们应该将需要测量其位移的物体连接到滑动触点。因此，无论何时物体沿直线移动，C 点也会发生变化。因此，输出电压 $V_{0}$ 也相应地发生变化。

在这种情况下，我们可以通过测量输出电压 $V_{0}$ 来找到位移。

使用电感传感器测量位移

用于测量位移的电感传感器的电路图如下所示。

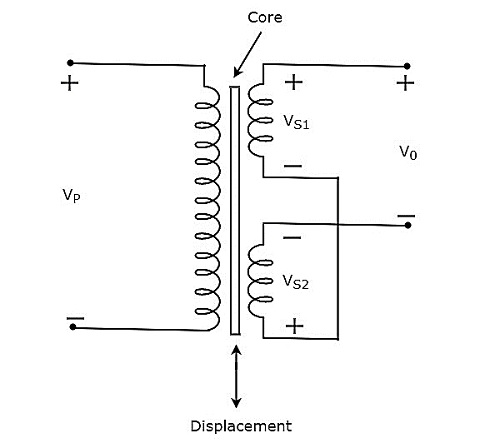
上述电路中存在的变压器具有一个初级绕组和两个次级绕组。在这里，两个次级绕组的端点连接在一起。因此，我们可以说这两个次级绕组是反向串联连接的。

电压 $V_{P}$ 加在变压器的初级绕组上。设每个次级绕组上产生的电压为 𠑉𠑆1 和 𠑉𠑆2。输出电压 $V_{0}$ 取自两个次级绕组的起点。

在数学上，输出电压 𠑉0 可以写成

$$V_{0}= V_{S1}-V_{S2}$$

上述电路中存在的变压器称为差动变压器，因为它产生一个输出电压，该电压是 $V_{S1}$ 和 $V_{S2}$ 之间的差值。

• 如果铁芯位于中心位置，则输出电压 $V_{0}$ 将等于零。因为，$V_{S1}$ 和 $V_{S2}$ 的幅值和相位相同。

• 如果铁芯不在中心位置，则输出电压 $V_{0}$ 将具有一定的幅值和相位。因为，$V_{S1}$ 和 $V_{S2}$ 的幅值和相位不相等。

因此，我们应该将需要测量其位移的物体连接到中心铁芯。因此，无论何时物体沿直线移动，铁芯的中心位置都会发生变化。因此，输出电压 $V_{0}$ 也相应地发生变化。

在这种情况下，我们可以通过测量输出电压 $V_{0}$ 来找到位移。输出电压 $V_{0}$ 的幅值和相位分别表示物体的位移及其方向。

使用电容传感器测量位移

用于测量位移的电容传感器的电路图如下所示。

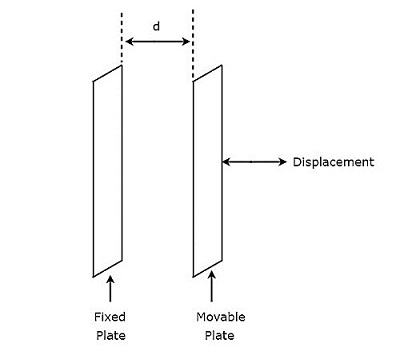
上述电路中存在的电容器有两个平行板。其中一块是固定的，另一块是可以移动的。因此，这两个极板之间的间距也会发生变化。随着电容器两个极板之间间距的变化，电容值也会发生变化。

因此，我们应该将需要测量其位移的物体连接到电容器的可动极板上。因此，无论何时物体沿直线移动，电容器两个极板之间的间距都会发生变化。因此，电容值发生变化。

数据采集系统

用于数据采集的系统称为数据采集系统。这些数据采集系统将执行诸如数据转换、数据存储、数据传输和数据处理等任务。

数据采集系统考虑以下模拟信号。

• 从直流和交流电压、直流和交流电流、电阻等电量的直接测量获得的模拟信号。

• 从诸如 LVDT、热电偶等传感器获得的模拟信号。

数据采集系统的类型

数据采集系统可以分为以下两种类型。

• 模拟数据采集系统
• 数字数据采集系统

现在，让我们逐一讨论这两种类型的数据采集系统。

模拟数据采集系统

可以使用模拟信号操作的数据采集系统称为模拟数据采集系统。以下是模拟数据采集系统的模块。

• 传感器 - 它将物理量转换为电信号。

• 信号调理器 - 它执行诸如放大和选择信号所需部分的功能。

• 显示设备 - 它显示输入信号以进行监控。

• 图形记录仪器 - 这些可以用来永久记录输入数据。

• 磁带仪器 - 用于获取、存储和再现输入数据。

数字数据采集系统

可以使用数字信号操作的数据采集系统被称为数字数据采集系统。因此，它们使用数字组件来存储或显示信息。

主要地在数字数据采集中发生以下操作。

• 模拟信号采集
• 模拟信号转换为数字信号或数字数据
• 数字信号或数字数据的处理

以下是数字数据采集系统的模块。

• 传感器 - 它将物理量转换为电信号。

• 信号调理器 - 它执行诸如放大和选择信号所需部分的功能。

• 多路复用器 - 将多个输入中的一个连接到输出。因此，它充当并行到串行的转换器。

• 模数转换器 - 它将模拟输入转换为其等效的数字输出。

• 显示设备 - 它以数字格式显示数据。

• 数字记录器 - 用于以数字格式记录数据。

数据采集系统已广泛应用于生物医学和航空航天等领域。因此，我们可以根据需要选择模拟数据采集系统或数字数据采集系统。