
直流电桥
直流电桥只能使用直流电压信号进行操作。直流电桥用于测量桥路中未知电阻的值。惠斯通电桥是直流电桥的一个例子。
现在,让我们讨论一下惠斯通电桥,以找到未知电阻的值。
惠斯通电桥
惠斯通电桥是一种简单的直流电桥,主要有四个臂。这四个臂形成菱形或正方形,每个臂包含一个电阻。
为了找到未知电阻的值,我们需要检流计和直流电压源。因此,这两个中的一个放置在惠斯通电桥的一个对角线上,另一个放置在惠斯通电桥的另一个对角线上。
惠斯通电桥用于测量中等电阻的值。惠斯通电桥的电路图如下所示。
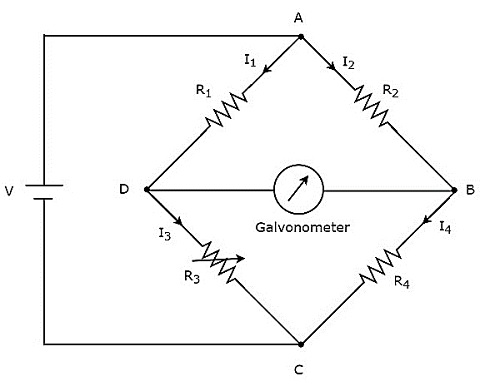
在上面的电路中,臂AB、BC、CD和DA共同形成菱形或正方形。它们分别包含电阻$R_{2}$、$R_{4}$、$R_{3}$和$R_{1}$。设流过这些电阻臂的电流分别为$I_{2}$、$I_{4}$、$I_{3}$和$I_{1}$,这些电流的方向如图所示。
对角线臂DB和AC分别包含检流计和V伏的直流电压源。这里,电阻$R_{3}$是一个标准的可变电阻,电阻$R_{4}$是一个未知电阻。我们可以通过改变电阻$R_{3}$的阻值来平衡电桥。
当没有电流流过对角线臂DB时,上述桥路电路处于平衡状态。这意味着,当电桥平衡时,检流计没有偏转。
当满足以下两个条件时,电桥将处于平衡状态。
臂AD上的电压等于臂AB上的电压。即
$$V_{AD}=V_{AB}$$
$\Rightarrow I_{1}R_{1}=I_{2}R_{2}$公式1
臂DC上的电压等于臂BC上的电压。即
$$V_{DC}=V_{BC}$$
$\Rightarrow I_{3}R_{3}=I_{4}R_{4}$公式2
根据以上两个平衡条件,我们将得到以下两个结论。
流过臂AD的电流将等于臂DC的电流。即
$$I_{1}=I_{3}$$
流过臂AB的电流将等于臂BC的电流。即
$$I_{2}=I_{4}$$
取公式1和公式2的比率。
$\frac{I_{1}R_{1}}{I_{3}R_{3}}=\frac{I_{2}R_{2}}{I_{4}R_{4}}$公式3
在公式3中代入$I_{1}=I_{3}$和$I_{2}=I_{4}$。
$$\frac{I_{3}R_{1}}{I_{3}R_{3}}=\frac{I_{4}R_{2}}{I_{4}R_{4}}$$
$$\Rightarrow \frac{R_{1}}{R_{3}}=\frac{R_{2}}{R_{4}}$$
$$\Rightarrow R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$
通过将已知电阻$R_{1}$、$R_{2}$和$R_{3}$的值代入上式,我们将得到电阻$R_{4}$的值。