叠加定理解释

叠加定理用于解决存在两个或多个电源且不串联或并联连接的网络。

叠加定理的陈述

如果两个或多个电压或电流源同时作用在一个线性网络中，则任何支路中的合成电流是当每个电源单独作用且所有其他独立电源被其内阻替换时，该支路中产生的电流的代数和。

叠加定理的解释

在下图所示电路中，我们必须使用叠加定理求解支路电流i₁、i₂、i₃。

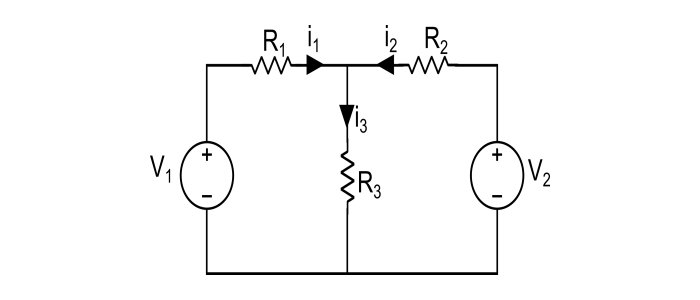
步骤 1 – 首先只考虑电源 V₁，将 V₂ 替换为短路。

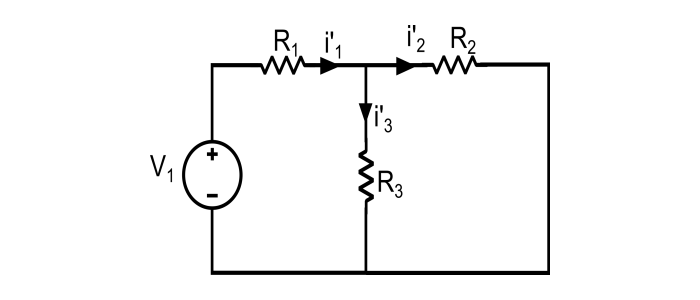
这里，支路电流 i’₁、i’₂、i’₃ 为：

$$i'_{1}=\frac{V_{1}}{\frac{R_{2}R_{3}}{R_{2}+R_{3}}+R_{1}}$$

$$i'_{2}=i'_{1}\frac{R_{3}}{R_{2}+R_{3}}$$

$$i'_{3}=i'_{1}-i'_{2}$$

步骤 2 – 只考虑电源 V₂，将 V₁ 替换为短路。

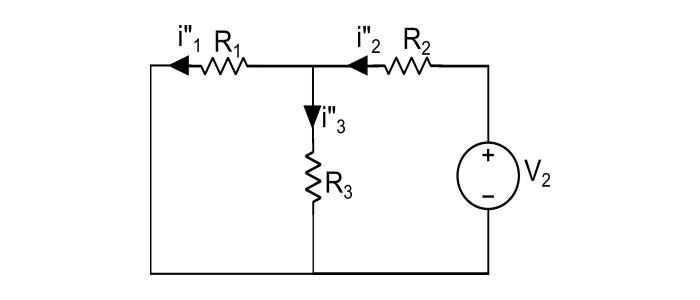
这里，支路电流 i"₁、i"₂、i"₃ 为：

$$i"_{2}=\frac{V_{2}}{\frac{R_{1}R_{3}}{R_{1}+R_{3}}+R_{2}}$$

$$i"_{2}=i"_{2}\frac{R_{3}}{R_{1}+R_{3}}$$

$$i"_{3}=i"_{2}-i"_{1}$$

步骤 3 – 应用叠加定理：

$$i_{1}=i'_{1}-i"_{1}$$

$$i_{2}=i"_{2}-i'_{1}$$

$$i_{3}=i'_{3}+i"_{3}$$

注意 – 在应用叠加定理时，应注意每个电源计算出的电流的方向。

使用叠加定理求解网络的步骤

步骤 1 – 只取一个独立电源，并使其他独立电源失效（电压源用短路替换，电流源用开路替换）。获得支路电流。

步骤 2 – 对每个独立电源重复步骤 1。

步骤 3 – 要使用叠加定理确定净支路电流，请将步骤 1 和步骤 2 中获得的每个支路的电流相加。如果步骤 1 和步骤 2 中获得的电流方向相同，则将其相加；如果各个电流在每个步骤中的方向相反，则以原始电流的方向为参考，并减去相反方向的电流。然后计算每个支路的净电流。

数值示例

在下图所示电路中，V_s = 0，I = 4 A；求 V_s = 20 V 时的 I。

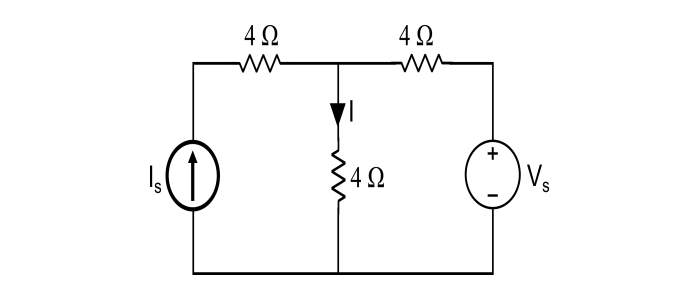
解决方案

步骤 1 – 当 V_s = 0 即短路且 Is 单独作用时，

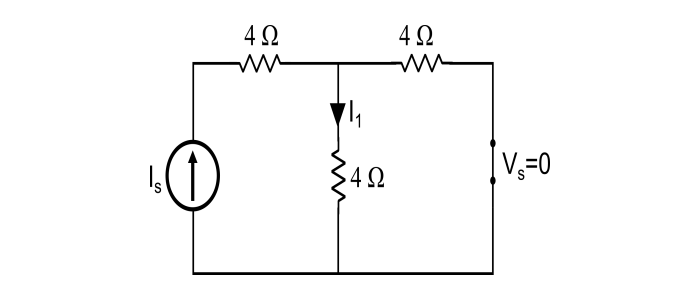
$$I_{1}=4A\:(已知)$$

步骤 2 – 当 V_s = 20 V 且 Is 失效时，

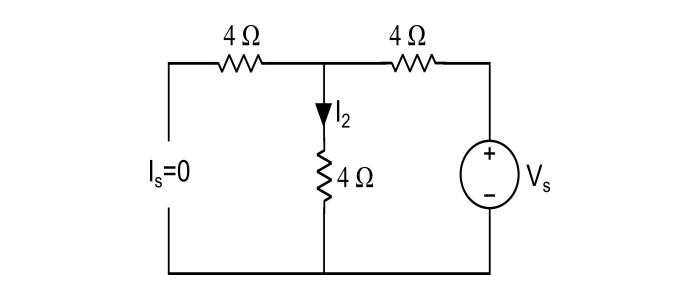
$$I_{2}=\frac{20}{4+4}=2.5A$$

因此，应用叠加定理，净电流 (I) 为：

$$I=I_{1}+I_{2}=4+2.5=6.5A$$

Manish Kumar Saini

更新于：2021年5月29日

15K+ 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习