最大功率传输定理

最大功率传输定理 (MPT) 用于查找负载电阻的值，在此值下，从电源到负载的功率传输量最大。

MPT 的陈述

连接到直流电源的电阻负载，当负载电阻等于从负载端子看到的电源的内部电阻时，接收到的功率最大。

MPT 的解释

考虑以下电路图，以确定 R_L 的值，以便它从直流电源接收最大功率。

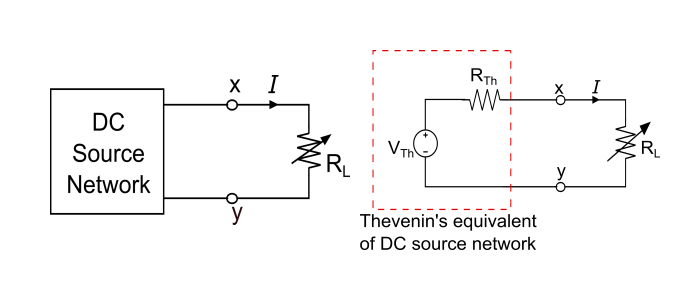
负载电流为：

$$I=\frac{V_{Th}}{R_{Th}+R_{L}}$$

因此，传递到电阻负载的功率为：

$$P_{L}=I^{2}R_{L}=(\frac{V_{Th}}{R_{Th}+R_{L}})^{2}R_{L}$$

众所周知，负载电阻是可变的。因此，可以通过改变 R_L 来最大化 P_L。

$$\Rightarrow\:P_{L}=\frac{V_{Th}^{2}R_{L}}{(R_{th}+R_{L})^{2}}=\frac{V_{Th}^{2}R_{L}}{R_{Th}^{2}+R_{L}^{2}+2R_{Th}R_{L}}$$

$$\Rightarrow\:P_{L}=\frac{V_{Th}^{2}}{(\frac{R_{th}^{2}}{R_{L}}+R_{L}+2R_{Th})}=\frac{V_{Th}^{2}}{D}$$

为了使 PL 最大化，分母 (D) 项应最小，即：

$$\frac{dD}{dR_{L}}=0$$

$$\frac{d}{dR_{L}}(\frac{R_{Th}^{2}}{R_{L}}+R_{L}+2R_{Th})=0$$

通过求解上述微分方程，我们得到：

$$R_{L}=R_{Th}$$

因此，如果负载电阻等于源网络的内部电阻，则最大功率将传递到负载，即：

负载电阻 = 源的内部电阻

最大功率 (Pmax) 的量

$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}$$

这里，Pmax 是负载消耗的最大功率量。

电源提供的总功率为

$$P=2\frac{V_{Th}^{2}}{4R_{Th}}=\frac{V_{Th}^{2}}{2R_{Th}}$$

在最大功率传输期间电路的效率变为：

$$\eta=\frac{P_{max}}{P}\times\:100=50$$ %

使用 MPT 求解网络的步骤

步骤 1 – 去除负载电阻，并将所有独立电源替换为它们的内部电阻，并确定从开路负载端子观察源网络的 R_Th。

步骤 2 – 根据 MPT，R_Th 的值给出负载电阻 R_L 的值，即 R_Th = R_L，这允许最大功率传输。

步骤 3 – 找到开路负载端子上的 V_Th 值。

步骤 4 – 传输的最大功率量由下式给出：

$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}$$

数值示例

求下图所示电路中负载电阻 R_L 的值，使功率最大传输。并计算最大功率值。

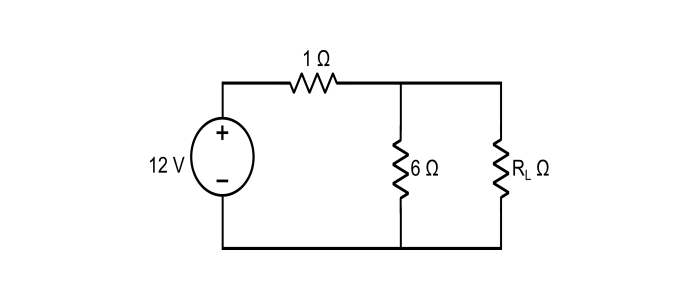
解决方案

步骤 1 – 去除负载电阻，并将所有独立电源替换为它们的内部电阻（在本例中，12 V 理想电压源短路），并确定给出与最大功率传输对应的 RL 的 RTh 值。

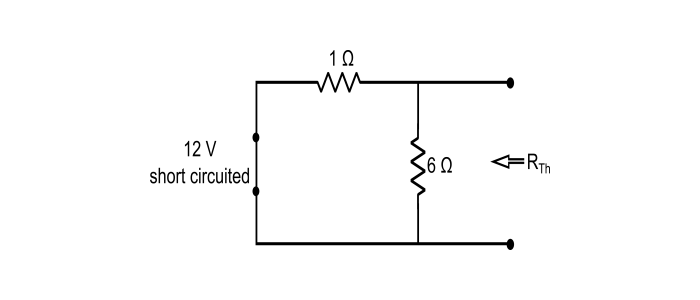
$$R_{Th}=1\:\Omega\:\lVert\:6\:\Omega=\frac{1\times\:6}{1+\:6}=\frac{6}{7}\:\Omega$$

根据最大功率传输定理：

$$R_{L}=R_{Th}=\frac{6}{7}\:\Omega$$

步骤 2 – 确定开路负载端子上的 VTh，

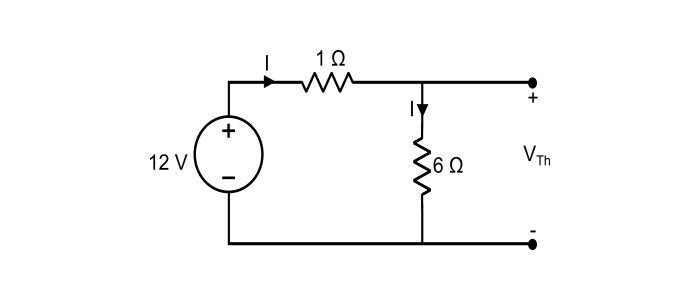
这里，电路中的电流为：

$$I=\frac{12}{1+6}=\frac{12}{7}\:安培$$

由于负载端子是开路的，因此 V_Th 是 6 Ω 电阻上的电压降。因此，

$$V_{Th}=I\times\:6\Omega=\frac{12}{7}\times\:6=\frac{72}{7}\:伏特$$

传递到负载的最大功率量为：

$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}=\frac{(72/7)^{2}}{4\times\:(6/7)}=30.857瓦特$$

因此，最大功率传输的负载电阻值为 (6/7 Ω)，传递到负载的最大功率为 30.857 瓦特。

Saini Manish Kumar

更新于：2021年6月8日

577 次查看

开启你的职业生涯

通过完成课程获得认证

开始学习