分类算法 - 逻辑回归

上一页
下一页

逻辑回归介绍

逻辑回归是一种监督学习分类算法，用于预测目标变量的概率。目标变量或因变量的性质是二分的，这意味着只有两种可能的类别。

简单来说，因变量本质上是二元的，数据编码为1（代表成功/是）或0（代表失败/否）。

在数学上，逻辑回归模型预测P(Y=1)作为X的函数。它是可用于各种分类问题的最简单的机器学习算法之一，例如垃圾邮件检测、糖尿病预测、癌症检测等。

逻辑回归的类型

通常，逻辑回归是指具有二元目标变量的二元逻辑回归，但它还可以预测目标变量的另外两个类别。根据这些类别的数量，逻辑回归可以分为以下类型：

二元或二项

在这种类型的分类中，因变量只有两种可能的类型，要么是1，要么是0。例如，这些变量可以代表成功或失败、是或否、赢或输等。

多项

在这种类型的分类中，因变量可以有3种或更多种可能的无序类型，或者这些类型没有定量意义。例如，这些变量可以代表“A型”、“B型”或“C型”。

有序

在这种类型的分类中，因变量可以有3种或更多种可能的顺序类型，或者这些类型具有定量意义。例如，这些变量可以代表“差”、“好”、“非常好”、“优秀”，每个类别可以有0,1,2,3这样的分数。

逻辑回归假设

在深入研究逻辑回归的实现之前，我们必须了解以下关于它的假设：

  • 在二元逻辑回归的情况下，目标变量必须始终是二元的，并且期望的结果由因子水平1表示。

  • 模型中不应存在多重共线性，这意味着自变量必须彼此独立。

  • 我们必须在模型中包含有意义的变量。

  • 我们应该为逻辑回归选择一个大的样本量。

二元逻辑回归模型

逻辑回归最简单的形式是二元或二项逻辑回归，其中目标变量或因变量只有两种可能的类型，要么是1，要么是0。它允许我们模拟多个预测变量和二元/二项目标变量之间的关系。在逻辑回归的情况下，线性函数基本上用作另一个函数（例如以下关系中的g）的输入：

$$h_{\theta}{(x)}=g(\theta^{T}x)𝑤ℎ𝑒𝑟𝑒 0≤h_{\theta}≤1$$

这里，g是逻辑函数或S型函数，可以表示如下：

$$g(z)= \frac{1}{1+e^{-z}}𝑤ℎ𝑒𝑟𝑒 𝑧=\theta ^{T}𝑥$$

S型曲线可以用下图表示。我们可以看到y轴的值介于0和1之间，并在0.5处穿过轴。

Flow

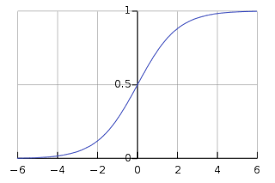
类别可以分为正类或负类。如果输出介于0和1之间，则输出属于正类的概率。在我们的实现中，如果假设函数的输出≥0.5，则将其解释为正类，否则为负类。

我们还需要定义一个损失函数来衡量算法使用函数权重（用θ表示）的性能，如下所示：

ℎ=𝑔(𝑋𝜃)

$$J(\theta) = \frac{1}{m}.(-y^{T}log(h) - (1 -y)^Tlog(1-h))$$

现在，在定义了损失函数之后，我们的主要目标是最小化损失函数。这可以通过拟合权重来完成，这意味着增加或减少权重。借助损失函数相对于每个权重的导数，我们将能够知道哪些参数应该具有较高的权重，哪些参数应该具有较低的权重。

下面的梯度下降方程告诉我们如果修改参数，损失将如何变化：

$$\frac{𝛿𝐽(𝜃)}{𝛿\theta_{j}}=\frac{1}{m}X^{T}(𝑔(𝑋𝜃)−𝑦)$$

Python实现

现在，我们将用Python实现上述二元逻辑回归的概念。为此，我们使用一个名为“iris”的多元花卉数据集，它包含3个类别，每个类别有50个实例，但我们将使用前两个特征列。每个类别代表一种鸢尾花。

首先，我们需要导入必要的库，如下所示：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets

接下来，加载iris数据集，如下所示：

iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1

我们可以绘制我们的训练数据，如下所示：

plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();
Star

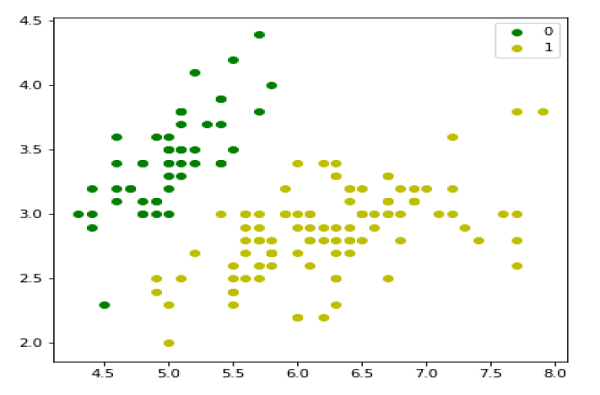
接下来，我们将定义sigmoid函数、损失函数和梯度下降，如下所示：

class LogisticRegression:
   def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
      self.lr = lr
      self.num_iter = num_iter
      self.fit_intercept = fit_intercept
      self.verbose = verbose
   def __add_intercept(self, X):
      intercept = np.ones((X.shape[0], 1))
      return np.concatenate((intercept, X), axis=1)
   def __sigmoid(self, z):
      return 1 / (1 + np.exp(-z))
   def __loss(self, h, y):
      return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
   def fit(self, X, y):
      if self.fit_intercept:
         X = self.__add_intercept(X)

现在，初始化权重，如下所示：

self.theta = np.zeros(X.shape[1])
   for i in range(self.num_iter):
      z = np.dot(X, self.theta)
      h = self.__sigmoid(z)
      gradient = np.dot(X.T, (h - y)) / y.size
      self.theta -= self.lr * gradient
      z = np.dot(X, self.theta)
      h = self.__sigmoid(z)
      loss = self.__loss(h, y)
      if(self.verbose ==True and i % 10000 == 0):
         print(f'loss: {loss} \t')

借助以下脚本，我们可以预测输出概率：

def predict_prob(self, X):
   if self.fit_intercept:
      X = self.__add_intercept(X)
   return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
   return self.predict_prob(X).round()

接下来，我们可以评估模型并绘制它，如下所示：

model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()

plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
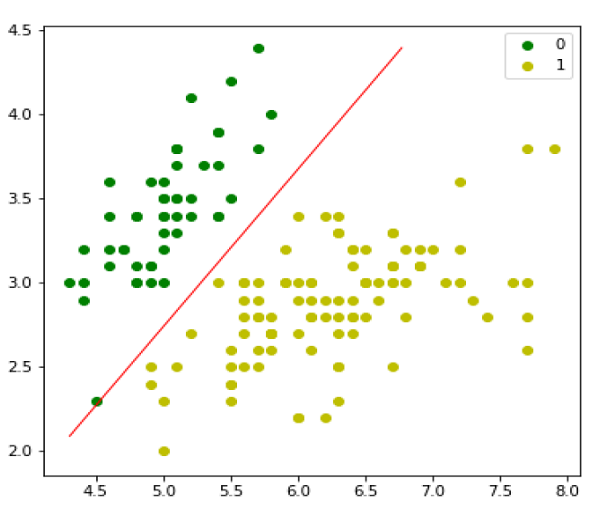
Red Line

多项逻辑回归模型

逻辑回归的另一种有用的形式是多项逻辑回归，其中目标变量或因变量可以有3种或更多种可能的无序类型，即没有定量意义的类型。

Python实现

现在，我们将用Python实现上述多项逻辑回归的概念。为此，我们使用sklearn中的一个名为digit的数据集。

首先，我们需要导入必要的库，如下所示：

Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_split

接下来，我们需要加载digit数据集：

digits = datasets.load_digits()

现在，定义特征矩阵(X)和响应向量(y)，如下所示：

X = digits.data
y = digits.target

借助下一行代码，我们可以将X和y拆分为训练集和测试集：

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)

现在，创建一个逻辑回归对象，如下所示：

digreg = linear_model.LogisticRegression()

现在，我们需要使用训练集来训练模型，如下所示：

digreg.fit(X_train, y_train)

接下来，对测试集进行预测，如下所示：

y_pred = digreg.predict(X_test)

接下来，打印模型的准确率，如下所示：

print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)

输出

Accuracy of Logistic Regression model is: 95.6884561891516

从上面的输出中，我们可以看到我们的模型的准确率约为96%。

打印页面
上一页
下一页
广告