回归算法 - 线性回归

---

---

线性回归介绍

线性回归可以定义为分析因变量与一组给定自变量之间线性关系的统计模型。变量之间的线性关系意味着，当一个或多个自变量的值发生变化（增加或减少）时，因变量的值也会相应地发生变化（增加或减少）。

数学上，这种关系可以用以下等式表示：

Y = mX + b

这里，Y是我们试图预测的因变量

X 是我们用来进行预测的自变量。

m 是回归线的斜率，表示 X 对 Y 的影响

b 是一个常数，称为 Y 截距。如果 X = 0，则 Y 等于 b。

此外，线性关系可以是正的或负的，如下所述：

正线性关系

如果自变量和因变量都增加，则线性关系称为正线性关系。这可以通过下图理解：

负线性关系

如果自变量增加而因变量减少，则线性关系称为负线性关系。这可以通过下图理解：

线性回归的类型

线性回归分为以下两种类型：

• 简单线性回归
• 多元线性回归

简单线性回归 (SLR)

这是线性回归最基本的版本，它使用单个特征来预测响应。SLR 的假设是这两个变量之间存在线性关系。

Python 实现

我们可以通过两种方式在 Python 中实现 SLR，一种是提供您自己的数据集，另一种是使用 scikit-learn Python 库中的数据集。

示例 1 - 在下面的 Python 实现示例中，我们使用我们自己的数据集。

首先，我们将从导入必要的包开始：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

接下来，定义一个函数，该函数将计算 SLR 的重要值：

def coef_estimation(x, y):

以下脚本行将给出观察值的数量 n：

n = np.size(x)

x 和 y 向量的均值可以计算如下：

m_x, m_y = np.mean(x), np.mean(y)

我们可以找到关于 x 的交叉偏差和偏差：

SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x

接下来，回归系数，即 b，可以计算如下：

b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)

接下来，我们需要定义一个函数，该函数将绘制回归线，并将预测响应向量：

def plot_regression_line(x, y, b):

以下脚本行将实际点绘制为散点图：

plt.scatter(x, y, color = "m", marker = "o", s = 30)

以下脚本行将预测响应向量：

y_pred = b[0] + b[1]*x

以下脚本行将绘制回归线并在其上放置标签：

plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()

最后，我们需要定义 main() 函数来提供数据集并调用我们上面定义的函数：

def main():
   x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
   y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
   b = coef_estimation(x, y)
   print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
   plot_regression_line(x, y, b)
   
if __name__ == "__main__":
main()

输出

Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788

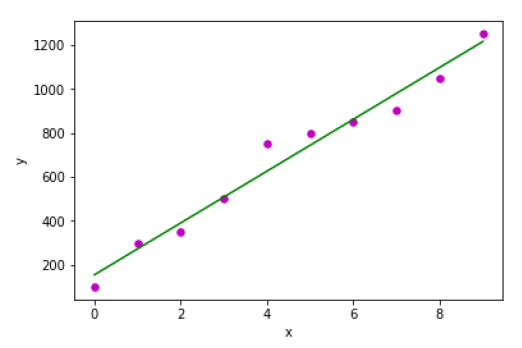
示例 2 - 在下面的 Python 实现示例中，我们使用 scikit-learn 的糖尿病数据集。

首先，我们将从导入必要的包开始：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

接下来，我们将加载糖尿病数据集并创建其对象：

diabetes = datasets.load_diabetes()

由于我们正在实现 SLR，我们将只使用一个特征：

X = diabetes.data[:, np.newaxis, 2]

接下来，我们需要将数据分割成训练集和测试集：

X_train = X[:-30]
X_test = X[-30:]

接下来，我们需要将目标分割成训练集和测试集：

y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]

现在，要训练模型，我们需要创建一个线性回归对象：

regr = linear_model.LinearRegression()

接下来，使用训练集训练模型：

regr.fit(X_train, y_train)

接下来，使用测试集进行预测：

y_pred = regr.predict(X_test)

接下来，我们将打印一些系数，例如 MSE、方差分数等：

print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))

现在，绘制输出：

plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

输出

Coefficients:
   [941.43097333]
Mean squared error: 3035.06
Variance score: 0.41

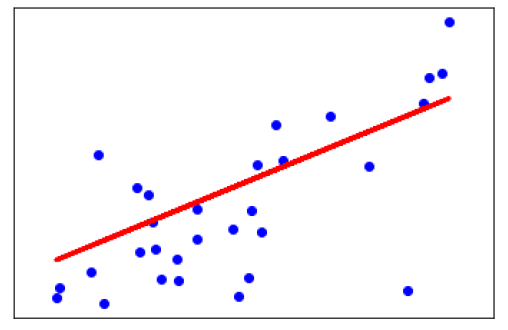
多元线性回归 (MLR)

它是简单线性回归的扩展，它使用两个或多个特征来预测响应。数学上我们可以解释如下：

考虑一个具有 n 个观察值、p 个特征（即自变量）和 y 作为单个响应（即因变量）的数据集，p 个特征的回归线可以计算如下：

$$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}$$

这里，h(x_i) 是预测的响应值，b₀,b₁,b₂…,b_p 是回归系数。

多元线性回归模型总是包含数据中的误差，称为残差误差，这会改变计算结果：

$$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}+e_{i}$$

我们也可以将上述等式写成：

$$y_{i}=h(x_{i})+e_{i}\:or\:e_{i}= y_{i} - h(x_{i})$$

Python 实现

在这个示例中，我们将使用 scikit-learn 的波士顿房价数据集：

首先，我们将从导入必要的包开始：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics

接下来，加载数据集：

boston = datasets.load_boston(return_X_y=False)

以下脚本行将定义特征矩阵 X 和响应向量 Y：

X = boston.data
y = boston.target

接下来，将数据集分割成训练集和测试集：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)

示例

现在，创建线性回归对象并训练模型：

reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
   color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
   color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()

输出

Coefficients:
[
   -1.16358797e-01  6.44549228e-02  1.65416147e-01  1.45101654e+00
   -1.77862563e+01  2.80392779e+00  4.61905315e-02 -1.13518865e+00
    3.31725870e-01 -1.01196059e-02 -9.94812678e-01  9.18522056e-03
   -7.92395217e-01
]
Variance score: 0.709454060230326

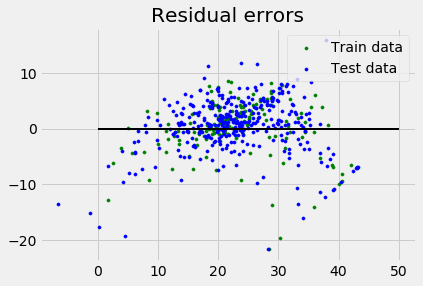
假设

以下是线性回归模型对数据集的一些假设：

多重共线性 - 线性回归模型假设数据中几乎没有或没有多重共线性。基本上，当自变量或特征之间存在依赖关系时，就会发生多重共线性。

自相关 - 线性回归模型的另一个假设是数据中几乎没有或没有自相关。基本上，当残差误差之间存在依赖关系时，就会发生自相关。

变量之间的关系 - 线性回归模型假设响应变量和特征变量之间的关系必须是线性的。