
- Python机器学习
- 首页
- 基础
- Python 生态系统
- 机器学习方法
- 机器学习项目的数据加载
- 用统计学理解数据
- 用可视化理解数据
- 数据准备
- 数据特征选择
- 机器学习算法 - 分类
- 介绍
- 逻辑回归
- 支持向量机 (SVM)
- 决策树
- 朴素贝叶斯
- 随机森林
- 机器学习算法 - 回归
- 随机森林
- 线性回归
- 机器学习算法 - 聚类
- 概述
- K均值算法
- 均值漂移算法
- 层次聚类
- 机器学习算法 - KNN算法
- 寻找最近邻
- 性能指标
- 自动化工作流
- 改进机器学习模型的性能
- 改进机器学习模型的性能(续…)
- Python机器学习 - 资源
- Python机器学习快速指南
- Python机器学习 - 资源
- Python机器学习 - 讨论
Python机器学习快速指南
Python机器学习 - 基础
我们正生活在“数据时代”,这个时代拥有更强大的计算能力和更多的存储资源。这些数据或信息日益增长,但真正的挑战在于如何理解所有这些数据。企业和组织正试图通过利用数据科学、数据挖掘和机器学习的概念和方法构建智能系统来应对这一挑战。其中,机器学习是计算机科学中最令人兴奋的领域之一。如果我们称机器学习为提供数据意义的算法的应用和科学,那也并不为过。
什么是机器学习?
机器学习 (ML) 是计算机科学的一个领域,借助它,计算机系统可以像人类一样理解数据。
简单来说,ML 是一种人工智能,它通过使用算法或方法从原始数据中提取模式。ML 的主要目标是让计算机系统从经验中学习,而无需明确的编程或人工干预。
机器学习的必要性
目前,人类是地球上最聪明、最先进的物种,因为他们能够思考、评估和解决复杂问题。另一方面,人工智能仍处于起步阶段,在许多方面尚未超越人类智能。那么问题是,为什么要让机器学习呢?最合适的理由是,“基于数据,高效且大规模地做出决策”。
最近,组织正在大量投资于人工智能、机器学习和深度学习等新技术,以获取数据中的关键信息,执行各种现实世界的任务和解决问题。我们可以称之为机器做出的数据驱动决策,特别是自动化流程。这些数据驱动决策可以用于解决那些无法通过编程逻辑固有解决的问题,而不是使用编程逻辑。事实是我们离不开人类智能,但另一方面,我们都需要高效且大规模地解决现实世界中的问题。这就是机器学习需求产生的原因。
为什么以及何时让机器学习?
我们已经讨论了机器学习的必要性,但另一个问题随之而来,在哪些情况下我们必须让机器学习?在许多情况下,我们需要机器高效且大规模地做出数据驱动决策。以下是一些让机器学习更有效的情况:
缺乏人类专业知识
我们希望机器学习并做出数据驱动决策的第一个场景可能是缺乏人类专业知识的领域。例如,在未知区域或太空行星中导航。
动态场景
有些场景本质上是动态的,即它们会随着时间推移而不断变化。对于这些场景和行为,我们希望机器学习并做出数据驱动决策。例如,组织中的网络连接和基础设施可用性。
难以将专业知识转化为计算任务
在许多领域,人类都拥有自己的专业知识,但他们无法将这些专业知识转化为计算任务。在这种情况下,我们需要机器学习。例如,语音识别、认知任务等领域。
机器学习模型
在讨论机器学习模型之前,我们需要理解米切尔教授给出的以下关于ML的正式定义:
“如果一个计算机程序在某些任务类别 T 中的性能,由性能度量 P 来衡量,随着经验 E 的积累而提高,则称该计算机程序从经验 E 中学习关于任务类别 T 的知识。”
上述定义主要关注三个参数,也是任何学习算法的主要组成部分,即任务 (T)、性能 (P) 和经验 (E)。在这种情况下,我们可以将此定义简化为:
ML 是人工智能的一个领域,它包含以下学习算法:
提高它们的性能 (P)
在执行某些任务 (T) 方面
随着时间的推移,积累经验 (E)
基于以上内容,下图表示机器学习模型:

现在让我们更详细地讨论它们:
任务 (T)
从问题的角度来看,我们可以将任务 T 定义为要解决的现实世界问题。这个问题可以是任何事情,例如在特定位置找到最佳房屋价格或找到最佳营销策略等。另一方面,如果我们谈论机器学习,任务的定义是不同的,因为很难通过传统的编程方法来解决基于ML的任务。
当任务 T 基于流程并且系统必须遵循的操作数据点时,则称其为基于ML的任务。基于ML的任务示例包括分类、回归、结构化标注、聚类、转录等。
经验 (E)
顾名思义,它是从提供给算法或模型的数据点中获得的知识。一旦提供了数据集,模型将迭代运行并学习一些内在模式。由此获得的学习称为经验 (E)。以人类学习为例,我们可以将其视为人类从各种属性(如情况、关系等)中学习或获得经验的情况。监督学习、无监督学习和强化学习是学习或获得经验的一些方法。我们的ML模型或算法获得的经验将用于解决任务 T。
性能 (P)
ML算法应该随着时间的推移执行任务并积累经验。衡量ML算法是否按预期执行的指标是其性能 (P)。P 本质上是一个定量指标,它说明模型如何使用其经验 E 来执行任务 T。有很多指标可以帮助理解ML性能,例如准确率得分、F1得分、混淆矩阵、精确率、召回率、灵敏度等。
机器学习的挑战
虽然机器学习正在快速发展,并在网络安全和自动驾驶汽车方面取得重大进步,但作为整体的人工智能领域仍有很长的路要走。其原因在于ML尚未克服许多挑战。ML目前面临的挑战包括:
数据质量 - 为ML算法提供高质量的数据是最大的挑战之一。使用低质量数据会导致与数据预处理和特征提取相关的问题。
耗时的任务 - ML模型面临的另一个挑战是耗费时间,尤其是在数据采集、特征提取和检索方面。
缺乏专业人员 - 由于ML技术仍处于起步阶段,因此获得专家资源是一项艰巨的任务。
缺乏明确的业务问题制定目标 - 缺乏明确的目标和明确定义的业务问题目标是ML面临的另一个关键挑战,因为这项技术尚未成熟。
过拟合和欠拟合问题 - 如果模型过拟合或欠拟合,则无法很好地表示该问题。
维度灾难 - ML模型面临的另一个挑战是数据点具有过多的特征。这可能是一个真正的障碍。
部署困难 - ML模型的复杂性使其难以在现实生活中部署。
机器学习的应用
机器学习是发展最快的技术之一,根据研究人员的说法,我们正处于人工智能和ML的黄金时代。它用于解决许多传统方法无法解决的现实世界中的复杂问题。以下是ML的一些现实世界应用:
情感分析
情绪分析
错误检测和预防
天气预报和预测
股票市场分析和预测
语音合成
语音识别
客户细分
物体识别
欺诈检测
欺诈预防
在网上购物中向客户推荐产品。
Python机器学习 - 生态系统
Python简介
Python 是一种流行的面向对象编程语言,具有高级编程语言的功能。它易于学习的语法和可移植性使其在如今广受欢迎。以下事实向我们介绍了 Python:
Python 由荷兰 Stichting Mathematisch Centrum 的 Guido van Rossum 开发。
它被编写为名为“ABC”的编程语言的后继者。
它的第一个版本于 1991 年发布。
Guido van Rossum 从名为 Monty Python's Flying Circus 的电视节目中选择了 Python 这个名字。
它是一种开源编程语言,这意味着我们可以免费下载它并使用它来开发程序。它可以从 www.python.org下载。
Python 编程语言兼具 Java 和 C 的特性。它拥有优雅的“C”代码,另一方面,它像 Java 一样拥有用于面向对象编程的类和对象。
它是一种解释型语言,这意味着 Python 程序的源代码将首先被转换为字节码,然后由 Python 虚拟机执行。
Python 的优缺点
每种编程语言都有其优点和缺点,Python 也不例外。
优点
根据研究和调查,Python 是第五重要的语言,也是机器学习和数据科学中最流行的语言。这是因为 Python 具有以下优点:
易于学习和理解 - Python 的语法更简单,因此即使是初学者也很容易学习和理解这门语言。
多用途语言 - Python 是一种多用途编程语言,因为它支持结构化编程、面向对象编程以及函数式编程。
大量的模块 - Python 拥有大量模块,涵盖了编程的各个方面。这些模块易于使用,因此 Python 成为一种可扩展的语言。
开源社区的支持 - 作为开源编程语言,Python 受到了非常庞大的开发者社区的支持。因此,Python 社区可以轻松修复 bug。此特性使 Python 非常强大且适应性强。
可扩展性 - Python 是一种可扩展的编程语言,因为它提供了一种比 shell 脚本更完善的结构来支持大型程序。
缺点
尽管 Python 是一种流行且强大的编程语言,但它也存在执行速度慢的缺点。
与编译型语言相比,Python 的执行速度较慢,因为 Python 是一种解释型语言。这可能是 Python 社区改进的主要方向。
安装 Python
要使用 Python,我们首先必须安装它。您可以通过以下两种方式之一安装 Python:
单独安装 Python
使用预打包的 Python 发行版 - Anaconda
让我们详细讨论一下这些方法。
单独安装 Python
如果要在您的计算机上安装 Python,则只需要下载适用于您平台的二进制代码即可。Python 发行版适用于 Windows、Linux 和 Mac 平台。
以下是上述平台上安装 Python 的快速概述:
在 Unix 和 Linux 平台上
借助以下步骤,我们可以在 Unix 和 Linux 平台上安装 Python:
接下来,点击链接下载适用于 Unix/Linux 的压缩源代码。
现在,下载并解压文件。
接下来,如果要自定义某些选项,可以编辑 Modules/Setup 文件。
接下来,运行命令 ./configure 脚本
make
make install
在 Windows 平台上
借助以下步骤,我们可以在 Windows 平台上安装 Python:
接下来,点击 Windows 安装程序 python-XYZ.msi 文件的链接。这里的 XYZ 是我们想要安装的版本。
现在,我们必须运行下载的文件。它将带我们进入 Python 安装向导,该向导易于使用。现在,接受默认设置并等待安装完成。
在 Macintosh 平台上
对于 Mac OS X,建议使用 Homebrew(一个很棒且易于使用的软件包安装程序)来安装 Python 3。如果您没有 Homebrew,可以使用以下命令安装它:
$ ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"
可以使用以下命令更新它:
$ brew update
现在,要在系统上安装 Python3,我们需要运行以下命令:
$ brew install python3
使用预打包的 Python 发行版:Anaconda
Anaconda 是 Python 的打包编译版本,其中包含数据科学中广泛使用的所有库。我们可以按照以下步骤使用 Anaconda 设置 Python 环境:
步骤 1 - 首先,我们需要从 Anaconda 发行版下载所需的安装包。链接为 https://anaconda.net.cn/distribution/。您可以根据需要选择 Windows、Mac 和 Linux 操作系统。
步骤 2 - 接下来,选择要在机器上安装的 Python 版本。最新的 Python 版本是 3.7。您将获得 64 位和 32 位图形安装程序的选项。
步骤 3 - 选择操作系统和 Python 版本后,它将下载 Anaconda 安装程序到您的计算机上。现在,双击该文件,安装程序将安装 Anaconda 包。
步骤 4 - 要检查它是否已安装,请打开命令提示符并键入 Python,如下所示:

您还可以观看以下详细的视频讲座:https://tutorialspoint.com/python_essentials_online_training/getting_started_with_anaconda.asp。
为什么选择 Python 用于数据科学?
Python 是第五大最重要的语言,也是机器学习和数据科学中最流行的语言。以下是一些使 Python 成为数据科学首选语言的功能:
丰富的软件包集
Python 拥有一个广泛而强大的软件包集,可用于各个领域。它还拥有 numpy、scipy、pandas、scikit-learn 等机器学习和数据科学所需的软件包。
易于原型设计
Python 的另一个重要特性是易于快速原型设计,这使得它成为数据科学的首选语言。此功能有助于开发新算法。
协作功能
数据科学领域基本上需要良好的协作,而 Python 提供了许多有用的工具,使协作变得极其简单。
一门语言,多个领域
典型的数据科学项目包含数据提取、数据处理、数据分析、特征提取、建模、评估、部署和更新解决方案等各个领域。由于 Python 是一种多用途语言,它允许数据科学家从一个通用平台解决所有这些领域的问题。
Python ML 生态系统的组件
在本节中,让我们讨论一些构成 Python 机器学习生态系统组件的核心数据科学库。这些有用的组件使 Python 成为一门重要的数据科学语言。尽管有许多这样的组件,但让我们在此处讨论一些 Python 生态系统的重要组件:
Jupyter Notebook
Jupyter Notebook 主要为开发基于 Python 的数据科学应用程序提供了一个交互式计算环境。它们以前被称为 ipython notebook。以下是一些使 Jupyter Notebook 成为 Python ML 生态系统最佳组件之一的功能:
Jupyter Notebook 可以通过以逐步的方式排列代码、图像、文本、输出等内容,逐步说明分析过程。
它有助于数据科学家在开发分析过程时记录思维过程。
还可以将结果作为笔记本的一部分捕获。
借助 Jupyter Notebook,我们还可以与同行共享我们的工作。
安装和执行
如果您使用的是 Anaconda 发行版,则无需单独安装 Jupyter Notebook,因为它已随发行版一起安装。您只需要转到 Anaconda Prompt 并键入以下命令:
C:\>jupyter notebook
按 Enter 键后,它将在计算机的 localhost:8888 上启动一个笔记本服务器。如下面的屏幕截图所示:

现在,点击“新建”选项卡后,您将获得一系列选项。选择 Python 3,它将带您进入新的笔记本,以便开始在其中工作。您将在以下屏幕截图中看到它的概览:
另一方面,如果您使用的是标准 Python 发行版,则可以使用流行的 Python 软件包安装程序 pip 安装 Jupyter Notebook。
pip install jupyter
Jupyter Notebook 中的单元格类型
Jupyter Notebook 中有三种类型的单元格:
代码单元格 - 顾名思义,我们可以使用这些单元格编写代码。编写代码/内容后,它会将其发送到与笔记本关联的内核。
Markdown 单元格 - 我们可以使用这些单元格记录计算过程。它们可以包含文本、图像、Latex 公式、HTML 标签等内容。
原始单元格 - 其中编写的文本按原样显示。这些单元格主要用于添加我们不希望 Jupyter Notebook 的自动转换机制进行转换的文本。
要更详细地学习 Jupyter Notebook,您可以访问以下链接:https://tutorialspoint.com/jupyter/index.htm。
NumPy
它是另一个有用的组件,使 Python 成为数据科学中最受欢迎的语言之一。它基本上代表 Numerical Python,包含多维数组对象。通过使用 NumPy,我们可以执行以下重要操作:
数组上的数学和逻辑运算。
傅里叶变换
与线性代数相关的运算。
我们还可以将 NumPy 视为 MatLab 的替代品,因为 NumPy 通常与 Scipy(科学 Python)和 Mat-plotlib(绘图库)一起使用。
安装和执行
如果您使用的是 Anaconda 发行版,则无需单独安装 NumPy,因为它已随发行版一起安装。您只需要使用以下方法将软件包导入 Python 脚本:
import numpy as np
另一方面,如果您使用的是标准 Python 发行版,则可以使用流行的 Python 软件包安装程序 pip 安装 NumPy。
pip install NumPy
要更详细地学习 NumPy,您可以访问以下链接: https://tutorialspoint.com/numpy/index.htm。
Pandas
它是另一个有用的 Python 库,使 Python 成为数据科学中最受欢迎的语言之一。Pandas 主要用于数据处理、整理和分析。它由 Wes McKinney 于 2008 年开发。借助 Pandas,在数据处理中,我们可以完成以下五个步骤:
加载
准备
操作
建模
分析
Pandas 中的数据表示
Pandas 中的数据表示完全借助以下三种数据结构完成:
序列 - 它基本上是一个具有轴标签的一维 ndarray,这意味着它就像一个具有同类数据的简单数组。例如,以下序列是整数 1、5、10、15、24、25…的集合。
| 1 | 5 | 10 | 15 | 24 | 25 | 28 | 36 | 40 | 89 |
数据框 - 它是最有用的数据结构,用于 Pandas 中几乎所有类型的数据表示和操作。它基本上是一个二维数据结构,可以包含异类数据。通常,表格数据使用数据框表示。例如,下表显示了学生的姓名、学号、年龄和性别数据:
姓名 |
学号 |
年龄 |
性别 |
|---|---|---|---|
Aarav |
1 |
15 |
男 |
Harshit |
2 |
14 |
男 |
Kanika |
3 |
16 |
女 |
Mayank |
4 |
15 |
男 |
面板 - 它是一个包含异类数据的 3 维数据结构。用图形表示面板非常困难,但可以将其说明为 DataFrame 的容器。
下表提供了有关 Pandas 中使用的上述数据结构的维度和描述:
数据结构 |
维度 |
描述 |
|---|---|---|
序列 |
1-D |
大小不可变,1-D 同类数据 |
数据框 |
2-D |
大小可变,表格形式的异类数据 |
面板 |
3-D |
大小可变的数组,DataFrame 的容器。 |
我们可以将这些数据结构理解为更高维的数据结构是较低维数据结构的容器。
安装和执行
如果您使用的是 Anaconda 发行版,则无需单独安装 Pandas,因为它已随发行版一起安装。您只需要使用以下方法将软件包导入 Python 脚本:
import pandas as pd
另一方面,如果您使用的是标准 Python 发行版,则可以使用流行的 Python 软件包安装程序 pip 安装 Pandas。
pip install Pandas
安装 Pandas 后,您可以将其导入 Python 脚本,如上所述。
示例
以下是使用 Pandas 从 ndarray 创建序列的示例:
In [1]: import pandas as pd In [2]: import numpy as np In [3]: data = np.array(['g','a','u','r','a','v']) In [4]: s = pd.Series(data) In [5]: print (s) 0 g 1 a 2 u 3 r 4 a 5 v dtype: object
要更详细地学习 Pandas,您可以访问以下链接:https://tutorialspoint.com/python_pandas/index.htm。
Scikit-learn
另一个有用且最重要的 Python 数据科学和机器学习库是 Scikit-learn。以下是一些使 Scikit-learn 如此有用的特性:
它建立在 NumPy、SciPy 和 Matplotlib 之上。
它是开源的,可以在 BSD 许可下重用。
每个人都可以访问它,并且可以在各种环境中重用。
借助它,可以实现涵盖机器学习主要领域的多种机器学习算法,例如分类、聚类、回归、降维、模型选择等。
安装和执行
如果您使用的是Anaconda发行版,则无需单独安装Scikit-learn,因为它已经随Anaconda一起安装。您只需要在Python脚本中使用该包即可。例如,使用以下脚本行,我们从Scikit-learn导入乳腺癌患者的数据集:
from sklearn.datasets import load_breast_cancer
另一方面,如果您使用的是标准Python发行版并且拥有NumPy和SciPy,则可以使用流行的Python包安装程序pip安装Scikit-learn。
pip install -U scikit-learn
安装Scikit-learn后,您可以像上面所做的那样在Python脚本中使用它。
Python机器学习 - 方法
有多种机器学习算法、技术和方法可用于构建模型,通过使用数据解决现实生活中的问题。在本章中,我们将讨论这些不同类型的方法。
不同类型的方法
以下是基于一些广泛类别的各种机器学习方法:
基于人工监督
在学习过程中,一些基于人工监督的方法如下:
监督学习
监督学习算法或方法是最常用的机器学习算法。此方法或学习算法在训练过程中获取数据样本(即训练数据)及其关联的输出(即标签或响应),每个数据样本都带有相应的输出。
监督学习算法的主要目标是在执行多个训练数据实例后,学习输入数据样本和相应输出之间的关联。
例如,我们有
x:输入变量和
Y:输出变量
现在,应用算法学习从输入到输出的映射函数,如下所示:
Y=f(x)
现在,主要目标将是很好地逼近映射函数,以便即使当我们有新的输入数据(x)时,我们也可以轻松地预测该新输入数据的输出变量(Y)。
之所以称为监督学习,是因为整个学习过程可以被认为是在老师或监督者的监督下进行的。监督机器学习算法的示例包括决策树、随机森林、KNN、逻辑回归等。
基于机器学习任务,监督学习算法可以分为以下两大类:
分类
回归
分类
基于分类的任务的关键目标是针对给定的输入数据预测类别输出标签或响应。输出将基于模型在训练阶段学到的内容。众所周知,类别输出响应意味着无序和离散值,因此每个输出响应都属于特定的类或类别。我们还将在后续章节中详细讨论分类和相关算法。
回归
基于回归的任务的关键目标是针对给定的输入数据预测输出标签或响应,这些标签或响应是连续的数值。输出将基于模型在训练阶段学到的内容。基本上,回归模型使用输入数据特征(自变量)及其相应的连续数值输出值(因变量或结果变量)来学习输入和相应输出之间的特定关联。我们还将在后续章节中详细讨论回归和相关算法。
无监督学习
顾名思义,它与监督机器学习方法或算法相反,这意味着在无监督机器学习算法中,我们没有任何监督者提供任何形式的指导。在没有像监督学习算法那样拥有预先标记的训练数据的自由,并且我们想要从输入数据中提取有用模式的情况下,无监督学习算法非常实用。
例如,可以理解为:
假设我们有:
x:输入变量,那么将没有相应的输出变量,算法需要发现数据中的有趣模式以进行学习。
无监督机器学习算法的示例包括K均值聚类、K最近邻等。
基于机器学习任务,无监督学习算法可以分为以下广泛类别:
聚类
关联
降维
聚类
聚类方法是最有用的无监督机器学习方法之一。这些算法用于查找数据样本之间的相似性和关系模式,然后根据特征将这些样本聚类到具有相似性的组中。聚类的现实世界示例是根据客户的购买行为对客户进行分组。
关联
另一种有用的无监督机器学习方法是关联,它用于分析大型数据集以查找模式,这些模式进一步表示各种项目之间有趣的关系。它也称为关联规则挖掘或市场篮分析,主要用于分析客户的购物模式。
降维
此无监督机器学习方法用于通过选择一组主要或代表性特征来减少每个数据样本的特征变量数量。这里出现了一个问题,那就是为什么我们需要降低维度?其背后的原因是特征空间复杂性问题,当我们开始从数据样本中分析和提取数百万个特征时,就会出现这种问题。此问题通常称为“维数灾难”。PCA(主成分分析)、K最近邻和判别分析是用于此目的的一些流行算法。
异常检测
此无监督机器学习方法用于找出通常不会发生的罕见事件或观察结果的发生情况。通过使用学习到的知识,异常检测方法能够区分异常数据点或正常数据点。一些无监督算法(如聚类、KNN)可以根据数据及其特征检测异常。
半监督学习
此类算法或方法既不是完全监督的,也不是完全无监督的。它们基本上介于两者之间,即监督学习方法和无监督学习方法。这些类型的算法通常使用少量监督学习组件(即少量预先标记的注释数据)和大量无监督学习组件(即大量未标记数据)进行训练。我们可以遵循以下任何一种方法来实现半监督学习方法:
第一种简单的方法是基于少量标记和注释数据构建监督模型,然后通过将其应用于大量未标记数据来构建无监督模型以获得更多标记样本。现在,在它们上训练模型并重复此过程。
- ,p>第二种方法需要一些额外的努力。在这种方法中,我们可以首先使用无监督方法对相似的数据样本进行聚类,注释这些组,然后使用此信息的组合来训练模型。
强化学习
这些方法不同于之前研究的方法,而且很少使用。在这种类型的学习算法中,将有一个代理,我们希望对其进行一段时间训练,以便它可以与特定环境交互。代理将遵循一组与环境交互的策略,然后在观察环境后,它将根据环境的当前状态采取行动。强化学习方法的主要步骤如下:
步骤1 - 首先,我们需要为代理准备一些初始策略集。
步骤2 - 然后观察环境及其当前状态。
步骤3 - 接下来,根据环境的当前状态选择最佳策略并执行重要操作。
步骤4 - 现在,代理可以根据其在上一步骤中采取的操作获得相应的奖励或惩罚。
步骤5 - 现在,如果需要,我们可以更新策略。
步骤6 - 最后,重复步骤 2-5,直到代理学会并采用最佳策略。
适合机器学习的任务
下图显示了哪种类型的任务适合各种机器学习问题:

基于学习能力
在学习过程中,以下是一些基于学习能力的方法:
批量学习
在许多情况下,我们有端到端的机器学习系统,我们需要使用所有可用的训练数据一次性训练模型。这种类型的学习方法或算法称为批量学习或离线学习。之所以称为批量学习或离线学习,是因为它是一个一次性过程,模型将使用数据在一个批次中进行训练。以下是批量学习方法的主要步骤:
步骤1 - 首先,我们需要收集所有训练数据以开始训练模型。
步骤2 - 现在,通过一次性提供所有训练数据来开始模型的训练。
步骤3 - 接下来,一旦获得令人满意的结果/性能,就停止学习/训练过程。
步骤4 - 最后,将此训练后的模型部署到生产环境中。在这里,它将预测新数据样本的输出。
在线学习
它与批量学习或离线学习方法完全相反。在这些学习方法中,训练数据以多个增量批次(称为小批量)提供给算法。以下是在线学习方法的主要步骤:
步骤1 - 首先,我们需要收集所有训练数据以开始训练模型。
步骤2 - 现在,通过向算法提供训练数据的小批量来开始模型的训练。
步骤3 - 接下来,我们需要以多个增量向算法提供训练数据的小批量。
步骤4 - 因为它不会像批量学习那样停止,因此在以小批量提供所有训练数据后,还会向其提供新的数据样本。
步骤5 - 最后,它将根据新的数据样本持续学习一段时间。
基于泛化方法
在学习过程中,以下是一些基于泛化方法的方法:
基于实例的学习
基于实例的学习方法是一种有用的方法,它通过基于输入数据进行泛化来构建机器学习模型。它与之前研究的学习方法相反,因为这种类型的学习涉及机器学习系统以及使用原始数据点本身来为较新的数据样本绘制结果的方法,而无需在训练数据上构建显式模型。
简单来说,基于实例的学习基本上从查看输入数据点开始,然后使用相似性度量,它将泛化并预测新的数据点。
基于模型的学习
在基于模型的学习方法中,一个迭代过程发生在基于各种模型参数(称为超参数)构建的机器学习模型上,其中使用输入数据来提取特征。在这种学习中,超参数是根据各种模型验证技术进行优化的。这就是为什么我们可以说基于模型的学习方法对泛化使用了更传统的机器学习方法。
机器学习项目的数据加载
假设您想启动一个机器学习项目,那么您首先需要什么最重要的事情?它是我们启动任何机器学习项目都需要加载的数据。关于数据,机器学习项目中最常见的格式是 CSV(逗号分隔值)。
基本上,CSV 是一种简单的文件格式,用于以纯文本格式存储表格数据(数字和文本),例如电子表格。在 Python 中,我们可以通过不同的方式将 CSV 数据加载到中,但在加载 CSV 数据之前,我们必须注意一些事项。
加载 CSV 数据时的注意事项
CSV 数据格式是机器学习数据中最常见的格式,但在将其加载到我们的机器学习项目中时,我们需要注意以下主要事项:
文件头
在 CSV 数据文件中,文件头包含每个字段的信息。我们必须对文件头和数据文件使用相同的定界符,因为文件头指定了如何解释数据字段。
以下是必须考虑的与 CSV 文件头相关的两种情况:
情况一:当数据文件具有文件头时 - 如果数据文件具有文件头,它将自动为数据的每一列分配名称。
情况二:当数据文件没有文件头时 - 如果数据文件没有文件头,我们需要手动为数据的每一列分配名称。
在这两种情况下,我们都需要明确指定我们的 CSV 文件是否包含文件头。
注释
任何数据文件中的注释都具有其重要性。在 CSV 数据文件中,注释由行首的哈希符号 (#) 表示。在将 CSV 数据加载到机器学习项目中时,我们需要考虑注释,因为如果我们在文件中包含注释,则可能需要指示(取决于我们选择的加载方法)是否期望这些注释。
分隔符
在 CSV 数据文件中,逗号 (,) 字符是标准分隔符。分隔符的作用是分隔字段中的值。在将 CSV 文件上传到机器学习项目时,考虑分隔符的作用非常重要,因为我们也可以使用其他分隔符,例如制表符或空格。但是,如果使用与标准分隔符不同的分隔符,则必须明确指定它。
引号
在 CSV 数据文件中,双引号 (“ ”) 标记是默认的引号字符。在将 CSV 文件上传到机器学习项目时,考虑引号的作用非常重要,因为我们也可以使用双引号标记以外的其他引号字符。但是,如果使用与标准引号字符不同的引号字符,则必须明确指定它。
加载 CSV 数据文件的方法
在使用机器学习项目时,最关键的任务是将数据正确地加载到其中。机器学习项目中最常见的数据格式是 CSV,它有多种形式,并且解析难度各不相同。在本节中,我们将讨论在 Python 中加载 CSV 数据文件的三种常见方法:
使用 Python 标准库加载 CSV
加载 CSV 数据文件的第一种也是最常用的方法是使用 Python 标准库,它为我们提供了各种内置模块,即 csv 模块和 reader() 函数。以下是使用它加载 CSV 数据文件的示例:
示例
在这个示例中,我们使用的是鸢尾花数据集,可以将其下载到我们的本地目录中。加载数据文件后,我们可以将其转换为 NumPy 数组,并在机器学习项目中使用它。以下是加载 CSV 数据文件的 Python 脚本:
首先,我们需要导入 Python 标准库提供的 csv 模块,如下所示:
import csv
接下来,我们需要导入 Numpy 模块,以便将加载的数据转换为 NumPy 数组。
import numpy as np
现在,提供存储在我们本地目录中的包含 CSV 数据文件的文件的完整路径:
path = r"c:\iris.csv"
接下来,使用 csv.reader() 函数从 CSV 文件读取数据:
with open(path,'r') as f: reader = csv.reader(f,delimiter = ',') headers = next(reader) data = list(reader) data = np.array(data).astype(float)
我们可以使用以下脚本行打印标题的名称:
print(headers)
以下脚本行将打印数据的形状,即文件中的行数和列数:
print(data.shape)
下一个脚本行将给出数据文件的前三行:
print(data[:3])
输出
['sepal_length', 'sepal_width', 'petal_length', 'petal_width'] (150, 4) [ [5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2]]
使用 NumPy 加载 CSV
加载 CSV 数据文件的另一种方法是 NumPy 和 numpy.loadtxt() 函数。以下是使用它加载 CSV 数据文件的示例:
示例
在这个示例中,我们使用的是 Pima 印第安人数据集,其中包含糖尿病患者的数据。此数据集是一个没有标题的数字数据集。它也可以下载到我们的本地目录中。加载数据文件后,我们可以将其转换为 NumPy 数组,并在机器学习项目中使用它。以下是加载 CSV 数据文件的 Python 脚本:
from numpy import loadtxt path = r"C:\pima-indians-diabetes.csv" datapath= open(path, 'r') data = loadtxt(datapath, delimiter=",") print(data.shape) print(data[:3])
输出
(768, 9) [ [ 6. 148. 72. 35. 0. 33.6 0.627 50. 1.] [ 1. 85. 66. 29. 0. 26.6 0.351 31. 0.] [ 8. 183. 64. 0. 0. 23.3 0.672 32. 1.]]
使用 Pandas 加载 CSV
加载 CSV 数据文件的另一种方法是使用 Pandas 和 pandas.read_csv() 函数。这是一个非常灵活的函数,它返回一个 pandas.DataFrame,可以立即用于绘图。以下是使用它加载 CSV 数据文件的示例:
示例
在这里,我们将实现两个 Python 脚本,第一个是使用包含标题的鸢尾花数据集,另一个是使用 Pima 印第安人数据集,这是一个没有标题的数字数据集。这两个数据集都可以下载到本地目录中。
脚本 1
以下是使用 Pandas 在鸢尾花数据集上加载 CSV 数据文件的 Python 脚本:
from pandas import read_csv path = r"C:\iris.csv" data = read_csv(path) print(data.shape) print(data[:3]) Output: (150, 4) sepal_length sepal_width petal_length petal_width 0 5.1 3.5 1.4 0.2 1 4.9 3.0 1.4 0.2 2 4.7 3.2 1.3 0.2
脚本 2
以下是使用 Pandas 在 Pima 印第安人糖尿病数据集上加载 CSV 数据文件以及提供标题名称的 Python 脚本:
from pandas import read_csv path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) print(data.shape) print(data[:3])
输出
(768, 9) preg plas pres skin test mass pedi age class 0 6 148 72 35 0 33.6 0.627 50 1 1 1 85 66 29 0 26.6 0.351 31 0 2 8 183 64 0 0 23.3 0.672 32 1
通过给定的示例,可以很容易地理解上述三种加载 CSV 数据文件的方法之间的区别。
机器学习 - 使用统计数据理解数据
介绍
在使用机器学习项目时,我们通常会忽略两个最重要的部分,即数学和数据。这是因为,我们知道机器学习是一种数据驱动的方法,我们的机器学习模型产生的结果只会与我们提供给它的数据一样好或一样坏。
在上一章中,我们讨论了如何将 CSV 数据上传到我们的机器学习项目中,但在上传之前了解数据会更好。我们可以通过两种方式理解数据,即使用统计数据和使用可视化。
在本章中,我们将借助以下 Python 代码示例,使用统计数据来理解机器学习数据。
查看原始数据
第一个代码示例用于查看原始数据。查看原始数据很重要,因为在查看原始数据后获得的见解将提高我们更好地预处理以及处理机器学习项目数据的几率。
以下是使用 Pandas DataFrame 的 head() 函数在 Pima 印第安人糖尿病数据集上实现的 Python 脚本,用于查看前 50 行以更好地理解它:
示例
from pandas import read_csv path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) print(data.head(50))
输出
preg plas pres skin test mass pedi age class 0 6 148 72 35 0 33.6 0.627 50 1 1 1 85 66 29 0 26.6 0.351 31 0 2 8 183 64 0 0 23.3 0.672 32 1 3 1 89 66 23 94 28.1 0.167 21 0 4 0 137 40 35 168 43.1 2.288 33 1 5 5 116 74 0 0 25.6 0.201 30 0 6 3 78 50 32 88 31.0 0.248 26 1 7 10 115 0 0 0 35.3 0.134 29 0 8 2 197 70 45 543 30.5 0.158 53 1 9 8 125 96 0 0 0.0 0.232 54 1 10 4 110 92 0 0 37.6 0.191 30 0 11 10 168 74 0 0 38.0 0.537 34 1 12 10 139 80 0 0 27.1 1.441 57 0 13 1 189 60 23 846 30.1 0.398 59 1 14 5 166 72 19 175 25.8 0.587 51 1 15 7 100 0 0 0 30.0 0.484 32 1 16 0 118 84 47 230 45.8 0.551 31 1 17 7 107 74 0 0 29.6 0.254 31 1 18 1 103 30 38 83 43.3 0.183 33 0 19 1 115 70 30 96 34.6 0.529 32 1 20 3 126 88 41 235 39.3 0.704 27 0 21 8 99 84 0 0 35.4 0.388 50 0 22 7 196 90 0 0 39.8 0.451 41 1 23 9 119 80 35 0 29.0 0.263 29 1 24 11 143 94 33 146 36.6 0.254 51 1 25 10 125 70 26 115 31.1 0.205 41 1 26 7 147 76 0 0 39.4 0.257 43 1 27 1 97 66 15 140 23.2 0.487 22 0 28 13 145 82 19 110 22.2 0.245 57 0 29 5 117 92 0 0 34.1 0.337 38 0 30 5 109 75 26 0 36.0 0.546 60 0 31 3 158 76 36 245 31.6 0.851 28 1 32 3 88 58 11 54 24.8 0.267 22 0 33 6 92 92 0 0 19.9 0.188 28 0 34 10 122 78 31 0 27.6 0.512 45 0 35 4 103 60 33 192 24.0 0.966 33 0 36 11 138 76 0 0 33.2 0.420 35 0 37 9 102 76 37 0 32.9 0.665 46 1 38 2 90 68 42 0 38.2 0.503 27 1 39 4 111 72 47 207 37.1 1.390 56 1 40 3 180 64 25 70 34.0 0.271 26 0 41 7 133 84 0 0 40.2 0.696 37 0 42 7 106 92 18 0 22.7 0.235 48 0 43 9 171 110 24 240 45.4 0.721 54 1 44 7 159 64 0 0 27.4 0.294 40 0 45 0 180 66 39 0 42.0 1.893 25 1 46 1 146 56 0 0 29.7 0.564 29 0 47 2 71 70 27 0 28.0 0.586 22 0 48 7 103 66 32 0 39.1 0.344 31 1 49 7 105 0 0 0 0.0 0.305 24 0
从上面的输出中我们可以观察到,第一列给出了行号,这对于引用特定观察结果非常有用。
检查数据的维度
了解机器学习项目有多少数据(以行和列表示)始终是一个好习惯。其背后的原因是:
假设如果我们有太多行和列,那么运行算法和训练模型将需要很长时间。
假设如果我们有太少的行和列,那么我们将没有足够的数据来很好地训练模型。
以下是通过在 Pandas Data Frame 上打印 shape 属性实现的 Python 脚本。我们将对鸢尾花数据集实施它,以获取其中的总行数和列数。
示例
from pandas import read_csv path = r"C:\iris.csv" data = read_csv(path) print(data.shape)
输出
(150, 4)
我们可以很容易地从输出中观察到,我们将要使用的鸢尾花数据集有 150 行和 4 列。
获取每个属性的数据类型
了解每个属性的数据类型是另一个好习惯。其背后的原因是,根据需要,有时我们需要将一种数据类型转换为另一种数据类型。例如,我们可能需要将字符串转换为浮点数或整数,以表示类别或序数值。我们可以通过查看原始数据来了解属性的数据类型,但另一种方法是使用 Pandas DataFrame 的 dtypes 属性。借助 dtypes 属性,我们可以对每个属性的数据类型进行分类。这可以通过以下 Python 脚本了解:
示例
from pandas import read_csv path = r"C:\iris.csv" data = read_csv(path) print(data.dtypes)
输出
sepal_length float64 sepal_width float64 petal_length float64 petal_width float64 dtype: object
从上面的输出中,我们可以很容易地获取每个属性的数据类型。
数据的统计摘要
我们已经讨论了获取数据形状(即行数和列数)的 Python 代码示例,但很多时候我们需要查看该数据形状之外的摘要。这可以通过 Pandas DataFrame 的 describe() 函数来完成,该函数进一步提供每个数据属性的以下 8 个统计属性:
计数
平均值
标准差
最小值
最大值
25%
中位数,即 50%
75%
示例
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
print(data.shape)
print(data.describe())
输出
(768, 9)
preg plas pres skin test mass pedi age class
count 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00
mean 3.85 120.89 69.11 20.54 79.80 31.99 0.47 33.24 0.35
std 3.37 31.97 19.36 15.95 115.24 7.88 0.33 11.76 0.48
min 0.00 0.00 0.00 0.00 0.00 0.00 0.08 21.00 0.00
25% 1.00 99.00 62.00 0.00 0.00 27.30 0.24 24.00 0.00
50% 3.00 117.00 72.00 23.00 30.50 32.00 0.37 29.00 0.00
75% 6.00 140.25 80.00 32.00 127.25 36.60 0.63 41.00 1.00
max 17.00 199.00 122.00 99.00 846.00 67.10 2.42 81.00 1.00
从上面的输出中,我们可以观察到 Pima 印第安人糖尿病数据集的数据的统计摘要以及数据的形状。
查看类别分布
类别分布统计在分类问题中非常有用,在这些问题中我们需要了解类别值的平衡。了解类别值分布非常重要,因为如果我们具有高度不平衡的类别分布(即一个类别的观察值比其他类别多得多),那么在机器学习项目的预处理阶段可能需要特殊处理。我们可以轻松地借助 Pandas DataFrame 在 Python 中获取类别分布。
示例
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
count_class = data.groupby('class').size()
print(count_class)
输出
Class 0 500 1 268 dtype: int64
从上面的输出中可以清楚地看出,类别为 0 的观察值数量几乎是类别为 1 的观察值数量的两倍。
查看属性之间的相关性
两个变量之间的关系称为相关性。在统计学中,计算相关性的最常用方法是皮尔逊相关系数。它可以具有以下三个值:
系数值 = 1 - 它表示变量之间完全正相关。
系数值 = -1 - 它表示变量之间完全负相关。
系数值 = 0 - 它表示变量之间没有相关性。
在将数据集用于机器学习项目之前,审查其属性之间的两两相关性始终是一个好习惯,因为某些机器学习算法(例如线性回归和逻辑回归)在存在高度相关的属性时性能会很差。在 Python 中,我们可以借助 Pandas DataFrame 上的 corr() 函数轻松计算数据集属性的相关矩阵。
示例
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
correlations = data.corr(method='pearson')
print(correlations)
输出
preg plas pres skin test mass pedi age class preg 1.00 0.13 0.14 -0.08 -0.07 0.02 -0.03 0.54 0.22 plas 0.13 1.00 0.15 0.06 0.33 0.22 0.14 0.26 0.47 pres 0.14 0.15 1.00 0.21 0.09 0.28 0.04 0.24 0.07 skin -0.08 0.06 0.21 1.00 0.44 0.39 0.18 -0.11 0.07 test -0.07 0.33 0.09 0.44 1.00 0.20 0.19 -0.04 0.13 mass 0.02 0.22 0.28 0.39 0.20 1.00 0.14 0.04 0.29 pedi -0.03 0.14 0.04 0.18 0.19 0.14 1.00 0.03 0.17 age 0.54 0.26 0.24 -0.11 -0.04 0.04 0.03 1.00 0.24 class 0.22 0.47 0.07 0.07 0.13 0.29 0.17 0.24 1.00
以上输出中的矩阵给出了数据集中所有属性对之间的相关性。
审查属性分布的偏度
偏度可以定义为假定为高斯分布但出现扭曲或向一个方向或另一个方向偏移的分布,或者向左或向右偏移。审查属性的偏度是一项重要的任务,原因如下:
数据中存在偏度需要在数据准备阶段进行校正,以便我们能够从模型中获得更高的准确性。
大多数机器学习算法假设数据服从高斯分布,即正态分布或钟形曲线数据。
在 Python 中,我们可以使用 Pandas DataFrame 上的 skew() 函数轻松计算每个属性的偏度。
示例
from pandas import read_csv path = r"C:\pima-indians-diabetes.csv" names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=names) print(data.skew())
输出
preg 0.90 plas 0.17 pres -1.84 skin 0.11 test 2.27 mass -0.43 pedi 1.92 age 1.13 class 0.64 dtype: float64
从以上输出可以观察到正偏度或负偏度。如果值接近于零,则表示偏度较小。
机器学习 - 使用可视化理解数据
介绍
在上一章中,我们讨论了数据对于机器学习算法的重要性,以及一些用于使用统计方法理解数据的 Python 代码示例。还有一种方法称为可视化,可以用来理解数据。
借助数据可视化,我们可以看到数据的形态以及数据属性之间存在何种相关性。这是查看特征是否对应于输出的最快方法。借助以下 Python 代码示例,我们可以使用统计方法理解机器学习数据。

单变量图:独立理解属性
最简单的可视化类型是单变量或“单变量”可视化。借助单变量可视化,我们可以独立地理解数据集的每个属性。以下是使用 Python 实现单变量可视化的一些技术:
直方图
直方图将数据分组到若干区间中,是快速了解数据集中每个属性分布的最有效方法。以下是直方图的一些特征:
它为我们提供了每个用于可视化的区间中观测值的计数。
从区间的形状,我们可以轻松地观察分布,例如它是高斯分布、偏态分布还是指数分布。
直方图还有助于我们发现可能的异常值。
示例
以下显示的代码是创建皮马印第安人糖尿病数据集属性直方图的 Python 脚本示例。这里,我们将使用 Pandas DataFrame 上的 hist() 函数生成直方图,并使用matplotlib进行绘图。
from matplotlib import pyplot from pandas import read_csv path = r"C:\pima-indians-diabetes.csv" names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=names) data.hist() pyplot.show()
输出
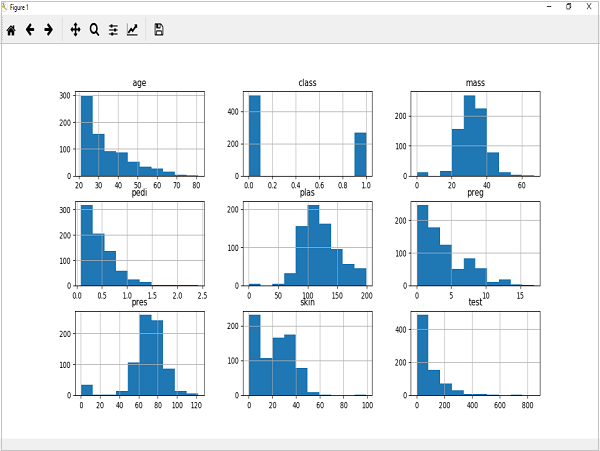
以上输出显示它为数据集中每个属性创建了直方图。由此,我们可以观察到,年龄、pedi 和 test 属性可能服从指数分布,而 mass 和 plas 属性可能服从高斯分布。
密度图
获取每个属性分布的另一种快速简便的技术是密度图。它也类似于直方图,但在每个区间的顶部绘制一条平滑的曲线。我们可以将它们称为抽象的直方图。
示例
在以下示例中,Python 脚本将生成皮马印第安人糖尿病数据集属性分布的密度图。
from matplotlib import pyplot from pandas import read_csv path = r"C:\pima-indians-diabetes.csv" names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=names) data.plot(kind='density', subplots=True, layout=(3,3), sharex=False) pyplot.show()
输出
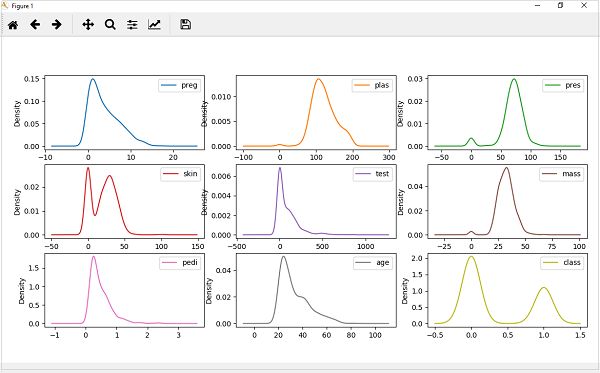
从以上输出可以轻松理解密度图和直方图之间的区别。
箱线图
箱线图,简称箱图,是另一种用于审查每个属性分布的有用技术。以下是此技术的一些特征:
它本质上是单变量的,并总结了每个属性的分布。
它为中间值(即中位数)绘制一条线。
它围绕 25% 和 75% 绘制一个框。
它还绘制了须线,这将使我们了解数据的扩展。
须线外部的点表示异常值。异常值将是中间数据扩展大小的 1.5 倍。
示例
在以下示例中,Python 脚本将生成皮马印第安人糖尿病数据集属性分布的密度图。
from matplotlib import pyplot from pandas import read_csv path = r"C:\pima-indians-diabetes.csv" names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=names) data.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False) pyplot.show()
输出
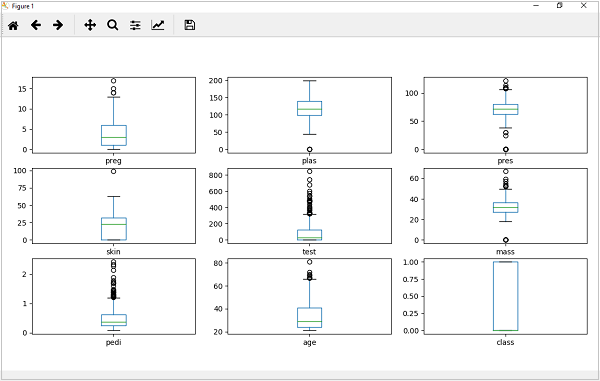
从以上属性分布图可以看出,年龄、test 和 skin 属性向较小值方向倾斜。
多变量图:多个变量之间的交互
另一种可视化类型是多变量或“多变量”可视化。借助多变量可视化,我们可以理解数据集多个属性之间的交互。以下是使用 Python 实现多变量可视化的一些技术:
相关矩阵图
相关性是关于两个变量之间变化的指示。在我们之前的章节中,我们已经讨论了皮尔逊相关系数以及相关性的重要性。我们可以绘制相关矩阵来显示哪个变量相对于另一个变量具有高相关性或低相关性。
示例
在以下示例中,Python 脚本将生成并绘制皮马印第安人糖尿病数据集的相关矩阵。它可以使用 Pandas DataFrame 上的 corr() 函数生成,并使用 pyplot 进行绘图。
from matplotlib import pyplot from pandas import read_csv import numpy Path = r"C:\pima-indians-diabetes.csv" names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(Path, names=names) correlations = data.corr() fig = pyplot.figure() ax = fig.add_subplot(111) cax = ax.matshow(correlations, vmin=-1, vmax=1) fig.colorbar(cax) ticks = numpy.arange(0,9,1) ax.set_xticks(ticks) ax.set_yticks(ticks) ax.set_xticklabels(names) ax.set_yticklabels(names) pyplot.show()
输出
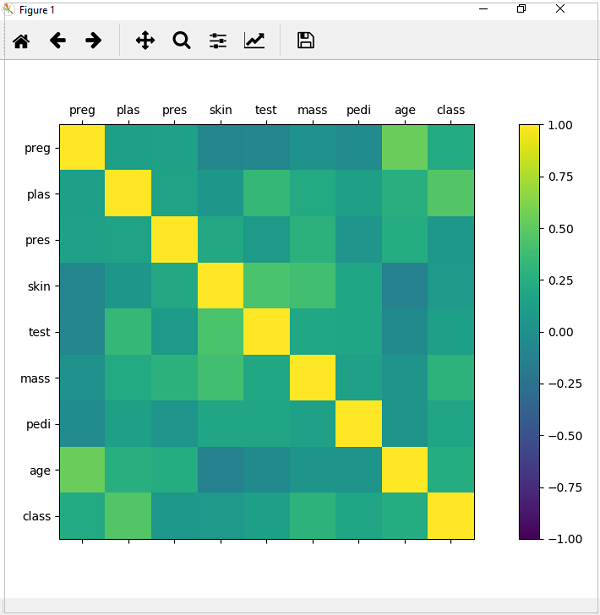
从以上相关矩阵输出可以看出,它是对称的,即左下角与右上角相同。还可以观察到每个变量彼此之间都呈正相关。
散点矩阵图
散点图使用二维空间中的点来显示一个变量受另一个变量影响的程度或它们之间的关系。从概念上讲,散点图非常类似于折线图,它们使用水平和垂直轴来绘制数据点。
示例
在以下示例中,Python 脚本将生成并绘制皮马印第安人糖尿病数据集的散点矩阵。它可以使用 Pandas DataFrame 上的 scatter_matrix() 函数生成,并使用 pyplot 进行绘图。
from matplotlib import pyplot from pandas import read_csv from pandas.tools.plotting import scatter_matrix path = r"C:\pima-indians-diabetes.csv" names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=names) scatter_matrix(data) pyplot.show()
输出

使用 Python 进行机器学习 - 数据准备
介绍
机器学习算法完全依赖于数据,因为它是使模型训练成为可能的至关重要的方面。另一方面,如果我们在将数据馈送到机器学习算法之前无法理解它,那么机器将毫无用处。简单来说,我们始终需要馈送正确的数据,即按正确比例、格式并包含有意义特征的数据,以解决我们希望机器解决的问题。
这使得数据准备成为机器学习过程中最重要的步骤。数据准备可以定义为使我们的数据集更适合机器学习过程的程序。
为什么要进行数据预处理?
在选择用于机器学习训练的原始数据后,最重要的任务是数据预处理。从广义上讲,数据预处理将把选择的数据转换为我们可以处理或可以馈送到机器学习算法的形式。我们始终需要预处理我们的数据,以便它能够满足机器学习算法的期望。
数据预处理技术
我们有以下数据预处理技术,可以应用于数据集以生成用于机器学习算法的数据:
缩放
我们的数据集很可能包含具有不同比例的属性,但我们不能将此类数据提供给机器学习算法,因此需要进行重新缩放。数据重新缩放确保属性处于相同的比例。通常,属性会重新缩放到 0 和 1 的范围内。像梯度下降和 k 近邻这样的机器学习算法需要缩放后的数据。我们可以使用 scikit-learn Python 库的 MinMaxScaler 类重新缩放数据。
示例
在此示例中,我们将重新缩放之前使用过的皮马印第安人糖尿病数据集的数据。首先,将加载 CSV 数据(如前几章所述),然后借助 MinMaxScaler 类将其重新缩放到 0 和 1 的范围内。
以下脚本的前几行与我们在前几章加载 CSV 数据时编写的相同。
from pandas import read_csv from numpy import set_printoptions from sklearn import preprocessing path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(path, names=names) array = dataframe.values
现在,我们可以使用 MinMaxScaler 类将数据重新缩放到 0 和 1 的范围内。
data_scaler = preprocessing.MinMaxScaler(feature_range=(0,1)) data_rescaled = data_scaler.fit_transform(array)
我们还可以根据我们的选择汇总输出数据。这里,我们将精度设置为 1 并显示输出中的前 10 行。
set_printoptions(precision=1)
print ("\nScaled data:\n", data_rescaled[0:10])
输出
Scaled data: [[0.4 0.7 0.6 0.4 0. 0.5 0.2 0.5 1. ] [0.1 0.4 0.5 0.3 0. 0.4 0.1 0.2 0. ] [0.5 0.9 0.5 0. 0. 0.3 0.3 0.2 1. ] [0.1 0.4 0.5 0.2 0.1 0.4 0. 0. 0. ] [0. 0.7 0.3 0.4 0.2 0.6 0.9 0.2 1. ] [0.3 0.6 0.6 0. 0. 0.4 0.1 0.2 0. ] [0.2 0.4 0.4 0.3 0.1 0.5 0.1 0.1 1. ] [0.6 0.6 0. 0. 0. 0.5 0. 0.1 0. ] [0.1 1. 0.6 0.5 0.6 0.5 0. 0.5 1. ] [0.5 0.6 0.8 0. 0. 0. 0.1 0.6 1. ]]
从以上输出可以看出,所有数据都被重新缩放到 0 和 1 的范围内。
标准化
另一种有用的数据预处理技术是标准化。这用于重新缩放数据的每一行,使其长度为 1。它主要用于稀疏数据集中,在稀疏数据集中我们有很多零。我们可以使用 scikit-learn Python 库的 Normalizer 类重新缩放数据。
标准化的类型
在机器学习中,有两种标准化预处理技术,如下所示:
L1 标准化
它可以定义为一种标准化技术,它以这样一种方式修改数据集的值,即在每一行中,绝对值的总和始终为 1。它也称为最小绝对偏差。
示例
在此示例中,我们使用 L1 标准化技术来标准化之前使用过的皮马印第安人糖尿病数据集的数据。首先,将加载 CSV 数据,然后借助 Normalizer 类对其进行标准化。
以下脚本的前几行与我们在前几章加载 CSV 数据时编写的相同。
from pandas import read_csv from numpy import set_printoptions from sklearn.preprocessing import Normalizer path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv (path, names=names) array = dataframe.values
现在,我们可以使用带 L1 的 Normalizer 类来标准化数据。
Data_normalizer = Normalizer(norm='l1').fit(array) Data_normalized = Data_normalizer.transform(array)
我们还可以根据我们的选择汇总输出数据。这里,我们将精度设置为 2 并显示输出中的前 3 行。
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])
输出
Normalized data: [[0.02 0.43 0.21 0.1 0. 0.1 0. 0.14 0. ] [0. 0.36 0.28 0.12 0. 0.11 0. 0.13 0. ] [0.03 0.59 0.21 0. 0. 0.07 0. 0.1 0. ]]
L2 标准化
它可以定义为一种标准化技术,它以这样一种方式修改数据集的值,即在每一行中,平方和始终为 1。它也称为最小二乘法。
示例
在此示例中,我们使用 L2 标准化技术来标准化之前使用过的皮马印第安人糖尿病数据集的数据。首先,将加载 CSV 数据(如前几章所述),然后借助 Normalizer 类对其进行标准化。
以下脚本的前几行与我们在前几章加载 CSV 数据时编写的相同。
from pandas import read_csv from numpy import set_printoptions from sklearn.preprocessing import Normalizer path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv (path, names=names) array = dataframe.values
现在,我们可以使用带 L1 的 Normalizer 类来标准化数据。
Data_normalizer = Normalizer(norm='l2').fit(array) Data_normalized = Data_normalizer.transform(array)
我们还可以根据我们的选择汇总输出数据。这里,我们将精度设置为 2 并显示输出中的前 3 行。
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])
输出
Normalized data: [[0.03 0.83 0.4 0.2 0. 0.19 0. 0.28 0.01] [0.01 0.72 0.56 0.24 0. 0.22 0. 0.26 0. ] [0.04 0.92 0.32 0. 0. 0.12 0. 0.16 0.01]]
二值化
顾名思义,这是一种我们可以使数据二值化的技术。我们可以使用二值化阈值来使数据二值化。高于该阈值的值将转换为 1,低于该阈值的值将转换为 0。例如,如果我们选择阈值为 0.5,则高于它的数据集值将变为 1,低于它将变为 0。这就是为什么我们可以称之为二值化数据或阈值化数据。当我们的数据集中有概率并希望将其转换为清晰值时,此技术很有用。
我们可以使用 scikit-learn Python 库的 Binarizer 类对数据进行二值化。
示例
在此示例中,我们将重新缩放之前使用过的皮马印第安人糖尿病数据集的数据。首先,将加载 CSV 数据,然后借助 Binarizer 类将其转换为二值,即 0 和 1,具体取决于阈值。我们取 0.5 作为阈值。
以下脚本的前几行与我们在前几章加载 CSV 数据时编写的相同。
from pandas import read_csv from sklearn.preprocessing import Binarizer path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(path, names=names) array = dataframe.values
现在,我们可以使用 Binarize 类将数据转换为二值。
binarizer = Binarizer(threshold=0.5).fit(array) Data_binarized = binarizer.transform(array)
这里,我们显示输出中的前 5 行。
print ("\nBinary data:\n", Data_binarized [0:5])
输出
Binary data: [[1. 1. 1. 1. 0. 1. 1. 1. 1.] [1. 1. 1. 1. 0. 1. 0. 1. 0.] [1. 1. 1. 0. 0. 1. 1. 1. 1.] [1. 1. 1. 1. 1. 1. 0. 1. 0.] [0. 1. 1. 1. 1. 1. 1. 1. 1.]]
标准化
另一种有用的数据预处理技术,主要用于将数据属性转换为高斯分布。它将均值和标准差 (SD) 变换为标准高斯分布,均值为 0,标准差为 1。这种技术在像线性回归、逻辑回归这样的机器学习算法中很有用,这些算法假设输入数据集中存在高斯分布,并且在重新缩放的数据上产生更好的结果。我们可以借助 scikit-learn Python 库的 StandardScaler 类来标准化数据(均值 = 0,标准差 = 1)。
示例
在这个例子中,我们将重新缩放之前使用过的 Pima 印第安人糖尿病数据集的数据。首先,CSV 数据将被加载,然后借助 StandardScaler 类将其转换为均值为 0,标准差为 1 的高斯分布。
以下脚本的前几行与我们在前几章加载 CSV 数据时编写的相同。
from sklearn.preprocessing import StandardScaler from pandas import read_csv from numpy import set_printoptions path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(path, names=names) array = dataframe.values
现在,我们可以使用 StandardScaler 类来重新缩放数据。
data_scaler = StandardScaler().fit(array) data_rescaled = data_scaler.transform(array)
我们还可以根据自己的选择汇总输出数据。这里,我们将精度设置为 2,并在输出中显示前 5 行。
set_printoptions(precision=2)
print ("\nRescaled data:\n", data_rescaled [0:5])
输出
Rescaled data: [[ 0.64 0.85 0.15 0.91 -0.69 0.2 0.47 1.43 1.37] [-0.84 -1.12 -0.16 0.53 -0.69 -0.68 -0.37 -0.19 -0.73] [ 1.23 1.94 -0.26 -1.29 -0.69 -1.1 0.6 -0.11 1.37] [-0.84 -1. -0.16 0.15 0.12 -0.49 -0.92 -1.04 -0.73] [-1.14 0.5 -1.5 0.91 0.77 1.41 5.48 -0.02 1.37]]
数据标注
我们讨论了良好数据对于机器学习算法的重要性,以及在将数据发送到机器学习算法之前预处理数据的一些技术。这方面还有一个方面是数据标注。将具有适当标注的数据发送到机器学习算法也非常重要。例如,在分类问题的情况下,数据上存在许多标签形式的单词、数字等。
什么是标签编码?
大多数 sklearn 函数期望数据使用数字标签而不是单词标签。因此,我们需要将此类标签转换为数字标签。此过程称为标签编码。我们可以借助 scikit-learn Python 库的 LabelEncoder() 函数执行数据的标签编码。
示例
在以下示例中,Python 脚本将执行标签编码。
首先,导入所需的 Python 库,如下所示:
import numpy as np from sklearn import preprocessing
现在,我们需要提供输入标签,如下所示:
input_labels = ['red','black','red','green','black','yellow','white']
下一行代码将创建标签编码器并对其进行训练。
encoder = preprocessing.LabelEncoder() encoder.fit(input_labels)
接下来的脚本行将通过对随机排序列表进行编码来检查性能:
test_labels = ['green','red','black']
encoded_values = encoder.transform(test_labels)
print("\nLabels =", test_labels)
print("Encoded values =", list(encoded_values))
encoded_values = [3,0,4,1]
decoded_list = encoder.inverse_transform(encoded_values)
我们可以借助以下 Python 脚本获取编码值的列表:
print("\nEncoded values =", encoded_values)
print("\nDecoded labels =", list(decoded_list))
输出
Labels = ['green', 'red', 'black'] Encoded values = [1, 2, 0] Encoded values = [3, 0, 4, 1] Decoded labels = ['white', 'black', 'yellow', 'green']
Python 机器学习 - 数据特征选择
在上一章中,我们详细了解了如何预处理和准备机器学习数据。在本章中,让我们详细了解数据特征选择及其涉及的各个方面。
数据特征选择的重要性
机器学习模型的性能与其用于训练它的数据特征成正比。如果提供给模型的数据特征不相关,则机器学习模型的性能将受到负面影响。另一方面,使用相关的数据特征可以提高机器学习模型的准确性,特别是线性回归和逻辑回归。
现在问题出现了,什么是自动特征选择?它可以定义为一个过程,通过该过程,我们选择数据中与我们感兴趣的输出或预测变量最相关的特征。它也称为属性选择。
以下是在数据建模之前自动特征选择的一些好处:
在数据建模之前执行特征选择将减少过拟合。
在数据建模之前执行特征选择将提高机器学习模型的准确性。
在数据建模之前执行特征选择将减少训练时间。
特征选择技术
以下是我们可以用于在 Python 中对机器学习数据建模的自动特征选择技术:
单变量选择
这种特征选择技术在选择那些与预测变量具有最强关系的特征(借助统计检验)方面非常有用。我们可以借助 scikit-learn Python 库的 SelectKBest 类实现单变量特征选择技术。
示例
在这个例子中,我们将使用 Pima 印第安人糖尿病数据集,借助卡方统计检验选择 4 个具有最佳特征的属性。
from pandas import read_csv from numpy import set_printoptions from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(path, names=names) array = dataframe.values
接下来,我们将数组分离成输入和输出组件:
X = array[:,0:8] Y = array[:,8]
以下代码行将从数据集中选择最佳特征:
test = SelectKBest(score_func=chi2, k=4) fit = test.fit(X,Y)
我们还可以根据自己的选择汇总输出数据。这里,我们将精度设置为 2,并显示 4 个具有最佳特征的数据属性以及每个属性的最佳得分:
set_printoptions(precision=2)
print(fit.scores_)
featured_data = fit.transform(X)
print ("\nFeatured data:\n", featured_data[0:4])
输出
[ 111.52 1411.89 17.61 53.11 2175.57 127.67 5.39 181.3 ] Featured data: [[148. 0. 33.6 50. ] [ 85. 0. 26.6 31. ] [183. 0. 23.3 32. ] [ 89. 94. 28.1 21. ]]
递归特征消除
顾名思义,RFE(递归特征消除)特征选择技术递归地移除属性,并使用剩余属性构建模型。我们可以借助 scikit-learn Python 库的 RFE 类实现 RFE 特征选择技术。
示例
在这个例子中,我们将使用 RFE 和逻辑回归算法从 Pima 印第安人糖尿病数据集中选择具有最佳特征的 3 个最佳属性。
from pandas import read_csv from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(path, names=names) array = dataframe.values
接下来,我们将数组分离成其输入和输出组件:
X = array[:,0:8] Y = array[:,8]
以下代码行将从数据集中选择最佳特征:
model = LogisticRegression()
rfe = RFE(model, 3)
fit = rfe.fit(X, Y)
print("Number of Features: %d")
print("Selected Features: %s")
print("Feature Ranking: %s")
输出
Number of Features: 3 Selected Features: [ True False False False False True True False] Feature Ranking: [1 2 3 5 6 1 1 4]
我们可以在上面的输出中看到,RFE 选择 preg、mass 和 pedi 作为前 3 个最佳特征。它们在输出中标记为 1。
主成分分析 (PCA)
PCA,通常称为数据缩减技术,是一种非常有用的特征选择技术,因为它使用线性代数将数据集转换为压缩形式。我们可以借助 scikit-learn Python 库的 PCA 类实现 PCA 特征选择技术。我们可以选择输出中的主成分数量。
示例
在这个例子中,我们将使用 PCA 从 Pima 印第安人糖尿病数据集中选择 3 个最佳主成分。
from pandas import read_csv from sklearn.decomposition import PCA path = r'C:\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(path, names=names) array = dataframe.values
接下来,我们将数组分离成输入和输出组件:
X = array[:,0:8] Y = array[:,8]
以下代码行将从数据集中提取特征:
pca = PCA(n_components=3)
fit = pca.fit(X)
print("Explained Variance: %s") % fit.explained_variance_ratio_
print(fit.components_)
输出
Explained Variance: [ 0.88854663 0.06159078 0.02579012] [[ -2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-02 9.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03] [ 2.26488861e-02 9.72210040e-01 1.41909330e-01 -5.78614699e-02 -9.46266913e-02 4.69729766e-02 8.16804621e-04 1.40168181e-01] [ -2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-01 2.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]]
我们可以从上面的输出中观察到,3 个主成分与源数据几乎没有相似之处。
特征重要性
顾名思义,特征重要性技术用于选择重要特征。它基本上使用经过训练的监督分类器来选择特征。我们可以借助 scikit-learn Python 库的 ExtraTreeClassifier 类实现这种特征选择技术。
示例
在这个例子中,我们将使用 ExtraTreeClassifier 从 Pima 印第安人糖尿病数据集中选择特征。
from pandas import read_csv from sklearn.ensemble import ExtraTreesClassifier path = r'C:\Desktop\pima-indians-diabetes.csv' names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] dataframe = read_csv(data, names=names) array = dataframe.values
接下来,我们将数组分离成输入和输出组件:
X = array[:,0:8] Y = array[:,8]
以下代码行将从数据集中提取特征:
model = ExtraTreesClassifier() model.fit(X, Y) print(model.feature_importances_)
输出
[ 0.11070069 0.2213717 0.08824115 0.08068703 0.07281761 0.14548537 0.12654214 0.15415431]
从输出中,我们可以观察到每个属性都有分数。分数越高,该属性的重要性越高。
分类 - 简介
分类简介
分类可以定义为根据观察值或给定数据点预测类别或类别的过程。分类输出可以采用“黑色”或“白色”或“垃圾邮件”或“非垃圾邮件”等形式。
在数学上,分类是从输入变量 (X) 到输出变量 (Y) 的映射函数 (f) 的近似任务。它基本上属于监督机器学习,其中目标也与输入数据集一起提供。
分类问题的一个例子可能是电子邮件中的垃圾邮件检测。输出只有两个类别,“垃圾邮件”和“非垃圾邮件”;因此,这是一种二元分类。
要实现此分类,我们首先需要训练分类器。对于此示例,“垃圾邮件”和“非垃圾邮件”电子邮件将用作训练数据。成功训练分类器后,它可以用于检测未知电子邮件。
分类中的学习器类型
在分类问题方面,我们有两种类型的学习器:
懒惰学习器
顾名思义,这种学习器在存储训练数据后等待测试数据出现。只有在获得测试数据后才会进行分类。它们在训练上花费的时间较少,但在预测上花费的时间更多。懒惰学习器的例子包括 K 最近邻和基于案例的推理。
积极学习器
与懒惰学习器相反,积极学习器在存储训练数据后构建分类模型,而无需等待测试数据出现。它们在训练上花费的时间更多,但在预测上花费的时间更少。积极学习器的例子包括决策树、朴素贝叶斯和人工神经网络 (ANN)。
在 Python 中构建分类器
Scikit-learn 是一个用于机器学习的 Python 库,可用于在 Python 中构建分类器。在 Python 中构建分类器的步骤如下:
步骤 1:导入必要的 Python 包
要使用 scikit-learn 构建分类器,我们需要导入它。我们可以使用以下脚本导入它:
import sklearn
步骤 2:导入数据集
导入必要的包后,我们需要一个数据集来构建分类预测模型。我们可以从 sklearn 数据集中导入它,也可以根据需要使用其他数据集。我们将使用 sklearn 的乳腺癌威斯康星诊断数据库。我们可以借助以下脚本导入它:
from sklearn.datasets import load_breast_cancer
以下脚本将加载数据集;
data = load_breast_cancer()
我们还需要组织数据,这可以通过以下脚本完成:
label_names = data['target_names'] labels = data['target'] feature_names = data['feature_names'] features = data['data']
以下命令将打印标签的名称,在我们的数据库中为“恶性”和“良性”。
print(label_names)
上述命令的输出是标签的名称:
['malignant' 'benign']
这些标签映射到二进制值 0 和 1。恶性癌症由 0 表示,良性癌症由 1 表示。
这些标签的特征名称和特征值可以通过以下命令查看:
print(feature_names[0])
上述命令的输出是标签 0 即恶性癌症的特征名称:
mean radius
类似地,标签的特征名称可以如下生成:
print(feature_names[1])
上述命令的输出是标签 1 即良性癌症的特征名称:
mean texture
我们可以借助以下命令打印这些标签的特征:
print(features[0])
这将给出以下输出:
[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01 1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02 6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01 1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01 4.601e-01 1.189e-01]
我们可以借助以下命令打印这些标签的特征:
print(features[1])
这将给出以下输出:
[2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02 7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01 5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01 2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01 2.750e-01 8.902e-02]
步骤 3:将数据组织成训练集和测试集
由于我们需要在未见数据上测试我们的模型,因此我们将数据集分成两部分:训练集和测试集。我们可以使用 sklearn python 包的 train_test_split() 函数将数据分成数据集。以下命令将导入该函数:
from sklearn.model_selection import train_test_split
现在,下一个命令将数据分成训练数据和测试数据。在这个例子中,我们使用 40% 的数据进行测试,60% 的数据进行训练:
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)
步骤 4 - 模型评估
将数据分成训练集和测试集后,我们需要构建模型。我们将为此目的使用朴素贝叶斯算法。以下命令将导入 GaussianNB 模块 -
from sklearn.naive_bayes import GaussianNB
现在,如下所示初始化模型 -
gnb = GaussianNB()
接下来,借助以下命令,我们可以训练模型 -
model = gnb.fit(train, train_labels)
现在,为了评估目的,我们需要进行预测。可以使用 predict() 函数如下所示进行 -
preds = gnb.predict(test) print(preds)
这将给出以下输出:
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]
输出中上述一系列的 0 和 1 是恶性和良性肿瘤类别的预测值。
步骤 5 - 查找准确率
我们可以通过比较两个数组(即 test_labels 和 preds)来找到上一步构建的模型的准确率。我们将使用 accuracy_score() 函数来确定准确率。
from sklearn.metrics import accuracy_score print(accuracy_score(test_labels,preds)) 0.951754385965
以上输出显示朴素贝叶斯分类器的准确率为 95.17%。
分类评估指标
即使您已完成机器学习应用程序或模型的实现,工作也尚未完成。我们必须找出我们的模型有多有效?可能存在不同的评估指标,但我们必须谨慎选择,因为指标的选择会影响如何衡量和比较机器学习算法的性能。
以下是您可以根据您的数据集和问题类型从中选择的几个重要的分类评估指标 -
混淆矩阵
它是衡量分类问题性能的最简单方法,其中输出可以是两种或多种类型的类别。混淆矩阵不过是一个二维表,即“实际”和“预测”,此外,这两个维度都有“真阳性 (TP)”、“真阴性 (TN)”、“假阳性 (FP)”、“假阴性 (FN)”如下所示 -
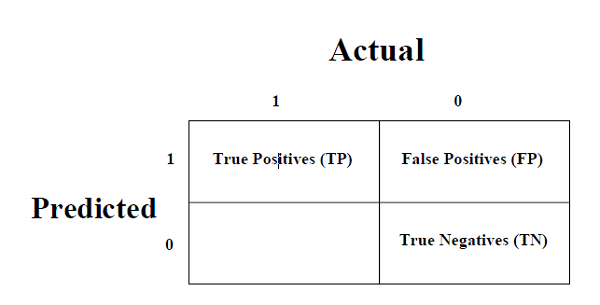
真阳性 (TP) - 当数据点的实际类别和预测类别均为 1 时。
真阴性 (TN) - 当数据点的实际类别和预测类别均为 0 时。
假阳性 (FP) - 当数据点的实际类别为 0 且预测类别为 1 时。
假阴性 (FN) - 当数据点的实际类别为 1 且预测类别为 0 时。
我们可以借助 sklearn 的 confusion_matrix() 函数找到混淆矩阵。借助以下脚本,我们可以找到上面构建的二元分类器的混淆矩阵 -
from sklearn.metrics import confusion_matrix
输出
[[ 73 7] [ 4 144]]
准确率
可以定义为我们的 ML 模型做出的正确预测的数量。我们可以很容易地通过混淆矩阵使用以下公式计算它 -
$$𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦=\frac{𝑇𝑃+𝑇𝑁}{𝑇𝑃+𝐹𝑃+𝐹𝑁+𝑇𝑁}$$对于上面构建的二元分类器,TP + TN = 73 + 144 = 217 且 TP + FP + FN + TN = 73 + 7 + 4 + 144 = 228。
因此,准确率 = 217/228 = 0.951754385965,与我们在创建二元分类器后计算的结果相同。
精确率
精确率,在文档检索中使用,可以定义为我们的 ML 模型返回的正确文档的数量。我们可以很容易地通过混淆矩阵使用以下公式计算它 -
$$𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛=\frac{𝑇𝑃}{𝑇𝑃+FP}$$对于上面构建的二元分类器,TP = 73 且 TP + FP = 73 + 7 = 80。
因此,精确率 = 73/80 = 0.915
召回率或灵敏度
召回率可以定义为我们的 ML 模型返回的阳性数量。我们可以很容易地通过混淆矩阵使用以下公式计算它 -
$$𝑅𝑒𝑐𝑎𝑙𝑙=\frac{𝑇𝑃}{𝑇𝑃+FN}$$对于上面构建的二元分类器,TP = 73 且 TP + FN = 73 + 4 = 77。
因此,精确率 = 73/77 = 0.94805
特异性
特异性,与召回率相反,可以定义为我们的 ML 模型返回的阴性数量。我们可以很容易地通过混淆矩阵使用以下公式计算它 -
$$𝑆𝑝𝑒𝑐𝑖𝑓𝑖𝑐𝑖𝑡𝑦=\frac{𝑇N}{𝑇N+FP}$$对于上面构建的二元分类器,TN = 144 且 TN + FP = 144 + 7 = 151。
因此,精确率 = 144/151 = 0.95364
各种 ML 分类算法
以下是几个重要的 ML 分类算法 -
逻辑回归
支持向量机 (SVM)
决策树
朴素贝叶斯
随机森林
我们将在后面的章节中详细讨论所有这些分类算法。
应用
分类算法的一些最重要的应用如下 -
语音识别
手写识别
生物识别
文档分类
分类算法 - 逻辑回归
逻辑回归简介
逻辑回归是一种监督学习分类算法,用于预测目标变量的概率。目标或因变量的性质是二分的,这意味着只有两种可能的类别。
简单来说,因变量本质上是二元的,数据编码为 1(代表成功/是)或 0(代表失败/否)。
在数学上,逻辑回归模型将 P(Y=1) 预测为 X 的函数。它是用于各种分类问题的最简单的 ML 算法之一,例如垃圾邮件检测、糖尿病预测、癌症检测等。
逻辑回归的类型
通常,逻辑回归指的是具有二元目标变量的二元逻辑回归,但它还可以预测目标变量的另外两个类别。根据这些类别的数量,逻辑回归可以分为以下类型 -
二元或二项式
在这种类型的分类中,因变量将只有两种可能的类型,要么是 1 要么是 0。例如,这些变量可能表示成功或失败、是或否、赢或输等。
多项式
在这种类型的分类中,因变量可以有 3 种或更多种可能的无序类型,或者没有定量意义的类型。例如,这些变量可能表示“A 型”或“B 型”或“C 型”。
有序
在这种类型的分类中,因变量可以有 3 种或更多种可能的顺序类型,或者具有定量意义的类型。例如,这些变量可能表示“差”或“好”、“非常好”、“优秀”,每个类别可以有 0、1、2、3 等分数。
逻辑回归假设
在深入研究逻辑回归的实现之前,我们必须了解以下关于它的假设 -
在二元逻辑回归的情况下,目标变量必须始终为二元,并且期望结果由因子水平 1 表示。
模型中不应存在多重共线性,这意味着自变量必须相互独立。
我们必须在模型中包含有意义的变量。
我们应该为逻辑回归选择一个大的样本量。
二元逻辑回归模型
逻辑回归最简单的形式是二元或二项式逻辑回归,其中目标或因变量只能有 2 种可能的类型,要么是 1 要么是 0。它允许我们对多个预测变量和二元/二项式目标变量之间的关系进行建模。在逻辑回归的情况下,线性函数基本上用作另一个函数(例如以下关系中的 𝑔)的输入 -
$h_{\theta}{(x)}=g(\theta^{T}x)𝑤ℎ𝑒𝑟𝑒 0≤h_{\theta}≤1$这里,𝑔 是逻辑或 sigmoid 函数,可以表示如下 -
$g(z)= \frac{1}{1+e^{-z}}𝑤ℎ𝑒𝑟𝑒 𝑧=\theta ^{T}𝑥$可以使用以下图形表示 sigmoid 曲线。我们可以看到 y 轴的值介于 0 和 1 之间,并在 0.5 处穿过轴。
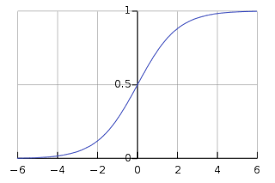
类别可以分为正类或负类。如果输出介于 0 和 1 之间,则它属于正类的概率。对于我们的实现,如果假设函数的输出 ≥0.5,则将其解释为正类,否则为负类。
我们还需要定义一个损失函数来衡量算法使用函数上的权重(用 theta 表示)的执行情况,如下所示 -
ℎ=𝑔(𝑋𝜃)
$J(\theta) = \frac{1}{m}.(-y^{T}log(h) - (1 -y)^Tlog(1-h))$现在,在定义损失函数后,我们的主要目标是最小化损失函数。这可以通过拟合权重来完成,这意味着通过增加或减少权重。借助损失函数对每个权重的导数,我们将能够知道哪些参数应该具有较高的权重,哪些参数应该具有较小的权重。
以下梯度下降方程告诉我们如果修改参数,损失将如何变化 -
$\frac{𝛿𝐽(𝜃)}{𝛿\theta_{j}}=\frac{1}{m}X^{T}(𝑔(𝑋𝜃)−𝑦)$Python 中的实现
现在,我们将用 Python 实现上述二元逻辑回归的概念。为此,我们使用了一个名为“iris”的多元花卉数据集,它有 3 个类别,每个类别有 50 个实例,但我们将使用前两个特征列。每个类别代表一种鸢尾花。
首先,我们需要导入必要的库,如下所示 -
import numpy as np import matplotlib.pyplot as plt import seaborn as sns from sklearn import datasets
接下来,加载 iris 数据集,如下所示 -
iris = datasets.load_iris() X = iris.data[:, :2] y = (iris.target != 0) * 1
我们可以绘制我们的训练数据,如下所示 -
plt.figure(figsize=(6, 6)) plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0') plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1') plt.legend();
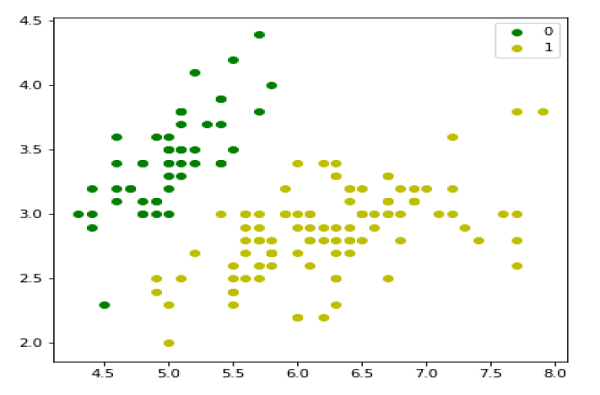
接下来,我们将定义 sigmoid 函数、损失函数和梯度下降,如下所示 -
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)
现在,初始化权重,如下所示 -
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
loss = self.__loss(h, y)
if(self.verbose ==True and i % 10000 == 0):
print(f'loss: {loss} \t')
借助以下脚本,我们可以预测输出概率 -
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
return self.predict_prob(X).round()
接下来,我们可以评估模型并绘制它,如下所示 -
model = LogisticRegression(lr=0.1, num_iter=300000) preds = model.predict(X) (preds == y).mean() plt.figure(figsize=(10, 6)) plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0') plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1') plt.legend() x1_min, x1_max = X[:,0].min(), X[:,0].max(), x2_min, x2_max = X[:,1].min(), X[:,1].max(), xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max)) grid = np.c_[xx1.ravel(), xx2.ravel()] probs = model.predict_prob(grid).reshape(xx1.shape) plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
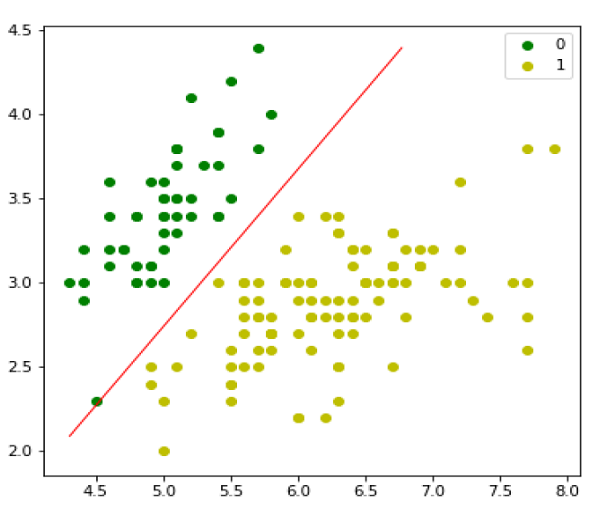
多项式逻辑回归模型
逻辑回归的另一种有用形式是多项式逻辑回归,其中目标或因变量可以有 3 种或更多种可能的无序类型,即没有定量意义的类型。
Python 中的实现
现在,我们将用 Python 实现上述多项式逻辑回归的概念。为此,我们使用 sklearn 中名为 digit 的数据集。
首先,我们需要导入必要的库,如下所示 -
Import sklearn from sklearn import datasets from sklearn import linear_model from sklearn import metrics from sklearn.model_selection import train_test_split
接下来,我们需要加载 digit 数据集 -
digits = datasets.load_digits()
现在,定义特征矩阵 (X) 和响应向量 (y),如下所示 -
X = digits.data y = digits.target
借助下一行代码,我们可以将 X 和 y 分割成训练集和测试集 -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
现在创建一个逻辑回归对象,如下所示 -
digreg = linear_model.LogisticRegression()
现在,我们需要使用训练集训练模型,如下所示 -
digreg.fit(X_train, y_train)
接下来,对测试集进行预测,如下所示 -
y_pred = digreg.predict(X_test)
接下来打印模型的准确率,如下所示 -
print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)
输出
Accuracy of Logistic Regression model is: 95.6884561891516
从以上输出中,我们可以看到模型的准确率约为 96%。
支持向量机 (SVM)
SVM 简介
支持向量机 (SVM) 是一种强大且灵活的监督机器学习算法,可用于分类和回归。但通常,它们用于分类问题。在 20 世纪 60 年代,SVM 首次被引入,但后来在 20 世纪 90 年代得到了改进。与其他机器学习算法相比,SVM 具有独特的实现方式。最近,由于它们能够处理多个连续和分类变量,因此它们非常受欢迎。
SVM 的工作原理
SVM 模型基本上是在多维空间中超平面中不同类别的表示。超平面将以迭代方式由 SVM 生成,以便可以最小化误差。SVM 的目标是将数据集划分为类别以找到最大间隔超平面 (MMH)。
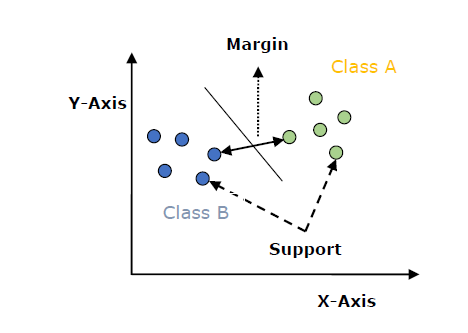
以下是 SVM 中的重要概念 -
支持向量 - 距离超平面最近的数据点称为支持向量。分离线将借助这些数据点来定义。
超平面 - 正如我们在上图中看到的,它是一个决策平面或空间,它将一组具有不同类别的对象分隔开来。
间隔 - 它可以定义为不同类别最近数据点之间两条线的间隙。它可以计算为从线到支持向量的垂直距离。大间隔被认为是好的间隔,小间隔被认为是坏的间隔。
SVM 的主要目标是将数据集划分为不同的类别,以找到最大间隔超平面 (MMH),这可以通过以下两个步骤完成:
首先,SVM 将迭代生成超平面,以最佳方式隔离类别。
然后,它将选择正确分离类别的超平面。
在 Python 中实现 SVM
为了在 Python 中实现 SVM,我们将从导入标准库开始,如下所示:
import numpy as np import matplotlib.pyplot as plt from scipy import stats import seaborn as sns; sns.set()
接下来,我们正在创建用于使用 SVM 进行分类的线性可分离数据样本数据集,来自 sklearn.dataset.sample_generator:
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=0.50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');
生成包含 100 个样本和 2 个簇的样本数据集后的输出如下:
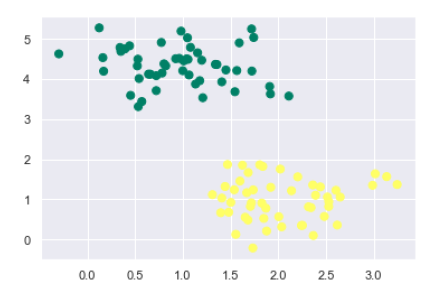
我们知道 SVM 支持判别式分类。它通过简单地在二维情况下找到一条线或在多维情况下找到一个流形来将类别彼此分开。它在上述数据集上实现如下:
xfit = np.linspace(-1, 3.5) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer') plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12) for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]: plt.plot(xfit, m * xfit + b, '-k') plt.xlim(-1, 3.5);
输出如下:
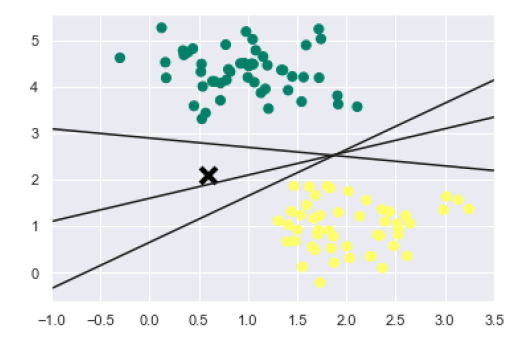
从上面的输出中我们可以看到,有三个不同的分离器可以完美地区分上述样本。
如前所述,SVM 的主要目标是将数据集划分为不同的类别,以找到最大间隔超平面 (MMH),因此,与其在类别之间绘制零线,不如在每条线周围绘制一定宽度的间隔,直到最近的点。它可以按如下方式完成:
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
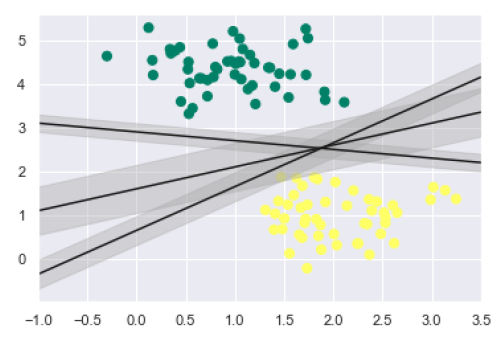
从输出中的上图中,我们可以很容易地观察到判别分类器内的“间隔”。SVM 将选择最大化间隔的线。
接下来,我们将使用 Scikit-Learn 的支持向量分类器来训练此数据的 SVM 模型。在这里,我们使用线性核来拟合 SVM,如下所示:
from sklearn.svm import SVC # "Support vector classifier" model = SVC(kernel='linear', C=1E10) model.fit(X, y)
输出如下:
SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape='ovr', degree=3, gamma='auto_deprecated', kernel='linear', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False)
现在,为了更好地理解,以下将绘制二维 SVC 的决策函数:
def decision_function(model, ax=None, plot_support=True):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
为了评估模型,我们需要创建网格,如下所示:
x = np.linspace(xlim[0], xlim[1], 30) y = np.linspace(ylim[0], ylim[1], 30) Y, X = np.meshgrid(y, x) xy = np.vstack([X.ravel(), Y.ravel()]).T P = model.decision_function(xy).reshape(X.shape)
接下来,我们需要绘制决策边界和间隔,如下所示:
ax.contour(X, Y, P, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
现在,类似地绘制支持向量,如下所示:
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)
现在,使用此函数拟合我们的模型,如下所示:
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer') decision_function(model);
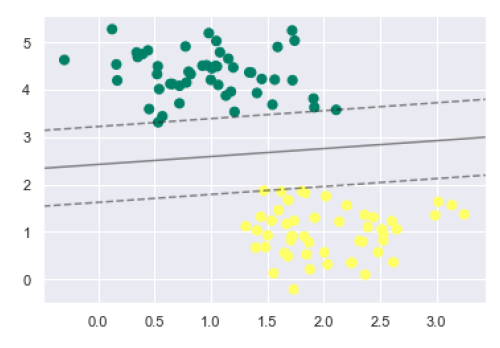
从上面的输出中我们可以观察到,一个 SVM 分类器适合具有间隔(即虚线)和支持向量的数据,这些支持向量是此拟合的关键元素,并接触到虚线。这些支持向量点存储在分类器的 support_vectors_ 属性中,如下所示:
model.support_vectors_
输出如下:
array([[0.5323772 , 3.31338909], [2.11114739, 3.57660449], [1.46870582, 1.86947425]])
SVM 核函数
在实践中,SVM 算法是使用核函数来实现的,该核函数将输入数据空间转换为所需的形式。SVM 使用一种称为核技巧的技术,其中核函数将低维输入空间转换为高维空间。简单来说,核函数通过增加维度将不可分离问题转换为可分离问题。它使 SVM 更加强大、灵活和准确。以下是 SVM 使用的一些核函数类型:
线性核函数
它可以用作任何两个观测值之间的点积。线性核函数的公式如下:
k(x,xi) = sum(x*xi)
从上面的公式中,我们可以看到两个向量(例如 𝑥 和 𝑥𝑖)之间的乘积是每对输入值的乘积之和。
多项式核函数
它是线性核函数的更通用形式,可以区分曲线或非线性输入空间。以下是多项式核函数的公式:
K(x, xi) = 1 + sum(x * xi)^d
这里 d 是多项式的次数,我们需要在学习算法中手动指定它。
径向基函数 (RBF) 核函数
RBF 核函数主要用于 SVM 分类,它将输入空间映射到无限维空间。以下公式用数学方法解释了它:
K(x,xi) = exp(-gamma * sum((x – xi^2))
这里,gamma 的范围为 0 到 1。我们需要在学习算法中手动指定它。gamma 的一个好的默认值为 0.1。
由于我们已经实现了线性可分离数据的 SVM,因此我们可以使用核函数在 Python 中实现不可分离的数据。它可以通过使用核函数来完成。
示例
以下是如何使用核函数创建 SVM 分类器的示例。我们将使用 scikit-learn 中的 iris 数据集:
我们将从导入以下包开始:
import pandas as pd import numpy as np from sklearn import svm, datasets import matplotlib.pyplot as plt
现在,我们需要加载输入数据:
iris = datasets.load_iris()
从这个数据集中,我们取前两个特征,如下所示:
X = iris.data[:, :2] y = iris.target
接下来,我们将使用原始数据绘制 SVM 边界,如下所示:
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 h = (x_max / x_min)/100 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) X_plot = np.c_[xx.ravel(), yy.ravel()]
现在,我们需要提供正则化参数的值,如下所示:
C = 1.0
接下来,可以创建 SVM 分类器对象,如下所示:
Svc_classifier = svm.SVC(kernel='linear', C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')
输出
Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')
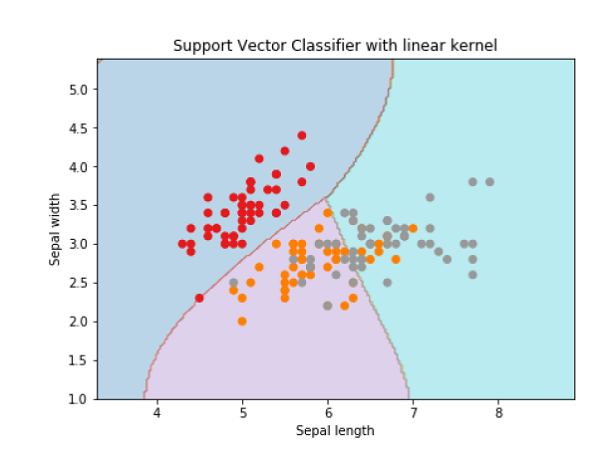
为了使用rbf核函数创建 SVM 分类器,我们可以将核函数更改为rbf,如下所示:
Svc_classifier = svm.SVC(kernel='rbf', gamma =‘auto’,C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')
输出
Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')
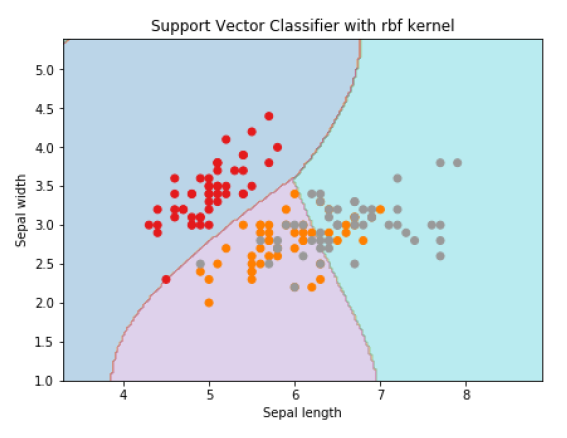
我们将 gamma 的值设置为“auto”,但您也可以提供其值(介于 0 到 1 之间)。
SVM 分类器的优缺点
SVM 分类器的优点
SVM 分类器提供很高的准确性,并且适用于高维空间。SVM 分类器基本上使用训练点的子集,因此最终使用非常少的内存。
SVM 分类器的缺点
它们的训练时间较长,因此在实践中不适用于大型数据集。另一个缺点是 SVM 分类器不适用于重叠类别。
分类算法 - 决策树
决策树简介
通常,决策树分析是一种预测建模工具,可以应用于许多领域。决策树可以通过算法方法构建,该方法可以根据不同的条件以不同的方式拆分数据集。决策树是最强大的算法,属于监督算法类别。
它们可用于分类和回归任务。树的两个主要实体是决策节点(数据在其中被拆分)和叶子节点(我们在其中获得结果)。下面给出了一个用于预测一个人是否健康(提供各种信息,如年龄、饮食习惯和锻炼习惯)的二叉树示例:
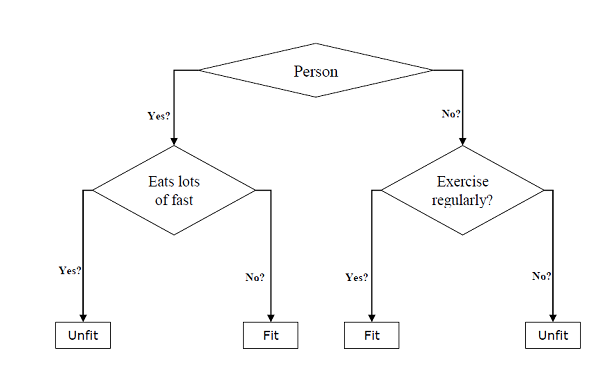
在上图的决策树中,问题是决策节点,最终结果是叶子节点。我们有以下两种类型的决策树:
分类决策树 - 在这种决策树中,决策变量是分类变量。上面的决策树是分类决策树的一个例子。
回归决策树 - 在这种决策树中,决策变量是连续变量。
实现决策树算法
基尼指数
它是用于评估数据集中二元拆分的成本函数的名称,并且适用于分类目标变量“成功”或“失败”。
基尼指数的值越高,同质性越高。完美的基尼指数值为 0,最差为 0.5(对于 2 类问题)。可以使用以下步骤计算拆分的基尼指数:
首先,使用公式 p^2+q^2 计算子节点的基尼指数,它是成功和失败概率的平方和。
接下来,使用该拆分每个节点的加权基尼分数计算拆分的基尼指数。
分类和回归树 (CART) 算法使用基尼方法生成二元拆分。
拆分创建
拆分基本上包括数据集中的一个属性和一个值。我们可以借助以下三个部分在数据集中创建拆分:
部分 1 - 计算基尼分数:我们刚刚在上一节中讨论了这部分内容。
部分 2 - 拆分数据集:它可以定义为将数据集分成两个行列表,其中包含属性的索引和该属性的拆分值。从数据集中获得两个组(右组和左组)后,我们可以使用在第一部分中计算出的基尼分数来计算拆分值。拆分值将决定属性将驻留在哪个组中。
部分 3 - 评估所有拆分:找到基尼分数和拆分数据集后的下一部分是对所有拆分进行评估。为此,我们首先必须检查与每个属性相关联的每个值作为候选拆分。然后,我们需要通过评估拆分的成本找到最佳的拆分。最佳拆分将用作决策树中的节点。
构建树
众所周知,树具有根节点和终端节点。创建根节点后,我们可以通过以下两个部分构建树:
部分 1:终端节点创建
在创建决策树的终端节点时,一个重要的点是决定何时停止树的增长或创建进一步的终端节点。这可以通过使用以下两个标准来完成:最大树深度和最小节点记录:
最大树深度 - 顾名思义,这是根节点之后树中节点的最大数量。一旦树达到最大深度(即一旦树获得最大数量的终端节点),我们必须停止添加终端节点。
最小节点记录 - 它可以定义为给定节点负责的训练模式的最小数量。一旦树达到这些最小节点记录或低于此最小值,我们必须停止添加终端节点。
终端节点用于进行最终预测。
部分 2:递归拆分
在我们了解了何时创建终端节点后,现在我们可以开始构建我们的树了。递归拆分是一种构建树的方法。在这种方法中,一旦创建了一个节点,我们就可以在通过拆分数据集生成的每个数据组上递归地创建子节点(添加到现有节点的节点),方法是反复调用相同的函数。
预测
构建决策树后,我们需要对其进行预测。基本上,预测涉及使用特定提供的行数据遍历决策树。
我们可以借助递归函数进行预测,就像上面所做的那样。相同的预测例程将与左子节点或右子节点一起再次调用。
假设
在创建决策树时,我们做出以下一些假设:
在准备决策树时,训练集作为根节点。
决策树分类器更喜欢特征值是分类的。如果您想使用连续值,则必须在构建模型之前对其进行离散化。
根据属性的值,记录被递归地分布。
统计方法将用于将属性放置在任何节点位置(即作为根节点或内部节点)。
Python 中的实现
示例
在以下示例中,我们将对 Pima 印第安人糖尿病数据集实现决策树分类器:
首先,从导入必要的 Python 包开始:
import pandas as pd from sklearn.tree import DecisionTreeClassifier from sklearn.model_selection import train_test_split
接下来,从其网络链接下载 iris 数据集,如下所示:
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label'] pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names) pima.head()
pregnant glucose bp skin insulin bmi pedigree age label 0 6 148 72 35 0 33.6 0.627 50 1 1 1 85 66 29 0 26.6 0.351 31 0 2 8 183 64 0 0 23.3 0.672 32 1 3 1 89 66 23 94 28.1 0.167 21 0 4 0 137 40 35 168 43.1 2.288 33 1
现在,将数据集拆分为特征和目标变量,如下所示:
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree'] X = pima[feature_cols] # Features y = pima.label # Target variable
接下来,我们将数据划分为训练集和测试集。以下代码将数据集拆分为 70% 的训练数据和 30% 的测试数据:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
接下来,使用 sklearn 的 DecisionTreeClassifier 类训练模型,如下所示:
clf = DecisionTreeClassifier() clf = clf.fit(X_train,y_train)
最后,我们需要进行预测。这可以通过以下脚本完成:
y_pred = clf.predict(X_test)
接下来,我们可以获取准确率得分、混淆矩阵和分类报告,如下所示:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)
输出
Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
precision recall f1-score support
0 0.72 0.79 0.75 146
1 0.57 0.46 0.51 85
micro avg 0.67 0.67 0.67 231
macro avg 0.64 0.63 0.63 231
weighted avg 0.66 0.67 0.66 231
Accuracy: 0.670995670995671
决策树可视化
可以使用以下代码可视化上述决策树:
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())
分类算法 - 朴素贝叶斯
朴素贝叶斯算法简介
朴素贝叶斯算法是一种分类技术,它基于贝叶斯定理,并假设所有预测变量之间相互独立。简单来说,这个假设就是指在一个类中某个特征的存在与同一类中其他特征的存在是相互独立的。例如,一部手机如果具有触摸屏、互联网功能、良好的摄像头等,就可以被认为是智能手机。尽管所有这些特征都是相互依赖的,但它们都独立地对手机是否是智能手机的概率做出贡献。
在贝叶斯分类中,主要关注的是寻找后验概率,即给定一些观察到的特征后标签的概率,𝑃(𝐿 | 𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠)。借助贝叶斯定理,我们可以用以下定量形式表示:
$P(L |features)= \frac{P(L)P(features |L)}{𝑃(𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠)}$其中,𝑃(𝐿 | 𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠) 是类的后验概率。
𝑃(𝐿) 是类的先验概率。
𝑃(𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠 | 𝐿) 是似然度,即给定类别的预测变量的概率。
𝑃(𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠) 是预测变量的先验概率。
使用 Python 中的朴素贝叶斯构建模型
Python 库 Scikit-learn 是一个非常有用的库,可以帮助我们在 Python 中构建朴素贝叶斯模型。在 Scikit-learn Python 库下,我们有以下三种类型的朴素贝叶斯模型:
高斯朴素贝叶斯
这是最简单的朴素贝叶斯分类器,它假设每个标签的数据都来自一个简单的高斯分布。
多项式朴素贝叶斯
另一种有用的朴素贝叶斯分类器是多项式朴素贝叶斯,其中假设特征是从一个简单的多项式分布中提取的。这种类型的朴素贝叶斯最适合表示离散计数的特征。
伯努利朴素贝叶斯
另一个重要的模型是伯努利朴素贝叶斯,其中假设特征是二元的(0 和 1)。使用“词袋”模型的文本分类可以作为伯努利朴素贝叶斯的应用。
示例
根据我们的数据集,我们可以选择上面解释的任何一个朴素贝叶斯模型。在这里,我们将在 Python 中实现高斯朴素贝叶斯模型:
我们将从所需的导入开始,如下所示:
import numpy as np import matplotlib.pyplot as plt import seaborn as sns; sns.set()
现在,通过使用 Scikit-learn 的 make_blobs() 函数,我们可以生成具有高斯分布的点集,如下所示:
from sklearn.datasets import make_blobs X, y = make_blobs(300, 2, centers=2, random_state=2, cluster_std=1.5) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');
接下来,为了使用 GaussianNB 模型,我们需要导入并创建其对象,如下所示:
from sklearn.naive_bayes import GaussianNB model_GBN = GaussianNB() model_GNB.fit(X, y);
现在,我们必须进行预测。这可以在生成一些新数据后完成,如下所示:
rng = np.random.RandomState(0) Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2) ynew = model_GNB.predict(Xnew)
接下来,我们正在绘制新数据以找到其边界:
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer') lim = plt.axis() plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='summer', alpha=0.1) plt.axis(lim);
现在,借助以下几行代码,我们可以找到第一个和第二个标签的后验概率:
yprob = model_GNB.predict_proba(Xnew) yprob[-10:].round(3)
输出
array([[0.998, 0.002],
[1. , 0. ],
[0.987, 0.013],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[0. , 1. ],
[0.986, 0.014]])
优缺点
优点
以下是使用朴素贝叶斯分类器的一些优点:
朴素贝叶斯分类易于实现且速度快。
它比逻辑回归等判别模型收敛得更快。
它需要较少的训练数据。
它本质上具有高度可扩展性,或者它们与预测变量和数据点的数量线性扩展。
它可以进行概率预测,并且可以处理连续数据和离散数据。
朴素贝叶斯分类算法既可以用于二元分类问题,也可以用于多类分类问题。
缺点
以下是使用朴素贝叶斯分类器的一些缺点:
朴素贝叶斯分类的一个最重要的缺点是其强特征独立性,因为在现实生活中,几乎不可能有一组完全相互独立的特征。
朴素贝叶斯分类的另一个问题是其“零频率”,这意味着如果一个分类变量有一个类别但在训练数据集中没有观察到,那么朴素贝叶斯模型将为其分配零概率,并且将无法进行预测。
朴素贝叶斯分类的应用
以下是朴素贝叶斯分类的一些常见应用:
实时预测 - 由于其易于实现和快速计算,它可以用于进行实时预测。
多类预测 - 朴素贝叶斯分类算法可以用于预测目标变量多个类的后验概率。
文本分类 - 由于具有多类预测的功能,朴素贝叶斯分类算法非常适合文本分类。因此,它也用于解决垃圾邮件过滤和情感分析等问题。
推荐系统 - 除了协同过滤等算法外,朴素贝叶斯还可以构建推荐系统,用于过滤未见信息并预测用户是否喜欢给定资源。
分类算法 - 随机森林
介绍
随机森林是一种监督学习算法,可用于分类和回归。但是,它主要用于分类问题。众所周知,森林是由树木组成的,树木越多,森林就越茂盛。类似地,随机森林算法会在数据样本上创建决策树,然后从每个决策树中获取预测结果,最后通过投票选择最佳解决方案。它是一种集成方法,优于单个决策树,因为它通过平均结果来减少过拟合。
随机森林算法的工作原理
我们可以通过以下步骤了解随机森林算法的工作原理:
步骤1 - 首先,从给定的数据集中选择随机样本。
步骤2 - 接下来,该算法将为每个样本构建一棵决策树。然后,它将从每个决策树中获取预测结果。
步骤3 - 在此步骤中,将对每个预测结果进行投票。
步骤4 - 最后,选择投票最多的预测结果作为最终预测结果。
下图将说明其工作原理:
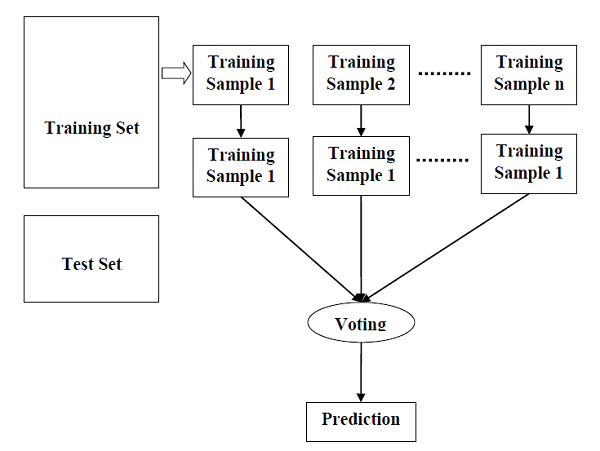
Python 中的实现
首先,从导入必要的 Python 包开始:
import numpy as np import matplotlib.pyplot as plt import pandas as pd
接下来,从其网络链接下载 iris 数据集,如下所示:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
接下来,我们需要为数据集分配列名,如下所示:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
现在,我们需要将数据集读取到 pandas 数据框中,如下所示:
dataset = pd.read_csv(path, names=headernames) dataset.head()
萼片长度 |
萼片宽度 |
花瓣长度 |
花瓣宽度 |
类别 |
|
|---|---|---|---|---|---|
0 |
5.1 |
3.5 |
1.4 |
0.2 |
Iris-setosa |
1 |
4.9 |
3.0 |
1.4 |
0.2 |
Iris-setosa |
2 |
4.7 |
3.2 |
1.3 |
0.2 |
Iris-setosa |
3 |
4.6 |
3.1 |
1.5 |
0.2 |
Iris-setosa |
4 |
5.0 |
3.6 |
1.4 |
0.2 |
Iris-setosa |
数据预处理将借助以下脚本行完成:
X = dataset.iloc[:, :-1].values y = dataset.iloc[:, 4].values
接下来,我们将数据划分为训练集和测试集。以下代码将数据集拆分为 70% 的训练数据和 30% 的测试数据:
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)
接下来,使用 sklearn 的 RandomForestClassifier 类训练模型,如下所示:
from sklearn.ensemble import RandomForestClassifier classifier = RandomForestClassifier(n_estimators=50) classifier.fit(X_train, y_train)
最后,我们需要进行预测。这可以通过以下脚本完成:
y_pred = classifier.predict(X_test)
接下来,打印结果,如下所示:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)
输出
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777
随机森林的优缺点
优点
以下是随机森林算法的优点:
它通过平均或组合不同决策树的结果来克服过拟合问题。
与单个决策树相比,随机森林适用于更广泛的数据项。
随机森林的方差小于单个决策树。
随机森林非常灵活,并且具有很高的准确性。
随机森林算法不需要对数据进行缩放。即使在提供未缩放的数据后,它也能保持良好的准确性。
随机森林算法不需要对数据进行缩放。即使在提供未缩放的数据后,它也能保持良好的准确性。
缺点
以下是随机森林算法的缺点:
复杂性是随机森林算法的主要缺点。
构建随机森林比决策树更困难且耗时。
实现随机森林算法需要更多计算资源。
当我们有一大堆决策树时,它不太直观。
与其他算法相比,使用随机森林进行预测非常耗时。
回归算法 - 概述
回归简介
回归是另一个重要且广泛使用的统计和机器学习工具。基于回归的任务的主要目标是预测输出标签或响应,这些标签或响应是给定输入数据的连续数值。输出将基于模型在训练阶段学到的内容。基本上,回归模型使用输入数据特征(自变量)及其相应的连续数值输出值(因变量或结果变量)来学习输入和相应输出之间的特定关联。
回归模型的类型
回归模型有以下两种类型:
简单回归模型 - 这是最基本的回归模型,其中预测是根据数据的单个单变量特征形成的。
多元回归模型 - 顾名思义,在这种回归模型中,预测是根据数据的多个特征形成的。
在 Python 中构建回归器
Python 中的回归器模型的构建方式与我们构建分类器的方式类似。Scikit-learn,一个用于机器学习的 Python 库,也可以用于在 Python 中构建回归器。
在以下示例中,我们将构建一个基本回归模型,该模型将一条线拟合到数据上,即线性回归器。在 Python 中构建回归器的必要步骤如下:
步骤 1:导入必要的 Python 包
为了使用 scikit-learn 构建回归器,我们需要将其与其他必要的包一起导入。我们可以使用以下脚本导入它:
import numpy as np from sklearn import linear_model import sklearn.metrics as sm import matplotlib.pyplot as plt
步骤 2:导入数据集
导入必要的包后,我们需要一个数据集来构建回归预测模型。我们可以从 sklearn 数据集中导入它,也可以根据我们的需要使用其他数据集。我们将使用我们保存的输入数据。我们可以借助以下脚本导入它:
input = r'C:\linear.txt'
接下来,我们需要加载此数据。我们使用 np.loadtxt 函数来加载它。
input_data = np.loadtxt(input, delimiter=',') X, y = input_data[:, :-1], input_data[:, -1]
步骤 3:将数据组织成训练集和测试集
由于我们需要在未见过的数据上测试我们的模型,因此我们将数据集分成两部分:训练集和测试集。以下命令将执行此操作:
training_samples = int(0.6 * len(X)) testing_samples = len(X) - num_training X_train, y_train = X[:training_samples], y[:training_samples] X_test, y_test = X[training_samples:], y[training_samples:]
步骤4- 模型评估和预测
将数据划分为训练集和测试集后,我们需要构建模型。我们将为此目的使用 Scikit-learn 的 LineaRegression() 函数。以下命令将创建一个线性回归器对象。
reg_linear= linear_model.LinearRegression()
接下来,使用训练样本训练此模型,如下所示:
reg_linear.fit(X_train, y_train)
现在,最后我们需要使用测试数据进行预测。
y_test_pred = reg_linear.predict(X_test)
步骤5- 绘制和可视化
预测后,我们可以使用以下脚本绘制和可视化它:
plt.scatter(X_test, y_test, color='red') plt.plot(X_test, y_test_pred, color='black', linewidth=2) plt.xticks(()) plt.yticks(()) plt.show()
输出
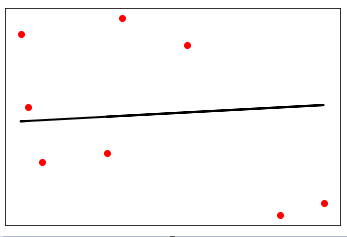
在上面的输出中,我们可以看到数据点之间的回归线。
步骤6- 性能计算 - 我们还可以使用各种性能指标来计算回归模型的性能,如下所示:
print("Regressor model performance:")
print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))
输出
Regressor model performance: Mean absolute error(MAE) = 1.78 Mean squared error(MSE) = 3.89 Median absolute error = 2.01 Explain variance score = -0.09 R2 score = -0.09
机器学习回归算法的类型
最有用的和流行的机器学习回归算法是线性回归算法,它进一步分为两种类型:
简单线性回归算法
多元线性回归算法。
我们将在下一章讨论它并在 Python 中实现它。
应用
机器学习回归算法的应用如下:
预测或预测分析 - 回归的一个重要用途是预测或预测分析。例如,我们可以预测 GDP、油价或简单来说是随时间变化的定量数据。
优化 - 我们可以借助回归来优化业务流程。例如,商店经理可以创建一个统计模型来了解客户到来的高峰时间。
错误校正 - 在业务中,做出正确的决策与优化业务流程同等重要。回归也可以帮助我们做出正确的决策,以及纠正已实施的决策。
经济学 - 它是经济学中最常用的工具。我们可以使用回归来预测供应、需求、消费、库存投资等。
金融 − 金融公司始终希望最小化投资组合风险,并想知道影响客户的因素。所有这些都可以借助回归模型进行预测。
回归算法 - 线性回归
线性回归简介
线性回归可以定义为一种统计模型,它分析因变量与给定的一组自变量之间的线性关系。变量之间的线性关系意味着,当一个或多个自变量的值发生变化(增加或减少)时,因变量的值也会相应地发生变化(增加或减少)。
从数学上讲,这种关系可以用以下方程表示:
Y = mX + b
这里,Y 是我们试图预测的因变量
X 是我们用来进行预测的自变量。
m 是回归线的斜率,表示 X 对 Y 的影响
b 是一个常数,称为 Y 截距。如果 X = 0,则 Y 等于 b。
此外,线性关系可以是正向的或负向的,如下所述:
正线性关系
如果自变量和因变量都增加,则线性关系称为正线性关系。这可以通过以下图形理解:
负线性关系
如果自变量增加而因变量减少,则线性关系称为负线性关系。这可以通过以下图形理解:
线性回归的类型
线性回归主要分为以下两种类型:
简单线性回归
多元线性回归
简单线性回归 (SLR)
它是线性回归最基本的版本,使用单个特征预测响应。SLR 的假设是这两个变量之间存在线性关系。
Python 实现
我们可以通过两种方式在 Python 中实现 SLR,一种是提供您自己的数据集,另一种是使用 scikit-learn Python 库中的数据集。
示例 1 − 在以下 Python 实现示例中,我们使用自己的数据集。
首先,我们将从导入必要的包开始,如下所示:
%matplotlib inline import numpy as np import matplotlib.pyplot as plt
接下来,定义一个函数,该函数将计算 SLR 的重要值:
def coef_estimation(x, y):
以下脚本行将给出观测值的数量 n:
n = np.size(x)
x 和 y 向量的平均值可以计算如下:
m_x, m_y = np.mean(x), np.mean(y)
我们可以找到交叉偏差和关于 x 的偏差,如下所示:
SS_xy = np.sum(y*x) - n*m_y*m_x SS_xx = np.sum(x*x) - n*m_x*m_x
接下来,回归系数,即 b 可以计算如下:
b_1 = SS_xy / SS_xx b_0 = m_y - b_1*m_x return(b_0, b_1)
接下来,我们需要定义一个函数,该函数将绘制回归线并预测响应向量:
def plot_regression_line(x, y, b):
以下脚本行将实际点绘制为散点图:
plt.scatter(x, y, color = "m", marker = "o", s = 30)
以下脚本行将预测响应向量:
y_pred = b[0] + b[1]*x
以下脚本行将绘制回归线并在其上添加标签:
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()
最后,我们需要定义 main() 函数来提供数据集并调用我们上面定义的函数:
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()
输出
Estimated coefficients: b_0 = 154.5454545454545 b_1 = 117.87878787878788
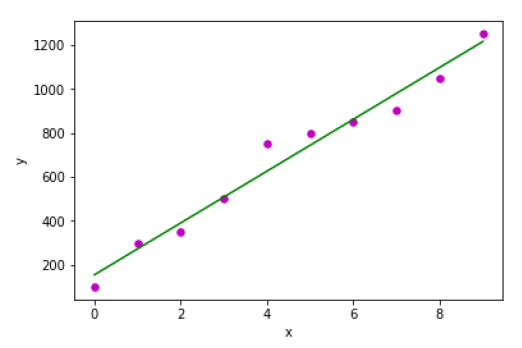
示例 2 − 在以下 Python 实现示例中,我们使用 scikit-learn 中的糖尿病数据集。
首先,我们将从导入必要的包开始,如下所示:
%matplotlib inline import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model from sklearn.metrics import mean_squared_error, r2_score
接下来,我们将加载糖尿病数据集并创建其对象:
diabetes = datasets.load_diabetes()
由于我们正在实现 SLR,因此我们将只使用一个特征,如下所示:
X = diabetes.data[:, np.newaxis, 2]
接下来,我们需要将数据拆分为训练集和测试集,如下所示:
X_train = X[:-30] X_test = X[-30:]
接下来,我们需要将目标拆分为训练集和测试集,如下所示:
y_train = diabetes.target[:-30] y_test = diabetes.target[-30:]
现在,要训练模型,我们需要创建线性回归对象,如下所示:
regr = linear_model.LinearRegression()
接下来,使用训练集训练模型,如下所示:
regr.fit(X_train, y_train)
接下来,使用测试集进行预测,如下所示:
y_pred = regr.predict(X_test)
接下来,我们将打印一些系数,例如 MSE、方差分数等,如下所示:
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))
现在,绘制输出,如下所示:
plt.scatter(X_test, y_test, color='blue') plt.plot(X_test, y_pred, color='red', linewidth=3) plt.xticks(()) plt.yticks(()) plt.show()
输出
Coefficients: [941.43097333] Mean squared error: 3035.06 Variance score: 0.41
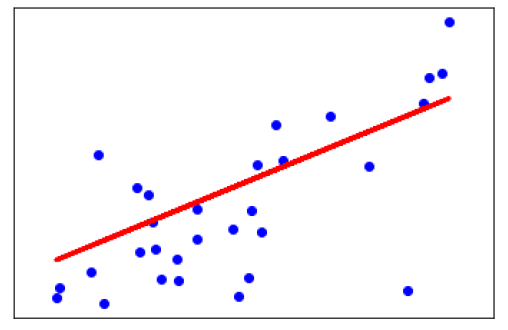
多元线性回归 (MLR)
它是简单线性回归的扩展,使用两个或多个特征预测响应。从数学上讲,我们可以解释如下:
考虑一个具有 n 个观测值、p 个特征(即自变量)和 y 作为单个响应(即因变量)的数据集,则 p 个特征的回归线可以计算如下:
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}$这里,h(xi) 是预测的响应值,b0、b1、b2…、bp 是回归系数。
多元线性回归模型始终包括数据中的误差,称为残差误差,这会改变计算方式,如下所示:
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}+e_{i}$我们也可以将上述方程写成如下形式:
$y_{i}=h(x_{i})+e_{i}$ 或 $e_{i}= y_{i} - h(x_{i})$Python 实现
在这个例子中,我们将使用 scikit learn 中的波士顿房价数据集:
首先,我们将从导入必要的包开始,如下所示:
%matplotlib inline import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model, metrics
接下来,加载数据集,如下所示:
boston = datasets.load_boston(return_X_y=False)
以下脚本行将定义特征矩阵 X 和响应向量 Y:
X = boston.data y = boston.target
接下来,将数据集拆分为训练集和测试集,如下所示:
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)
现在,创建线性回归对象并训练模型,如下所示:
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()
输出
Coefficients: [-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00 -1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00 3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03 -7.92395217e-01] Variance score: 0.709454060230326
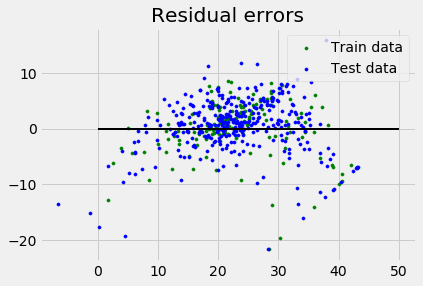
假设
以下是线性回归模型对数据集做出的一些假设:
多重共线性 − 线性回归模型假设数据中几乎没有或没有多重共线性。基本上,当自变量或特征之间存在依赖关系时,就会发生多重共线性。
自相关 − 线性回归模型假设的另一个假设是数据中几乎没有或没有自相关。基本上,当残差误差之间存在依赖关系时,就会发生自相关。
变量之间的关系 − 线性回归模型假设响应变量和特征变量之间的关系必须是线性的。
聚类算法 - 概述
聚类简介
聚类方法是最有用的无监督机器学习方法之一。这些方法用于查找数据样本之间的相似性和关系模式,然后根据特征将这些样本聚类到具有相似性的组中。
聚类很重要,因为它确定了当前未标记数据中固有的分组。它们基本上对数据点做出一些假设来构成它们的相似性。每个假设将构建不同的但同样有效的聚类。
例如,下图显示了聚类系统将相似类型的数据组合到不同聚类中的情况:
聚类形成方法
聚类不一定以球形形式形成。以下是其他一些聚类形成方法:
基于密度的
在这些方法中,聚类形成密集区域。这些方法的优点是它们具有良好的准确性和合并两个聚类的能力。例如,基于密度的噪声应用空间聚类 (DBSCAN)、用于识别聚类结构的排序点 (OPTICS) 等。
基于层次的
在这些方法中,聚类形成树状结构,基于层次结构。它们有两个类别,即凝聚的(自下而上的方法)和分裂的(自上而下的方法)。例如,使用代表的聚类 (CURE)、基于层次结构的平衡迭代减少聚类 (BIRCH) 等。
划分
在这些方法中,通过将对象划分为 k 个聚类来形成聚类。聚类的数量将等于分区的数量。例如,K 均值、基于随机搜索的大型应用程序聚类 (CLARANS)。
网格
在这些方法中,聚类形成网格状结构。这些方法的优点是所有在这些网格上进行的聚类操作都很快并且独立于数据对象的数量。例如,统计信息网格 (STING)、查询聚类 (CLIQUE)。
衡量聚类性能
关于机器学习模型,最重要的考虑因素之一是评估其性能,或者您可以说模型的质量。在监督学习算法的情况下,评估模型的质量很容易,因为我们已经为每个示例提供了标签。
另一方面,在无监督学习算法的情况下,我们没有那么幸运,因为我们处理的是未标记的数据。但我们仍然有一些指标可以使从业人员深入了解聚类变化如何根据算法发生。
在我们深入研究这些指标之前,我们必须了解这些指标仅评估模型之间的比较性能,而不是衡量模型预测的有效性。以下是一些我们可以在聚类算法上部署以衡量模型质量的指标:
轮廓分析
轮廓分析用于通过测量聚类之间的距离来检查聚类模型的质量。它基本上为我们提供了一种通过轮廓分数来评估参数(如聚类数量)的方法。此分数衡量一个聚类中的每个点与相邻聚类中的点的接近程度。
轮廓分数分析
轮廓分数的范围是 [-1, 1]。其分析如下:
+1 分数 − 接近 +1 的轮廓分数表明样本远离其相邻聚类。
0 分数 − 0 的轮廓分数表明样本位于或非常靠近分隔两个相邻聚类的决策边界。
-1 分数 &minusl -1 的轮廓分数表明样本已被分配到错误的聚类。
轮廓分数的计算可以使用以下公式进行:
𝒔𝒊𝒍𝒉𝒐𝒖𝒆𝒕𝒕𝒆 𝒔𝒄𝒐𝒓𝒆=(𝒑−𝒒)/𝐦𝐚𝐱 (𝒑,𝒒)
这里,𝑝 = 到最近聚类中点的平均距离
并且,𝑞 = 到所有点的平均聚类内距离。
戴维斯-鲍尔丁指数
DB 指数是另一个用于执行聚类算法分析的良好指标。借助 DB 指数,我们可以了解以下关于聚类模型的要点:
聚类是否彼此良好地间隔开?
聚类有多密集?
我们可以使用以下公式计算 DB 指数:
$DB=\frac{1}{n}\displaystyle\sum\limits_{i=1}^n max_{j\neq{i}}\left(\frac{\sigma_{i}+\sigma_{j}}{d(c_{i},c_{j})}\right)$这里,𝑛 = 聚类数量
σi = 聚类 𝑖 中所有点到聚类质心 𝑐𝑖 的平均距离。
DB 指数越小,聚类模型越好。
邓恩指数
它的工作原理与 DB 指数相同,但以下几点是两者不同之处:
Dunn 指数只考虑最坏情况,即距离较近的簇,而 DB 指数则考虑聚类模型中所有簇的离散度和分离度。
Dunn 指数随着性能的提高而增加,而 DB 指数在簇分布良好且密集时效果更好。
我们可以使用以下公式计算 Dunn 指数:
$D=\frac{min_{1\leq i <{j}\leq{n}}P(i,j)}{mix_{1\leq i < k \leq n}q(k)}$这里,𝑖、𝑗、𝑘 = 每个簇的索引
𝑝 = 簇间距离
q = 簇内距离
机器学习聚类算法类型
以下是最重要的和有用的机器学习聚类算法:
K 均值聚类
此聚类算法计算质心并迭代,直到找到最佳质心。它假设簇的数量已知。它也被称为扁平聚类算法。算法从数据中识别出的簇的数量在 K 均值中用“K”表示。
均值漂移算法
它是另一种用于无监督学习的强大聚类算法。与 K 均值聚类不同,它不作任何假设,因此它是一种非参数算法。
层次聚类
它是另一种无监督学习算法,用于将具有相似特征的未标记数据点分组。
我们将在后续章节中详细讨论所有这些算法。
聚类的应用
我们可以在以下领域发现聚类很有用:
数据汇总和压缩 - 聚类广泛应用于需要数据汇总、压缩和降维的领域。例如图像处理和矢量量化。
协同系统和客户细分 - 由于聚类可用于查找类似产品或相同类型的用户,因此可用于协同系统和客户细分领域。
作为其他数据挖掘任务的关键中间步骤 - 聚类分析可以生成数据的紧凑摘要,用于分类、测试、假设生成;因此,它也作为其他数据挖掘任务的关键中间步骤。
动态数据中的趋势检测 - 聚类还可以通过对相似趋势进行各种聚类来用于动态数据中的趋势检测。
社交网络分析 - 聚类可以用于社交网络分析。例如,在图像、视频或音频中生成序列。
生物数据分析 - 聚类还可以用于对图像、视频进行聚类,因此可以成功地用于生物数据分析。
聚类算法 - K 均值算法
K 均值算法简介
K 均值聚类算法计算质心并迭代,直到找到最佳质心。它假设簇的数量已知。它也被称为扁平聚类算法。算法从数据中识别出的簇的数量在 K 均值中用“K”表示。
在此算法中,数据点被分配到一个簇中,以使数据点和质心之间平方距离之和最小。需要理解的是,簇内差异越小,同一个簇内的数据点越相似。
K 均值算法的工作原理
我们可以借助以下步骤了解 K 均值聚类算法的工作原理:
步骤 1 - 首先,我们需要指定此算法需要生成的簇的数量 K。
步骤 2 - 接下来,随机选择 K 个数据点并将每个数据点分配到一个簇中。简单来说,就是根据数据点的数量对数据进行分类。
步骤 3 - 现在它将计算簇质心。
步骤 4 - 接下来,继续迭代以下操作,直到我们找到最佳质心,即数据点分配到不再更改的簇中:
4.1 - 首先,将计算数据点和质心之间平方距离之和。
4.2 - 现在,我们必须将每个数据点分配到比其他簇(质心)更近的簇。
4.3 - 最后,通过取该簇中所有数据点的平均值来计算簇的质心。
K 均值采用期望最大化方法来解决问题。期望步骤用于将数据点分配到最近的簇,最大化步骤用于计算每个簇的质心。
在使用 K 均值算法时,我们需要注意以下事项:
在使用包括 K 均值在内的聚类算法时,建议对数据进行标准化,因为此类算法使用基于距离的度量来确定数据点之间的相似性。
由于 K 均值的迭代性质和质心的随机初始化,K 均值可能会陷入局部最优,可能不会收敛到全局最优。因此,建议使用不同的质心初始化。
Python 中的实现
以下两个实现 K 均值聚类算法的示例将有助于我们更好地理解它:
示例 1
这是一个简单的示例,用于了解 k 均值的工作原理。在此示例中,我们将首先生成包含 4 个不同斑点的 2D 数据集,然后应用 k 均值算法查看结果。
首先,我们将从导入必要的包开始:
%matplotlib inline import matplotlib.pyplot as plt import seaborn as sns; sns.set() import numpy as np from sklearn.cluster import KMeans
以下代码将生成包含四个斑点的 2D 数据集:
from sklearn.datasets.samples_generator import make_blobs X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)
接下来,以下代码将帮助我们可视化数据集:
plt.scatter(X[:, 0], X[:, 1], s=20); plt.show()
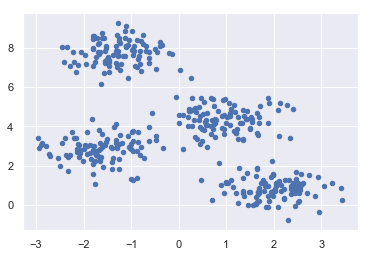
接下来,创建一个 KMeans 对象并提供簇的数量,训练模型并进行预测,如下所示:
kmeans = KMeans(n_clusters=4) kmeans.fit(X) y_kmeans = kmeans.predict(X)
现在,借助以下代码,我们可以绘制和可视化 k 均值 Python 估计器选择的簇中心:
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer') centers = kmeans.cluster_centers_ plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9); plt.show()

示例 2
让我们转向另一个示例,在这个示例中,我们将对简单的数字数据集应用 K 均值聚类。K 均值将尝试识别相似的数字,而无需使用原始标签信息。
首先,我们将从导入必要的包开始:
%matplotlib inline import matplotlib.pyplot as plt import seaborn as sns; sns.set() import numpy as np from sklearn.cluster import KMeans
接下来,从 sklearn 加载数字数据集并创建一个对象。我们还可以找到此数据集中行数和列数,如下所示:
from sklearn.datasets import load_digits digits = load_digits() digits.data.shape
输出
(1797, 64)
以上输出显示此数据集有 1797 个样本,64 个特征。
我们可以像在上面的示例 1 中一样执行聚类:
kmeans = KMeans(n_clusters=10, random_state=0) clusters = kmeans.fit_predict(digits.data) kmeans.cluster_centers_.shape
输出
(10, 64)
以上输出显示 K 均值创建了 10 个簇,64 个特征。
fig, ax = plt.subplots(2, 5, figsize=(8, 3)) centers = kmeans.cluster_centers_.reshape(10, 8, 8) for axi, center in zip(ax.flat, centers): axi.set(xticks=[], yticks=[]) axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)
输出
作为输出,我们将获得以下图像,显示 k 均值学习的簇中心。
以下代码行将学习到的簇标签与其中找到的真实标签匹配:
from scipy.stats import mode labels = np.zeros_like(clusters) for i in range(10): mask = (clusters == i) labels[mask] = mode(digits.target[mask])[0]
接下来,我们可以检查准确率,如下所示:
from sklearn.metrics import accuracy_score accuracy_score(digits.target, labels)
输出
0.7935447968836951
以上输出显示准确率约为 80%。
优点和缺点
优点
以下是 K 均值聚类算法的一些优点:
它非常容易理解和实现。
如果我们有大量变量,那么 K 均值将比层次聚类更快。
在重新计算质心时,实例可以更改簇。
与层次聚类相比,K 均值形成的簇更紧密。
缺点
以下是 K 均值聚类算法的一些缺点:
很难预测簇的数量,即 k 的值。
输出受初始输入(如簇的数量(k 的值))的强烈影响。
数据的顺序将对最终输出产生强烈影响。
它对重新缩放非常敏感。如果我们通过归一化或标准化重新缩放数据,则输出将完全改变。最终输出。
如果簇具有复杂的几何形状,则它不适合执行聚类任务。
K 均值聚类算法的应用
聚类分析的主要目标是:
从我们正在处理的数据中获得有意义的直觉。
先聚类后预测,其中将为不同的子组构建不同的模型。
为了实现上述目标,K 均值聚类表现得足够好。它可用于以下应用:
市场细分
文档聚类
图像分割
图像压缩
客户细分
分析动态数据的趋势
聚类算法 - 均值漂移算法
均值漂移算法简介
如前所述,它是另一种用于无监督学习的强大聚类算法。与 K 均值聚类不同,它不作任何假设;因此它是一种非参数算法。
均值漂移算法基本上通过将点移向数据点密度最高的位置(即簇质心)来迭代地将数据点分配到簇中。
K 均值算法和均值漂移算法的区别在于,后者不需要预先指定簇的数量,因为簇的数量将由算法根据数据确定。
均值漂移算法的工作原理
我们可以借助以下步骤了解均值漂移聚类算法的工作原理:
步骤 1 - 首先,从将数据点分配到它们自己的簇开始。
步骤 2 - 接下来,此算法将计算质心。
步骤 3 - 在此步骤中,将更新新质心位置。
步骤 4 - 现在,该过程将迭代并移动到更高密度的区域。
步骤 5 - 最后,一旦质心到达无法进一步移动的位置,它将停止。
Python 中的实现
这是一个简单的示例,用于了解均值漂移算法的工作原理。在此示例中,我们将首先生成包含 4 个不同斑点的 2D 数据集,然后应用均值漂移算法查看结果。
%matplotlib inline
import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.datasets.samples_generator import make_blobs
centers = [[3,3,3],[4,5,5],[3,10,10]]
X, _ = make_blobs(n_samples = 700, centers = centers, cluster_std = 0.5)
plt.scatter(X[:,0],X[:,1])
plt.show()
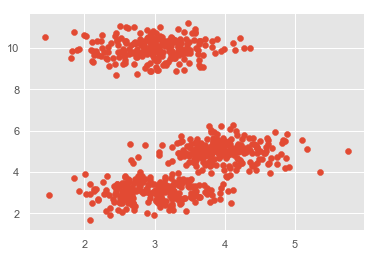
ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
colors = 10*['r.','g.','b.','c.','k.','y.','m.']
for i in range(len(X)):
plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 3)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
marker=".",color='k', s=20, linewidths = 5, zorder=10)
plt.show()
输出
[[ 2.98462798 9.9733794 10.02629344] [ 3.94758484 4.99122771 4.99349433] [ 3.00788996 3.03851268 2.99183033]] Estimated clusters: 3
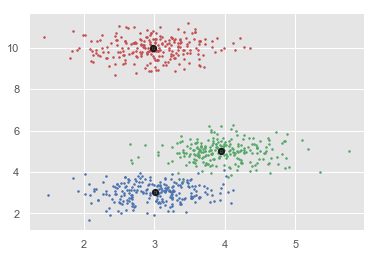
优点和缺点
优点
以下是均值漂移聚类算法的一些优点:
它不需要像 K 均值或高斯混合那样进行任何模型假设。
它还可以对具有非凸形状的复杂簇进行建模。
它只需要一个名为带宽的参数,该参数会自动确定簇的数量。
没有像 K 均值那样的局部最小值问题。
没有异常值生成的问题。
缺点
以下是均值漂移聚类算法的一些缺点:
在高维情况下,均值漂移算法效果不佳,其中簇的数量突然变化。
我们无法直接控制簇的数量,但在某些应用中,我们需要特定数量的簇。
它无法区分有意义和无意义的模式。
聚类算法 - 层次聚类
层次聚类简介
层次聚类是另一种无监督学习算法,用于将具有相似特征的未标记数据点分组在一起。层次聚类算法分为以下两类:
凝聚层次算法 − 在凝聚层次算法中,每个数据点都被视为一个单独的簇,然后依次合并或凝聚(自下而上方法)成对的簇。簇的层次结构表示为树状图或树形结构。
分裂层次算法 − 另一方面,在分裂层次算法中,所有数据点都被视为一个大的簇,聚类过程包括将一个大的簇划分为各种小的簇(自上而下方法)。
执行凝聚层次聚类的步骤
我们将解释最常用和最重要的层次聚类,即凝聚层次聚类。执行该算法的步骤如下:
步骤1 − 将每个数据点视为单个簇。因此,我们开始时将有,比如说K个簇。开始时数据点的数量也将是K。
步骤2 − 现在,在此步骤中,我们需要通过连接两个最接近的数据点来形成一个大的簇。这将导致总共有K-1个簇。
步骤3 − 现在,为了形成更多簇,我们需要连接两个最接近的簇。这将导致总共有K-2个簇。
步骤4 − 现在,为了形成一个大的簇,重复以上三个步骤,直到K变为0,即没有更多的数据点可以连接。
步骤5 − 最后,在形成一个大的簇之后,将使用树状图根据问题将其划分为多个簇。
树状图在凝聚层次聚类中的作用
正如我们在上一步中讨论的那样,树状图的作用是在形成大的簇之后开始。树状图将用于根据我们的问题将簇拆分为多个相关的簇。可以通过以下示例理解:
示例 1
为了理解,让我们从导入所需的库开始,如下所示:
%matplotlib inline import matplotlib.pyplot as plt import numpy as np
接下来,我们将绘制我们在此示例中使用的点:
X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],]) labels = range(1, 11) plt.figure(figsize=(10, 7)) plt.subplots_adjust(bottom=0.1) plt.scatter(X[:,0],X[:,1], label='True Position') for label, x, y in zip(labels, X[:, 0], X[:, 1]): plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom') plt.show()
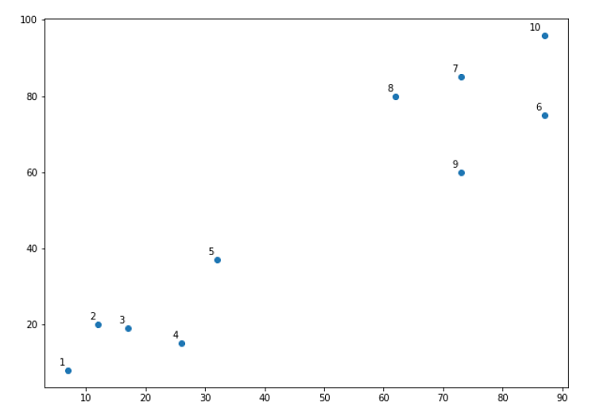
从上图可以很容易地看出,我们的数据点中有两个簇,但在现实世界的数据中,可能会有数千个簇。接下来,我们将使用Scipy库绘制数据点的树状图:
from scipy.cluster.hierarchy import dendrogram, linkage from matplotlib import pyplot as plt linked = linkage(X, 'single') labelList = range(1, 11) plt.figure(figsize=(10, 7)) dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True) plt.show()
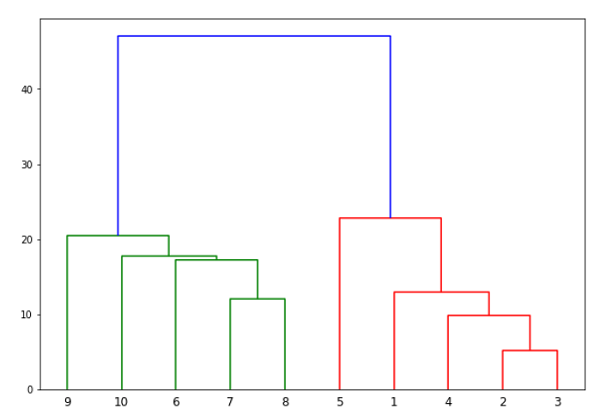
现在,一旦形成大的簇,就会选择最长的垂直距离。然后通过它绘制一条垂直线,如下面的图所示。由于水平线在两点处与蓝线相交,因此簇的数量将为两个。
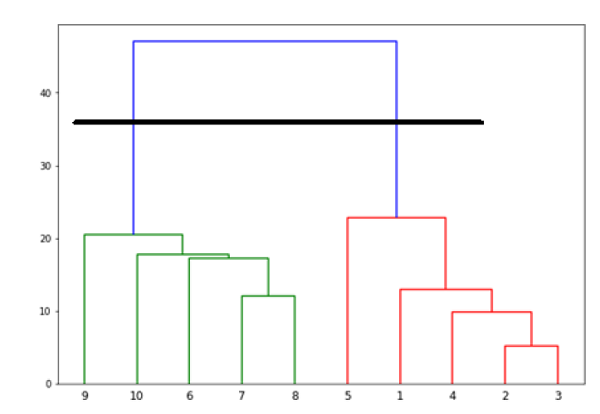
接下来,我们需要导入用于聚类的类并调用其fit_predict方法来预测簇。我们正在导入sklearn.cluster库的AgglomerativeClustering类:
from sklearn.cluster import AgglomerativeClustering cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward') cluster.fit_predict(X)
接下来,使用以下代码绘制簇:
plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')
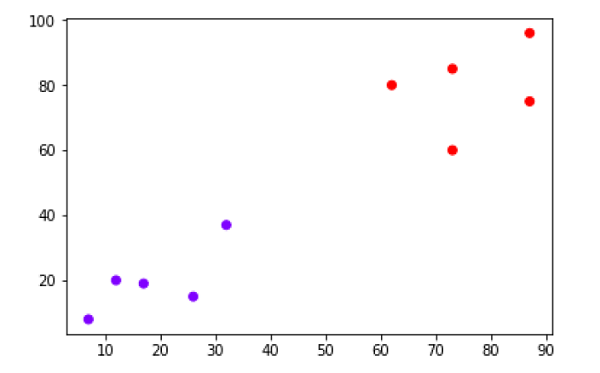
上图显示了我们数据点中的两个簇。
示例2
正如我们从上面讨论的简单示例中理解了树状图的概念,让我们继续另一个示例,其中我们使用层次聚类创建Pima印第安人糖尿病数据集中的数据点的簇:
import matplotlib.pyplot as plt import pandas as pd %matplotlib inline import numpy as np from pandas import read_csv path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8] data.shape (768, 9) data.head()
| 序号 | 怀孕次数 | 葡萄糖 | 血压 | 皮肤厚度 | 胰岛素 | BMI | 糖尿病谱系功能 | 年龄 | 类别 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))
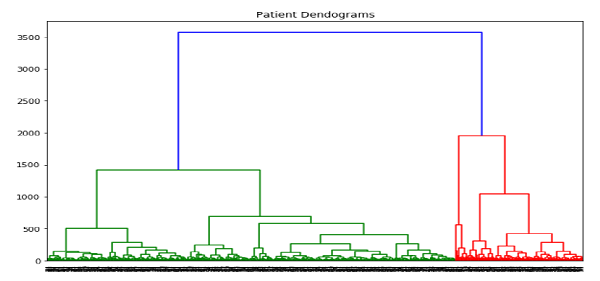
from sklearn.cluster import AgglomerativeClustering cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward') cluster.fit_predict(patient_data) plt.figure(figsize=(10, 7)) plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')
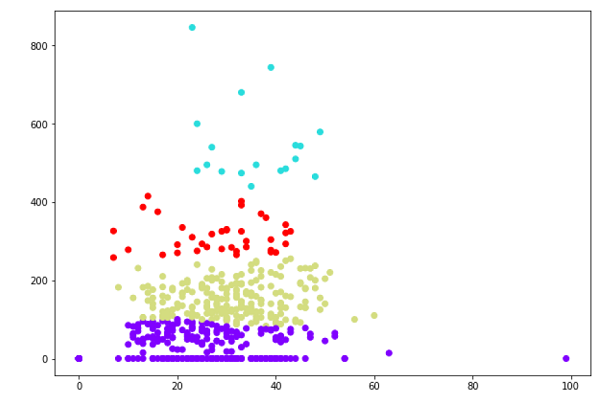
KNN算法 - 寻找最近邻
介绍
K近邻(KNN)算法是一种监督式机器学习算法,可用于分类和回归预测问题。但是,它主要用于行业中的分类预测问题。以下两个属性可以很好地定义KNN:
懒惰学习算法 − KNN是一种懒惰学习算法,因为它没有专门的训练阶段,并在分类时使用所有数据进行训练。
非参数学习算法 − KNN也是一种非参数学习算法,因为它不假设任何关于底层数据的信息。
KNN算法的工作原理
K近邻(KNN)算法使用“特征相似性”来预测新数据点的值,这进一步意味着新数据点将根据其与训练集中点的匹配程度分配一个值。我们可以通过以下步骤了解其工作原理:
步骤1 − 要实现任何算法,都需要数据集。因此,在KNN的第一步中,我们必须加载训练数据和测试数据。
步骤2 − 接下来,我们需要选择K的值,即最近的数据点。K可以是任何整数。
步骤3 − 对于测试数据中的每个点,执行以下操作:
3.1 − 使用任何方法(例如:欧几里得距离、曼哈顿距离或汉明距离)计算测试数据与训练数据每一行的距离。计算距离最常用的方法是欧几里得距离。
3.2 − 现在,根据距离值,按升序对它们进行排序。
3.3 − 接下来,它将从排序数组中选择前K行。
3.4 − 现在,它将根据这些行的最频繁类别为测试点分配一个类别。
步骤4 − 结束
示例
以下是一个示例,用于理解K的概念和KNN算法的工作原理:
假设我们有一个数据集,可以绘制如下:
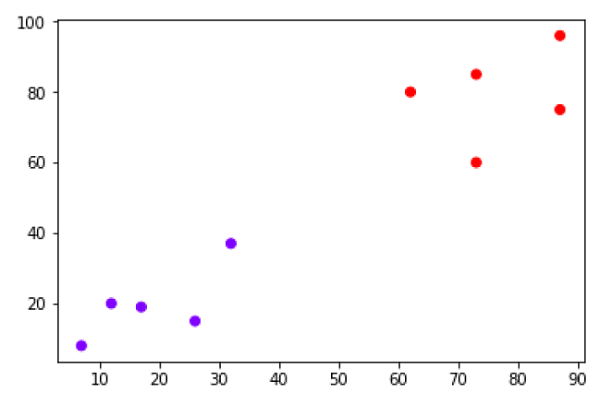
现在,我们需要将新的数据点(黑色点,在点60,60处)分类为蓝色或红色类别。我们假设K=3,即它将找到三个最近的数据点。这在下图中显示:
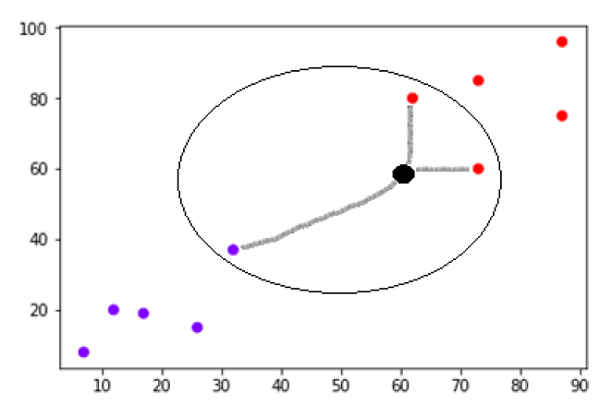
我们可以在上图中看到黑色点数据点的三个最近邻。在这三个中,有两个属于红色类别,因此黑色点也将分配到红色类别。
Python 中的实现
众所周知,K近邻(KNN)算法可用于分类和回归。以下是使用KNN作为分类器和回归器的Python代码:
KNN作为分类器
首先,从导入必要的 Python 包开始:
import numpy as np import matplotlib.pyplot as plt import pandas as pd
接下来,从其网络链接下载 iris 数据集,如下所示:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
接下来,我们需要为数据集分配列名,如下所示:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
现在,我们需要将数据集读取到 pandas 数据框中,如下所示:
dataset = pd.read_csv(path, names=headernames) dataset.head()
| 序号 | 萼片长度 | 萼片宽度 | 花瓣长度 | 花瓣宽度 | 类别 |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
数据预处理将借助以下脚本行完成:
X = dataset.iloc[:, :-1].values y = dataset.iloc[:, 4].values
接下来,我们将数据划分为训练集和测试集。以下代码将数据集划分为60%的训练数据和40%的测试数据:
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40)
接下来,将执行数据缩放,如下所示:
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test)
接下来,使用sklearn的KNeighborsClassifier类训练模型,如下所示:
from sklearn.neighbors import KNeighborsClassifier classifier = KNeighborsClassifier(n_neighbors=8) classifier.fit(X_train, y_train)
最后,我们需要进行预测。这可以通过以下脚本完成:
y_pred = classifier.predict(X_test)
接下来,打印结果,如下所示:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)
输出
Confusion Matrix:
[[21 0 0]
[ 0 16 0]
[ 0 7 16]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 21
Iris-versicolor 0.70 1.00 0.82 16
Iris-virginica 1.00 0.70 0.82 23
micro avg 0.88 0.88 0.88 60
macro avg 0.90 0.90 0.88 60
weighted avg 0.92 0.88 0.88 60
Accuracy: 0.8833333333333333
KNN作为回归器
首先,从导入必要的 Python 包开始:
import numpy as np import pandas as pd
接下来,从其网络链接下载 iris 数据集,如下所示:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
接下来,我们需要为数据集分配列名,如下所示:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
现在,我们需要将数据集读取到 pandas 数据框中,如下所示:
data = pd.read_csv(url, names=headernames) array = data.values X = array[:,:2] Y = array[:,2] data.shape output:(150, 5)
接下来,从sklearn导入KNeighborsRegressor以拟合模型:
from sklearn.neighbors import KNeighborsRegressor knnr = KNeighborsRegressor(n_neighbors=10) knnr.fit(X, y)
最后,我们可以找到MSE,如下所示:
print ("The MSE is:",format(np.power(y-knnr.predict(X),2).mean()))
输出
The MSE is: 0.12226666666666669
KNN的优缺点
优点
这是一个非常容易理解和解释的算法。
它对非线性数据非常有用,因为此算法不对数据做出任何假设。
它是一种通用的算法,因为我们可以将其用于分类和回归。
它具有相对较高的准确性,但与KNN相比,还有更好的监督学习模型。
缺点
它在计算上是一个稍微昂贵的算法,因为它存储所有训练数据。
与其他监督学习算法相比,需要较高的内存存储。
如果N很大,预测速度会很慢。
它对数据的尺度和无关特征非常敏感。
KNN的应用
以下是一些KNN可以成功应用的领域:
银行系统
KNN可用于银行系统中预测个人是否适合贷款审批?该个人是否具有与违约者相似的特征?
计算信用评级
KNN算法可用于通过与具有相似特征的人进行比较来查找个人的信用评级。
政治
借助KNN算法,我们可以将潜在选民分类为不同的类别,例如“将投票”、“将不投票”、“将投票给国大党”、“将投票给人民党”。
KNN算法可用于的其他领域包括语音识别、手写识别、图像识别和视频识别。
机器学习 - 性能指标
我们可以使用各种指标来评估机器学习算法的性能,包括分类算法和回归算法。我们必须仔细选择用于评估机器学习性能的指标,因为:
机器学习算法的性能如何衡量和比较将完全取决于您选择的指标。
您如何权衡结果中各种特征的重要性将完全受您选择的指标影响。
分类问题的性能指标
我们在前面的章节中讨论了分类及其算法。在这里,我们将讨论可用于评估分类问题预测的各种性能指标。
混淆矩阵
它是衡量分类问题性能的最简单方法,其中输出可以是两种或多种类型的类别。混淆矩阵不过是一个二维表,即“实际”和“预测”,此外,这两个维度都有“真阳性 (TP)”、“真阴性 (TN)”、“假阳性 (FP)”、“假阴性 (FN)”如下所示 -
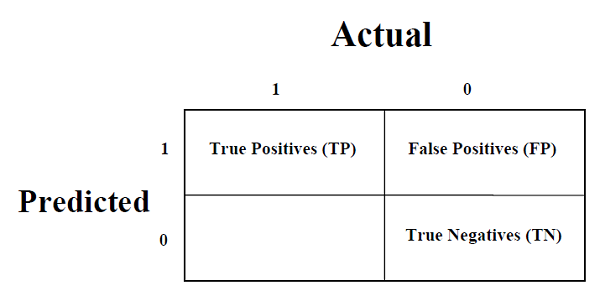
与混淆矩阵相关的术语解释如下:
真阳性 (TP) - 当数据点的实际类别和预测类别均为 1 时。
真阴性 (TN) - 当数据点的实际类别和预测类别均为 0 时。
假阳性 (FP) - 当数据点的实际类别为 0 且预测类别为 1 时。
假阴性 (FN) - 当数据点的实际类别为 1 且预测类别为 0 时。
我们可以使用sklearn.metrics的confusion_matrix函数来计算分类模型的混淆矩阵。
分类准确率
它是分类算法最常见的性能指标。可以将其定义为正确预测的数量与所有预测数量的比率。我们可以使用以下公式通过混淆矩阵轻松计算它:
$Accuracy =\frac{TP+TN}{𝑇𝑃+𝐹𝑃+𝐹𝑁+𝑇𝑁}$我们可以使用sklearn.metrics的accuracy_score函数来计算分类模型的准确率。
分类报告
此报告包含精确率、召回率、F1分数和支持度的分数。解释如下:
精确率
精确率,在文档检索中使用,可以定义为我们的 ML 模型返回的正确文档的数量。我们可以很容易地通过混淆矩阵使用以下公式计算它 -
$Precision=\frac{TP}{TP+FP}$召回率或灵敏度
召回率可以定义为我们的 ML 模型返回的阳性数量。我们可以很容易地通过混淆矩阵使用以下公式计算它 -
$Recall =\frac{TP}{TP+FN}$特异性
特异性,与召回率相反,可以定义为我们的 ML 模型返回的阴性数量。我们可以很容易地通过混淆矩阵使用以下公式计算它 -
$Specificity =\frac{TN}{TN+FP}$支持度
支持度可以定义为位于目标值每个类别中的真实响应样本的数量。
F1分数
此分数将提供精确率和召回率的调和平均值。在数学上,F1分数是精确率和召回率的加权平均值。F1的最佳值为1,最差值为0。我们可以使用以下公式计算F1分数:
𝑭𝟏 = 𝟐 ∗ (𝒑𝒓𝒆𝒄𝒊𝒔𝒊𝒐𝒏 ∗ 𝒓𝒆𝒄𝒂𝒍𝒍) / (𝒑𝒓𝒆𝒄𝒊𝒔𝒊𝒐𝒏 + 𝒓𝒆𝒄𝒂𝒍𝒍)
F1分数对精确率和召回率具有相等的相对贡献。
我们可以使用sklearn.metrics的classification_report函数获取分类模型的分类报告。
AUC(ROC曲线下面积)
AUC(曲线下面积)-ROC(受试者工作特征)是一种用于分类问题的性能指标,它基于不同的阈值。顾名思义,ROC是一条概率曲线,而AUC衡量的是可分离性。简单来说,AUC-ROC指标可以告诉我们模型区分不同类别的能力。AUC越高,模型越好。
在数学上,它可以通过绘制TPR(真正率),即灵敏度或召回率,与FPR(假正率),即1-特异度,在不同阈值下的曲线来创建。下图显示了ROC,AUC,其中y轴为TPR,x轴为FPR:
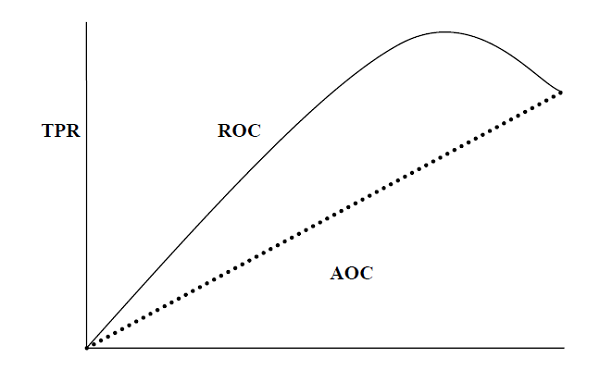
我们可以使用sklearn.metrics中的roc_auc_score函数来计算AUC-ROC。
LOGLOSS(对数损失)
它也称为逻辑回归损失或交叉熵损失。它基本上定义在概率估计上,并衡量分类模型的性能,其中输入是一个介于0和1之间的概率值。通过将其与准确率进行区分,可以更清楚地理解它。我们知道准确率是我们模型中预测值等于实际值的预测次数,而对数损失是我们预测的不确定性,基于它与实际标签的差异程度。借助对数损失值,我们可以更准确地了解模型的性能。我们可以使用sklearn.metrics中的log_loss函数来计算对数损失。
示例
下面是一个简单的Python示例,它可以让我们了解如何在二元分类模型上使用上述性能指标:
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
X_actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
Y_predic = [1, 0, 1, 1, 1, 0, 1, 1, 0, 0]
results = confusion_matrix(X_actual, Y_predic)
print ('Confusion Matrix :')
print(results)
print ('Accuracy Score is',accuracy_score(X_actual, Y_predic))
print ('Classification Report : ')
print (classification_report(X_actual, Y_predic))
print('AUC-ROC:',roc_auc_score(X_actual, Y_predic))
print('LOGLOSS Value is',log_loss(X_actual, Y_predic))
输出
Confusion Matrix :
[[3 3]
[1 3]]
Accuracy Score is 0.6
Classification Report :
precision recall f1-score support
0 0.75 0.50 0.60 6
1 0.50 0.75 0.60 4
micro avg 0.60 0.60 0.60 10
macro avg 0.62 0.62 0.60 10
weighted avg 0.65 0.60 0.60 10
AUC-ROC: 0.625
LOGLOSS Value is 13.815750437193334
回归问题的性能指标
我们在前面的章节中讨论了回归及其算法。在这里,我们将讨论可用于评估回归问题预测结果的各种性能指标。
平均绝对误差(MAE)
这是回归问题中最简单的误差指标。它基本上是预测值和实际值之间绝对差值的平均和。简单来说,通过MAE,我们可以了解预测的错误程度。MAE不指示模型的方向,即没有关于模型的欠拟合或过拟合的指示。计算MAE的公式如下:
$MAE = \frac{1}{n}\sum|Y -\hat{Y}|$这里,𝑌=实际输出值
以及$\hat{Y}$=预测输出值。
我们可以使用sklearn.metrics中的mean_absolute_error函数来计算MAE。
均方误差(MSE)
MSE类似于MAE,但唯一的区别在于它在对所有差值求和之前,先对实际输出值和预测输出值之间的差值进行平方,而不是使用绝对值。在下面的等式中可以注意到差异:
$MSE = \frac{1}{n}\sum(Y -\hat{Y})^2$这里,𝑌=实际输出值
以及$\hat{Y}$ = 预测输出值。
我们可以使用sklearn.metrics中的mean_squared_error函数来计算MSE。
R平方(R2)
R平方指标通常用于解释目的,并提供一组预测输出值与实际输出值拟合优度的指示。下面的公式将帮助我们理解它:
$R^{2} = 1 -\frac{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\hat{Y_{i}})^2}{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\bar{Y_i})^2}$在上式中,分子是MSE,分母是𝑌值的方差。
我们可以使用sklearn.metrics中的r2_score函数来计算R平方值。
示例
下面是一个简单的Python示例,它可以让我们了解如何在回归模型上使用上述性能指标:
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
X_actual = [5, -1, 2, 10]
Y_predic = [3.5, -0.9, 2, 9.9]
print ('R Squared =',r2_score(X_actual, Y_predic))
print ('MAE =',mean_absolute_error(X_actual, Y_predic))
print ('MSE =',mean_squared_error(X_actual, Y_predic))
输出
R Squared = 0.9656060606060606 MAE = 0.42499999999999993 MSE = 0.5674999999999999
机器学习 - 自动工作流
介绍
为了成功地执行并产生结果,机器学习模型必须自动化一些标准的工作流。自动化这些标准工作流的过程可以通过Scikit-learn管道来完成。从数据科学家的角度来看,管道是一个通用但非常重要的概念。它基本上允许数据从其原始格式流向一些有用的信息。可以通过下图了解管道的运作方式:
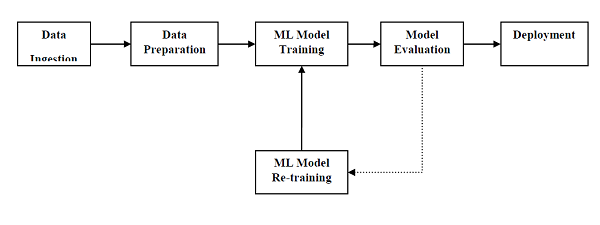
ML管道的模块如下:
数据摄取 - 顾名思义,它是导入数据以用于ML项目的过程。数据可以实时或批量地从单个或多个系统中提取。这是最具挑战性的步骤之一,因为数据的质量会影响整个ML模型。
数据准备 - 导入数据后,我们需要准备数据以用于我们的ML模型。数据预处理是数据准备中最重要的技术之一。
ML模型训练 - 下一步是训练我们的ML模型。我们有各种ML算法,如监督学习、无监督学习、强化学习,可以从数据中提取特征并进行预测。
模型评估 - 接下来,我们需要评估ML模型。在AutoML管道的情况下,ML模型可以通过各种统计方法和业务规则进行评估。
ML模型再训练 - 在AutoML管道的情况下,第一个模型不一定是最好的模型。第一个模型被视为基线模型,我们可以重复训练它以提高模型的准确性。
部署 - 最后,我们需要部署模型。此步骤涉及将模型应用并迁移到业务运营以供其使用。
ML管道伴随的挑战
为了创建ML管道,数据科学家面临着许多挑战。这些挑战分为以下三类:
数据质量
任何ML模型的成功都严重依赖于数据的质量。如果我们提供给ML模型的数据不准确、不可靠和稳健,那么我们将得到错误或误导性的输出。
数据可靠性
与ML管道相关的另一个挑战是我们提供给ML模型的数据的可靠性。众所周知,数据科学家可以从各种来源获取数据,但为了获得最佳结果,必须确保数据源是可靠和可信的。
数据可访问性
为了从ML管道中获得最佳结果,数据本身必须是可访问的,这需要对数据进行整合、清洗和整理。由于数据可访问性属性,元数据将使用新标签进行更新。
ML管道和数据准备建模
数据泄漏,从训练数据集到测试数据集,是数据科学家在准备ML模型数据时需要处理的一个重要问题。通常,在数据准备时,数据科学家会在学习之前对整个数据集使用标准化或归一化等技术。但是,这些技术无法帮助我们防止数据泄漏,因为训练数据集会受到测试数据集中数据规模的影响。
通过使用ML管道,我们可以防止这种数据泄漏,因为管道确保数据准备(如标准化)仅限于交叉验证过程的每个折叠。
示例
以下是一个Python示例,演示数据准备和模型评估工作流。为此,我们使用Sklearn中的Pima印第安人糖尿病数据集。首先,我们将创建一个标准化数据的管道。然后创建一个线性判别分析模型,最后使用10折交叉验证评估管道。
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values
接下来,我们将使用以下代码创建一个管道:
estimators = []
estimators.append(('standardize', StandardScaler()))
estimators.append(('lda', LinearDiscriminantAnalysis()))
model = Pipeline(estimators)
最后,我们将评估此管道并输出其准确率,如下所示:
kfold = KFold(n_splits=20, random_state=7) results = cross_val_score(model, X, Y, cv=kfold) print(results.mean())
输出
0.7790148448043184
上述输出是数据集上设置的准确率摘要。
ML管道和特征提取建模
数据泄漏也可能发生在ML模型的特征提取步骤中。因此,特征提取过程也应受到限制,以停止训练数据集中的数据泄漏。与数据准备一样,通过使用ML管道,我们也可以防止这种数据泄漏。FeatureUnion是ML管道提供的一个工具,可用于此目的。
示例
以下是一个Python示例,演示特征提取和模型评估工作流。为此,我们使用Sklearn中的Pima印第安人糖尿病数据集。
首先,将使用PCA(主成分分析)提取3个特征。然后,将使用统计分析提取6个特征。在特征提取之后,将使用
FeatureUnion工具组合多个特征选择和提取过程的结果。最后,将创建一个逻辑回归模型,并使用10折交叉验证评估管道。
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.pipeline import Pipeline from sklearn.pipeline import FeatureUnion from sklearn.linear_model import LogisticRegression from sklearn.decomposition import PCA from sklearn.feature_selection import SelectKBest
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values
接下来,将创建特征联合,如下所示:
features = []
features.append(('pca', PCA(n_components=3)))
features.append(('select_best', SelectKBest(k=6)))
feature_union = FeatureUnion(features)
接下来,将使用以下脚本行创建管道:
estimators = []
estimators.append(('feature_union', feature_union))
estimators.append(('logistic', LogisticRegression()))
model = Pipeline(estimators)
最后,我们将评估此管道并输出其准确率,如下所示:
kfold = KFold(n_splits=20, random_state=7) results = cross_val_score(model, X, Y, cv=kfold) print(results.mean())
输出
0.7789811066126855
上述输出是数据集上设置的准确率摘要。
改进机器学习模型的性能
集成方法性能改进
集成方法可以通过组合多个模型来提高机器学习结果。基本上,集成模型由几个单独训练的监督学习模型组成,并且它们的预测结果以各种方式合并,以实现比单个模型更好的预测性能。集成方法可以分为以下两组:
顺序集成方法
顾名思义,在这种集成方法中,基学习器是按顺序生成的。此类方法的动机是利用基学习器之间的依赖关系。
并行集成方法
顾名思义,在这种集成方法中,基学习器是并行生成的。此类方法的动机是利用基学习器之间的独立性。
集成学习方法
以下是最流行的集成学习方法,即组合不同模型预测的方法:
Bagging
术语Bagging也称为Bootstrap聚合。在Bagging方法中,集成模型试图通过组合在随机生成的训练样本上训练的各个模型的预测来提高预测准确性和降低模型方差。集成模型的最终预测将通过计算所有单个估计器的预测的平均值来给出。Bagging方法的一个最佳示例是随机森林。
Boosting
在Boosting方法中,构建集成模型的主要原理是通过按顺序训练每个基模型估计器来增量构建它。顾名思义,它基本上将多个弱基学习器(在训练数据的多个迭代中按顺序训练)组合起来以构建强大的集成。在训练弱基学习器期间,会为之前被错误分类的学习器分配更高的权重。Boosting方法的示例是AdaBoost。
投票
在这个集成学习模型中,构建了多种不同类型的模型,并使用一些简单的统计方法(如计算平均值或中位数等)来组合预测结果。该预测将作为训练的额外输入以进行最终预测。
Bagging集成算法
以下是三种Bagging集成算法:
Bagged决策树
众所周知,Bagging 集成方法对于方差较大的算法效果很好,其中决策树算法是最佳选择之一。在下面的 Python 示例中,我们将使用 sklearn 的 BaggingClassifier 函数和 DecisionTreeClasifier(一种分类和回归树算法)在 Pima 印第安人糖尿病数据集上构建 Bagging 决策树集成模型。
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import BaggingClassifier from sklearn.tree import DecisionTreeClassifier
现在,我们需要像之前示例中那样加载 Pima 糖尿病数据集 -
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,如下所示,为 10 折交叉验证提供输入 -
seed = 7 kfold = KFold(n_splits=10, random_state=seed) cart = DecisionTreeClassifier()
我们需要提供要构建的树的数量。这里我们将构建 150 棵树 -
num_trees = 150
接下来,使用以下脚本构建模型 -
model = BaggingClassifier(base_estimator=cart, n_estimators=num_trees, random_state=seed)
计算并打印结果,如下所示 -
results = cross_val_score(model, X, Y, cv=kfold) print(results.mean())
输出
0.7733766233766234
上面的输出表明,我们 Bagging 决策树分类器模型的准确率约为 77%。
随机森林
它是 Bagging 决策树的扩展。对于单个分类器,训练数据集的样本是带放回地采样的,但树的构建方式可以降低它们之间的相关性。此外,在构建每棵树时,会考虑特征的随机子集来选择每个分割点,而不是贪婪地选择最佳分割点。
在下面的 Python 示例中,我们将使用 sklearn 的 RandomForestClassifier 类在 Pima 印第安人糖尿病数据集上构建 Bagging 随机森林集成模型。
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import RandomForestClassifier
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,如下所示,为 10 折交叉验证提供输入 -
seed = 7 kfold = KFold(n_splits=10, random_state=seed)
我们需要提供要构建的树的数量。这里我们将构建 150 棵树,并且分割点从 5 个特征中选择 -
num_trees = 150 max_features = 5
接下来,使用以下脚本构建模型 -
model = RandomForestClassifier(n_estimators=num_trees, max_features=max_features)
计算并打印结果,如下所示 -
results = cross_val_score(model, X, Y, cv=kfold) print(results.mean())
输出
0.7629357484620642
上面的输出表明,我们 Bagging 随机森林分类器模型的准确率约为 76%。
极端随机树 (Extra Trees)
它是 Bagging 决策树集成方法的另一种扩展。在这种方法中,随机树是从训练数据集的样本中构建的。
在下面的 Python 示例中,我们将使用 sklearn 的 ExtraTreesClassifier 类在 Pima 印第安人糖尿病数据集上构建极端随机树集成模型。
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import ExtraTreesClassifier
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,如下所示,为 10 折交叉验证提供输入 -
seed = 7 kfold = KFold(n_splits=10, random_state=seed)
我们需要提供要构建的树的数量。这里我们将构建 150 棵树,并且分割点从 5 个特征中选择 -
num_trees = 150 max_features = 5
接下来,使用以下脚本构建模型 -
model = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)
计算并打印结果,如下所示 -
results = cross_val_score(model, X, Y, cv=kfold) print(results.mean())
输出
0.7551435406698566
上面的输出表明,我们 Bagging 极端随机树分类器模型的准确率约为 75.5%。
Boosting 集成算法
以下是两种最常见的 Boosting 集成算法 -
AdaBoost
它是最成功的 Boosting 集成算法之一。该算法的主要关键在于它们赋予数据集中实例权重的方式。因此,算法在构建后续模型时需要减少对实例的关注。
在下面的 Python 示例中,我们将使用 sklearn 的 AdaBoostClassifier 类在 Pima 印第安人糖尿病数据集上构建用于分类的 AdaBoost 集成模型。
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import AdaBoostClassifier
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,如下所示,为 10 折交叉验证提供输入 -
seed = 5 kfold = KFold(n_splits=10, random_state=seed)
我们需要提供要构建的树的数量。这里我们将构建 150 棵树,并且分割点从 5 个特征中选择 -
num_trees = 50
接下来,使用以下脚本构建模型 -
model = AdaBoostClassifier(n_estimators=num_trees, random_state=seed)
计算并打印结果,如下所示 -
results = cross_val_score(model, X, Y, cv=kfold) print(results.mean())
输出
0.7539473684210527
上面的输出表明,我们的 AdaBoost 分类器集成模型的准确率约为 75%。
随机梯度提升 (Stochastic Gradient Boosting)
它也被称为梯度提升机 (Gradient Boosting Machines)。在下面的 Python 示例中,我们将使用 sklearn 的 GradientBoostingClassifier 类在 Pima 印第安人糖尿病数据集上构建用于分类的随机梯度提升集成模型。
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.ensemble import GradientBoostingClassifier
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,如下所示,为 10 折交叉验证提供输入 -
seed = 5 kfold = KFold(n_splits=10, random_state=seed)
我们需要提供要构建的树的数量。这里我们将构建 150 棵树,并且分割点从 5 个特征中选择 -
num_trees = 50
接下来,使用以下脚本构建模型 -
model = GradientBoostingClassifier(n_estimators=num_trees, random_state=seed)
计算并打印结果,如下所示 -
results = cross_val_score(model, X, Y, cv=kfold) print(results.mean())
输出
0.7746582365003418
上面的输出表明,我们的梯度提升分类器集成模型的准确率约为 77.5%。
投票集成算法 (Voting Ensemble Algorithms)
如前所述,投票首先从训练数据集中创建两个或多个独立模型,然后投票分类器将封装模型,并在需要新数据时获取子模型预测结果的平均值。
在下面的 Python 示例中,我们将使用 sklearn 的 VotingClassifier 类在 Pima 印第安人糖尿病数据集上构建投票集成模型用于分类。我们将逻辑回归、决策树分类器和 SVM 的预测结果组合在一起,用于解决分类问题,如下所示 -
首先,导入所需的包,如下所示:
from pandas import read_csv from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC from sklearn.ensemble import VotingClassifier
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,如下所示,为 10 折交叉验证提供输入 -
kfold = KFold(n_splits=10, random_state=7)
接下来,我们需要创建子模型,如下所示 -
estimators = []
model1 = LogisticRegression()
estimators.append(('logistic', model1))
model2 = DecisionTreeClassifier()
estimators.append(('cart', model2))
model3 = SVC()
estimators.append(('svm', model3))
现在,通过组合上面创建的子模型的预测结果,创建投票集成模型。
ensemble = VotingClassifier(estimators) results = cross_val_score(ensemble, X, Y, cv=kfold) print(results.mean())
输出
0.7382262474367738
上面的输出表明,我们的投票分类器集成模型的准确率约为 74%。
改进机器学习模型的性能(续…)
通过算法调优提高性能
众所周知,机器学习模型是以参数化的方式构建的,其行为可以针对特定问题进行调整。算法调优意味着找到这些参数的最佳组合,以便提高机器学习模型的性能。此过程有时称为超参数优化,算法本身的参数称为超参数,而机器学习算法找到的系数称为参数。
这里,我们将讨论 Python Scikit-learn 提供的一些算法参数调优方法。
网格搜索参数调优 (Grid Search Parameter Tuning)
这是一种参数调优方法。这种方法的工作关键在于,它对网格中指定的算法参数的每个可能组合进行系统地构建和评估模型。因此,我们可以说这种算法具有搜索的特性。
示例
在下面的 Python 示例中,我们将使用 sklearn 的 GridSearchCV 类在 Pima 印第安人糖尿病数据集上执行网格搜索,以评估岭回归算法的各种 alpha 值。
首先,导入所需的包,如下所示:
import numpy from pandas import read_csv from sklearn.linear_model import Ridge from sklearn.model_selection import GridSearchCV
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,评估各种 alpha 值,如下所示 -
alphas = numpy.array([1,0.1,0.01,0.001,0.0001,0]) param_grid = dict(alpha=alphas)
现在,我们需要将网格搜索应用于我们的模型 -
model = Ridge() grid = GridSearchCV(estimator=model, param_grid=param_grid) grid.fit(X, Y)
使用以下脚本行打印结果 -
print(grid.best_score_) print(grid.best_estimator_.alpha)
输出
0.2796175593129722 1.0
上面的输出提供了最佳得分以及网格中获得该得分的参数集。在这种情况下,alpha 值为 1.0。
随机搜索参数调优 (Random Search Parameter Tuning)
这是一种参数调优方法。这种方法的工作关键在于,它从随机分布中对算法参数进行采样,并进行固定次数的迭代。
示例
在下面的 Python 示例中,我们将使用 sklearn 的 RandomizedSearchCV 类在 Pima 印第安人糖尿病数据集上执行随机搜索,以评估岭回归算法在 0 到 1 之间的不同 alpha 值。
首先,导入所需的包,如下所示:
import numpy from pandas import read_csv from scipy.stats import uniform from sklearn.linear_model import Ridge from sklearn.model_selection import RandomizedSearchCV
现在,我们需要加载Pima糖尿病数据集,就像在前面的示例中所做的那样:
path = r"C:\pima-indians-diabetes.csv" headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class'] data = read_csv(path, names=headernames) array = data.values X = array[:,0:8] Y = array[:,8]
接下来,评估岭回归算法上的各种 alpha 值,如下所示 -
param_grid = {'alpha': uniform()}
model = Ridge()
random_search = RandomizedSearchCV(estimator=model, param_distributions=param_grid, n_iter=50,
random_state=7)
random_search.fit(X, Y)
使用以下脚本行打印结果 -
print(random_search.best_score_) print(random_search.best_estimator_.alpha)
输出
0.27961712703051084 0.9779895119966027 0.9779895119966027
上面的输出提供了最佳得分,类似于网格搜索。