分类 - 简介

上一页
下一页

分类简介

分类可以定义为从观察值或给定数据点预测类别或范畴的过程。分类输出可以采用“黑色”或“白色”或“垃圾邮件”或“非垃圾邮件”等形式。

在数学上，分类是从输入变量 (X) 到输出变量 (Y) 的近似映射函数 (f) 的任务。它基本上属于监督机器学习，其中目标也与输入数据集一起提供。

分类问题的示例可以是电子邮件中的垃圾邮件检测。输出只有两种类别，“垃圾邮件”和“非垃圾邮件”；因此，这是一种二元分类。

为了实现这种分类，我们首先需要训练分类器。对于此示例，“垃圾邮件”和“非垃圾邮件”电子邮件将用作训练数据。成功训练分类器后，它可用于检测未知电子邮件。

分类中的学习器类型

在分类问题方面，我们有两种类型的学习器 -

懒惰学习器

顾名思义，这种学习器在存储训练数据后等待测试数据出现。只有在获得测试数据后才会进行分类。它们在训练上花费的时间较少，但在预测上花费的时间较多。懒惰学习器的示例包括 K 最近邻和基于案例的推理。

急切学习器

与懒惰学习器相反，急切学习器在存储训练数据后构建分类模型，而无需等待测试数据出现。它们在训练上花费的时间更多，但在预测上花费的时间更少。急切学习器的示例包括决策树、朴素贝叶斯和人工神经网络 (ANN)。

在 Python 中构建分类器

Scikit-learn 是一个用于机器学习的 Python 库，可用于在 Python 中构建分类器。在 Python 中构建分类器的步骤如下 -

步骤 1：导入必要的 Python 包

要使用 scikit-learn 构建分类器，我们需要导入它。我们可以使用以下脚本导入它 -

import sklearn

步骤 2：导入数据集

导入必要的包后，我们需要一个数据集来构建分类预测模型。我们可以从 sklearn 数据集中导入它，也可以根据我们的需要使用其他数据集。我们将使用 sklearn 的威斯康星州乳腺癌诊断数据库。我们可以借助以下脚本导入它 -

from sklearn.datasets import load_breast_cancer

以下脚本将加载数据集；

data = load_breast_cancer()

我们还需要整理数据，这可以通过以下脚本完成 -

label_names = data['target_names']
   labels = data['target']
   feature_names = data['feature_names']
   features = data['data']

以下命令将打印标签的名称，在我们的数据库情况下为“恶性”和“良性”。

print(label_names)

上述命令的输出是标签的名称 -

['malignant' 'benign']

这些标签映射到二进制值 0 和 1。恶性癌症由 0 表示，良性癌症由 1 表示。

这些标签的特征名称和特征值可以通过以下命令查看 -

print(feature_names[0])

上述命令的输出是标签 0 即恶性癌症的特征名称 -

mean radius

类似地，标签的特征名称可以如下生成 -

print(feature_names[1])

上述命令的输出是标签 1 即良性癌症的特征名称 -

mean texture

我们可以通过以下命令打印这些标签的特征 -

print(features[0])

这将给出以下输出 -

[
   1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
   1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
   6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
   1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
   4.601e-01 1.189e-01
]

我们可以通过以下命令打印这些标签的特征 -

print(features[1])

这将给出以下输出 -

[
   2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
   7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
   5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
   2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
   2.750e-01 8.902e-02
]

步骤 3：将数据组织成训练集和测试集

由于我们需要在未见过的数据上测试我们的模型，因此我们将数据集分成两部分：训练集和测试集。我们可以使用 sklearn python 包的 train_test_split() 函数将数据拆分为数据集。以下命令将导入该函数 -

from sklearn.model_selection import train_test_split

现在，下一个命令将数据拆分为训练数据和测试数据。在此示例中，我们使用 40% 的数据进行测试，60% 的数据进行训练 -

train, test, train_labels, test_labels = train_test_split(
   features,labels,test_size = 0.40, random_state = 42
)

步骤 4：模型评估

将数据分成训练集和测试集后，我们需要构建模型。我们将使用朴素贝叶斯算法来实现此目的。以下命令将导入 GaussianNB 模块 -

from sklearn.naive_bayes import GaussianNB

现在，初始化模型如下 -

gnb = GaussianNB()

接下来，借助以下命令，我们可以训练模型 -

model = gnb.fit(train, train_labels)

现在，出于评估目的，我们需要进行预测。这可以通过使用 predict() 函数来完成，如下所示 -

preds = gnb.predict(test)
print(preds)

这将给出以下输出 -

[
   1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1
   0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1
   1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0
   0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1
   1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 
   1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 
   1

]

输出中的 0 和 1 的上述序列是恶性和良性肿瘤类别的预测值。

步骤 5：查找准确率

我们可以通过比较两个数组（即 test_labels 和 preds）来找到上一步中构建的模型的准确率。我们将使用 accuracy_score() 函数来确定准确率。

from sklearn.metrics import accuracy_score
   print(accuracy_score(test_labels,preds))
   0.951754385965

上述输出表明朴素贝叶斯分类器的准确率为 95.17%。

分类评估指标

即使您完成了机器学习应用程序或模型的实施，工作也尚未完成。我们必须找出我们的模型有多有效？可能有不同的评估指标，但我们必须仔细选择它，因为指标的选择会影响如何衡量和比较机器学习算法的性能。

以下是您可以根据您的数据集和问题类型选择的几个重要的分类评估指标 -

混淆矩阵

这是衡量分类问题性能的最简单方法，其中输出可以是两种或多种类型的类别。混淆矩阵不过是一个二维表，即“实际”和“预测”，此外，这两个维度都有“真阳性 (TP)”、“真阴性 (TN)”、“假阳性 (FP)”、“假阴性 (FN)”如下所示 -

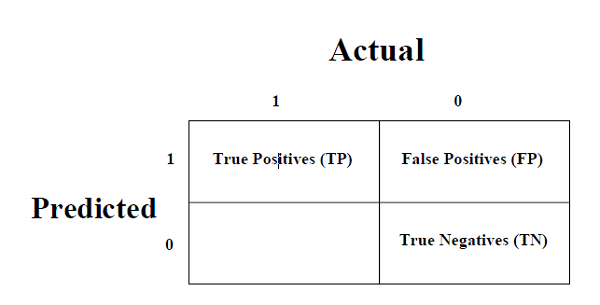
Actual

与混淆矩阵相关的术语的解释如下 -

  • **真阳性 (TP)** - 数据点的实际类别和预测类别均为 1 的情况。

  • **真阴性 (TN)** - 数据点的实际类别和预测类别均为 0 的情况。

  • **假阳性 (FP)** - 数据点的实际类别为 0，预测类别为 1 的情况。

  • **假阴性 (FN)** - 数据点的实际类别为 1，预测类别为 0 的情况。

我们可以借助 sklearn 的 confusion_matrix() 函数找到混淆矩阵。借助以下脚本，我们可以找到上面构建的二元分类器的混淆矩阵 -

from sklearn.metrics import confusion_matrix

输出

[
   [ 73   7]
   [  4 144]
]

准确率

可以将其定义为我们的机器学习模型做出的正确预测的数量。我们可以很容易地通过以下公式用混淆矩阵计算它 -

$$𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦=\frac{𝑇𝑃+𝑇𝑁}{𝑇𝑃+𝐹𝑃+𝐹𝑁+𝑇𝑁}$$

对于上面构建的二元分类器，TP + TN = 73 + 144 = 217 且 TP + FP + FN + TN = 73 + 7 + 4 + 144 = 228。

因此，准确率 = 217/228 = 0.951754385965，与我们在创建二元分类器后计算的结果相同。

精确率

精确率，用于文档检索，可以定义为我们的机器学习模型返回的正确文档的数量。我们可以很容易地通过以下公式用混淆矩阵计算它 -

$$𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛=\frac{𝑇𝑃}{𝑇𝑃+FP}$$

对于上面构建的二元分类器，TP = 73 且 TP + FP = 73 + 7 = 80。

因此，精确率 = 73/80 = 0.915

召回率或灵敏度

召回率可以定义为我们的机器学习模型返回的阳性数量。我们可以很容易地通过以下公式用混淆矩阵计算它 -

$$𝑅𝑒𝑐𝑎𝑙𝑙=\frac{𝑇𝑃}{𝑇𝑃+FN}$$

对于上面构建的二元分类器，TP = 73 且 TP + FN = 73 + 4 = 77。

因此，精确率 = 73/77 = 0.94805

特异性

与召回率相反，特异性可以定义为我们的机器学习模型返回的阴性数量。我们可以很容易地通过以下公式用混淆矩阵计算它 -

$$𝑆𝑝𝑒𝑐𝑖𝑓𝑖𝑐𝑖𝑡𝑦=\frac{𝑇N}{𝑇N+FP}$$

对于上面构建的二元分类器，TN = 144 且 TN + FP = 144 + 7 = 151。

因此，精确率 = 144/151 = 0.95364

各种机器学习分类算法

以下是几个重要的机器学习分类算法 -

  • 逻辑回归

  • 支持向量机 (SVM)

  • 决策树

  • 朴素贝叶斯

  • 随机森林

我们将在后面的章节中详细讨论所有这些分类算法。

应用

以下是分类算法的一些最重要的应用 -

  • 语音识别

  • 手写识别

  • 生物识别身份识别

  • 文档分类

打印页面
上一页
下一页
广告

© . All rights reserved.