聚类算法 - K均值算法

K均值算法介绍

K均值聚类算法计算质心并迭代，直到找到最佳质心。它假设聚类的数量已知。它也称为平面聚类算法。算法从数据中识别出的聚类数量用K均值中的“K”表示。

在此算法中，数据点被分配到一个聚类，使得数据点和质心之间平方距离之和最小。需要理解的是，聚类内部的方差越小，同一聚类内的数据点就越相似。

K均值算法的工作原理

我们可以通过以下步骤了解K均值聚类算法的工作原理：

步骤1 - 首先，我们需要指定此算法需要生成的聚类数量K。
步骤2 - 接下来，随机选择K个数据点并将每个数据点分配给一个聚类。简单来说，就是根据数据点的数量对数据进行分类。
步骤3 - 现在它将计算聚类质心。
步骤4 - 接下来，继续迭代以下步骤，直到我们找到最佳质心，即数据点到聚类的分配不再发生变化：

4.1 - 首先，计算数据点和质心之间平方距离之和。

4.2 - 现在，我们必须将每个数据点分配到比其他聚类（质心）更接近的聚类。

4.3 - 最后，通过取该聚类中所有数据点的平均值来计算聚类的质心。

K均值采用期望最大化方法来解决问题。期望步骤用于将数据点分配给最近的聚类，最大化步骤用于计算每个聚类的质心。

使用K均值算法时，需要注意以下几点：

在使用包括K均值在内的聚类算法时，建议标准化数据，因为此类算法使用基于距离的度量来确定数据点之间的相似性。
由于K均值的迭代性质和质心的随机初始化，K均值可能会停留在局部最优，而可能无法收敛到全局最优。因此，建议使用不同的质心初始化。

Python实现

以下两个实现K均值聚类算法的示例将帮助我们更好地理解它：

示例1

这是一个简单的例子，用于理解K均值的工作原理。在这个例子中，我们将首先生成一个包含4个不同blob的二维数据集，然后应用K均值算法来查看结果。

首先，我们将从导入必要的包开始：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

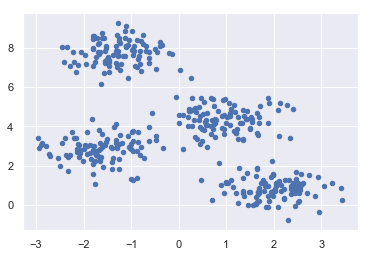
以下代码将生成包含四个blob的二维数据集：

from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)

接下来，以下代码将帮助我们可视化数据集：

plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()

接下来，创建一个KMeans对象，同时提供聚类数量，训练模型并进行预测，如下所示：

kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

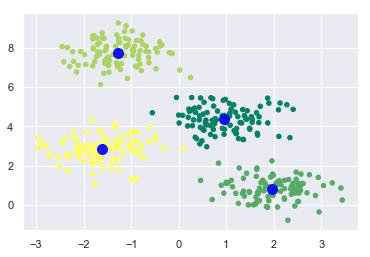
现在，借助以下代码，我们可以绘制并可视化K均值Python估计器选择的聚类中心：

plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()

示例2

让我们来看另一个例子，我们将对简单的数字数据集应用K均值聚类。K均值将尝试在不使用原始标签信息的情况下识别相似的数字。

首先，我们将从导入必要的包开始：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

接下来，从sklearn加载数字数据集并创建它的对象。我们还可以找到此数据集中行数和列数，如下所示：

from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape

输出

(1797, 64)

上面的输出显示，此数据集有1797个样本，具有64个特征。

我们可以像在上面的示例1中一样执行聚类：

kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape

输出

(10, 64)

上面的输出显示，K均值创建了10个具有64个特征的聚类。

fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
   axi.set(xticks=[], yticks=[])
   axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)

输出

作为输出，我们将获得以下图像，显示K均值学习的聚类中心。

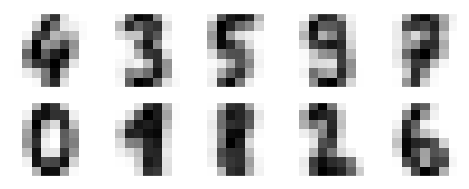
以下几行代码将学习到的聚类标签与其中找到的真实标签匹配：

from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
   mask = (clusters == i)
   labels[mask] = mode(digits.target[mask])[0]

接下来，我们可以检查准确性，如下所示：

from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

输出

0.7935447968836951

上面的输出显示准确率约为80%。

优点和缺点

优点

以下是K均值聚类算法的一些优点：

它很容易理解和实现。
如果我们有很多变量，那么K均值将比层次聚类更快。
重新计算质心时，实例可以更改聚类。
与层次聚类相比，K均值形成更紧密的聚类。

缺点

以下是K均值聚类算法的一些缺点：

很难预测聚类的数量，即k的值。
输出受到初始输入（如聚类数量（k的值））的强烈影响。
数据的顺序将对最终输出产生强烈影响。
它对重新缩放非常敏感。如果我们通过归一化或标准化来重新缩放数据，则输出将完全改变。最终输出。
如果聚类具有复杂的几何形状，它在聚类方面表现不佳。

K均值聚类算法的应用

聚类分析的主要目标是：

从我们正在使用的数据中获得有意义的直觉。
先聚类后预测，其中将为不同的子组构建不同的模型。

为了实现上述目标，K均值聚类表现足够好。它可用于以下应用：

市场细分
文档聚类
图像分割
图像压缩
客户细分
分析动态数据的趋势

打印页面