支持向量机 (SVM)

上一页
下一页

SVM简介

支持向量机（SVM）是一种功能强大且灵活的监督式机器学习算法，可用于分类和回归。但通常，它们用于分类问题。SVM最早在20世纪60年代被提出，但在20世纪90年代得到了完善。与其他机器学习算法相比，SVM有其独特的实现方式。最近，由于其能够处理多个连续和分类变量，因此它们非常受欢迎。

SVM的工作原理

SVM模型基本上是在多维空间中超平面中不同类的表示。超平面将以迭代方式由SVM生成，以便最大程度地减少错误。SVM的目标是将数据集划分为不同的类别以找到最大间隔超平面（MMH）。

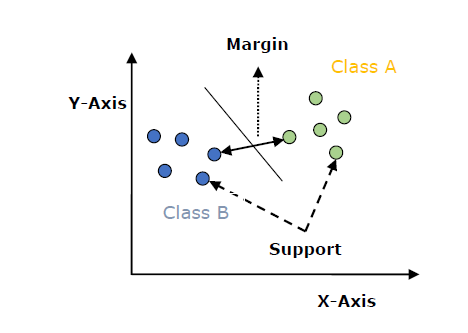
Margin

以下是在SVM中重要的概念：

  • 支持向量 - 最接近超平面的数据点称为支持向量。分离线将借助这些数据点来定义。

  • 超平面 - 正如我们在上图中看到的，它是一个决策平面或空间，它将一组具有不同类别的对象划分开来。

  • 间隔 - 可以定义为不同类别的最近数据点之间的两条线之间的间隙。它可以计算为从线到支持向量的垂直距离。大的间隔被认为是好的间隔，而小的间隔被认为是坏的间隔。

SVM的主要目标是将数据集划分为不同的类别以找到最大间隔超平面（MMH），这可以通过以下两个步骤完成：

  • 首先，SVM将迭代地生成超平面，以最佳方式分离类别。

  • 然后，它将选择正确分离类别的超平面。

在Python中实现SVM

为了在Python中实现SVM，我们将从导入标准库开始，如下所示：

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns; sns.set()

接下来，我们正在创建一个示例数据集，该数据集具有线性可分离的数据，来自sklearn.dataset.sample_generator，用于使用SVM进行分类：

from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=100, centers=2, random_state=0, cluster_std=0.50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');

生成包含100个样本和2个聚类的样本数据集后的输出如下所示：

Map

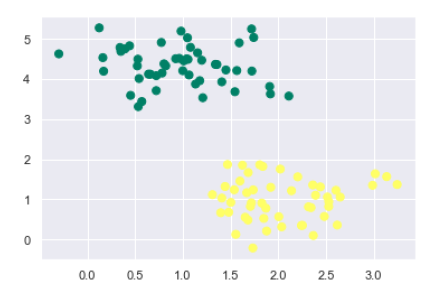
我们知道SVM支持判别式分类。它通过简单地在二维情况下找到一条线或在多维情况下找到一个流形来将类别彼此分开。它在上述数据集上实现如下：

xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
   plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);

输出如下：

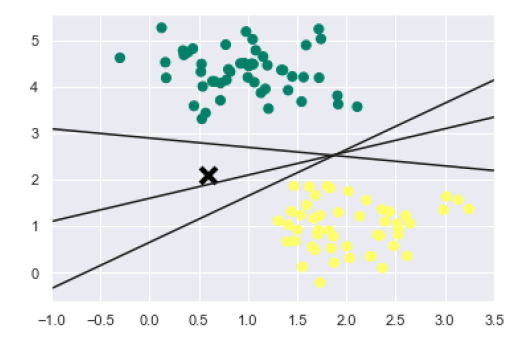
Cross

从上面的输出中我们可以看到，有三个不同的分离器可以完美地区分上述样本。

如上所述，SVM的主要目标是将数据集划分为不同的类别以找到最大间隔超平面（MMH），因此，而不是在类别之间绘制零线，我们可以在每条线的周围绘制一定宽度的间隔，直到最近的点。这可以通过以下方式完成：

xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
   for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
   yfit = m * xfit + b
   plt.plot(xfit, yfit, '-k')
   plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
         color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
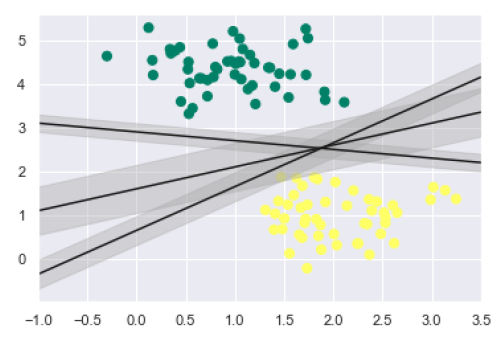
Green

从输出中的上图中，我们可以很容易地观察到判别分类器内的“间隔”。SVM将选择最大化间隔的线。

接下来，我们将使用Scikit-Learn的支持向量分类器在这个数据上训练一个SVM模型。在这里，我们使用线性核来拟合SVM，如下所示：

from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1E10)
model.fit(X, y)

输出如下：

SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)

现在，为了更好地理解，以下将绘制二维SVC的决策函数：

def decision_function(model, ax=None, plot_support=True):
   if ax is None:
      ax = plt.gca()
   xlim = ax.get_xlim()
   ylim = ax.get_ylim()

为了评估模型，我们需要创建网格，如下所示：

x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)

接下来，我们需要绘制决策边界和间隔，如下所示：

ax.contour(X, Y, P, colors='k',
   levels=[-1, 0, 1], alpha=0.5,
   linestyles=['--', '-', '--'])

现在，类似地绘制支持向量，如下所示：

if plot_support:
   ax.scatter(model.support_vectors_[:, 0],
      model.support_vectors_[:, 1],
      s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)

现在，使用此函数拟合我们的模型，如下所示：

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
decision_function(model);
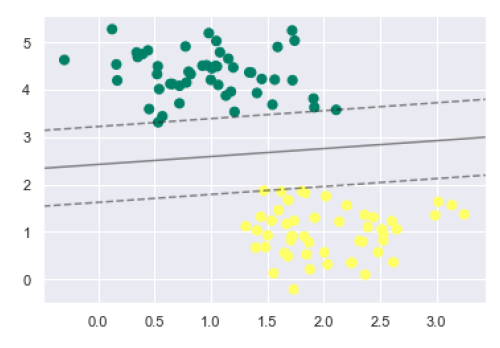
Yellow

从上面的输出中我们可以观察到，一个SVM分类器拟合了具有间隔（即虚线）和支持向量的数据，这些支持向量是此拟合的关键元素，接触到虚线。这些支持向量点存储在分类器的support_vectors_属性中，如下所示：

model.support_vectors_

输出如下：

array([[0.5323772 , 3.31338909],
   [2.11114739, 3.57660449],
   [1.46870582, 1.86947425]])

SVM核函数

在实践中，SVM算法是用核函数实现的，该核函数将输入数据空间转换为所需的形式。SVM使用一种称为核技巧的技术，其中核函数采用低维输入空间并将其转换为高维空间。简单来说，核函数通过向其中添加更多维度将不可分离问题转换为可分离问题。它使SVM更加强大、灵活和准确。以下是SVM使用的一些核函数类型：

线性核函数

它可以用作任何两个观测值之间的点积。线性核函数的公式如下所示：

k(x,xi) = sum(x*xi)

从上面的公式中，我们可以看到两个向量（例如𝑥和𝑥𝑖）之间的乘积是每对输入值的乘积之和。

多项式核函数

它是线性核函数的更一般形式，可以区分曲线或非线性输入空间。以下是多项式核函数的公式：

K(x, xi) = 1 + sum(x * xi)^d

这里d是多项式的次数，我们需要在学习算法中手动指定它。

径向基函数 (RBF) 核函数

RBF核函数主要用于SVM分类，它将输入空间映射到无限维空间。以下公式在数学上解释了它：

K(x,xi) = exp(-gamma * sum((x – xi^2))

这里，gamma的范围是0到1。我们需要在学习算法中手动指定它。gamma的一个好的默认值是0.1。

由于我们为线性可分离数据实现了SVM，因此我们可以使用核函数在Python中为不可分离数据实现它。

示例

以下是使用核函数创建SVM分类器的示例。我们将使用来自scikit-learn的鸢尾花数据集：

我们将从导入以下包开始：

import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as plt

现在，我们需要加载输入数据：

iris = datasets.load_iris()

从此数据集中，我们获取前两个特征，如下所示：

X = iris.data[:, :2]
y = iris.target

接下来，我们将使用原始数据绘制SVM边界，如下所示：

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
   np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]

现在，我们需要提供正则化参数的值，如下所示：

C = 1.0

接下来，可以创建SVM分类器对象，如下所示：

Svc_classifier = svm.SVC(kernel='linear', C=C).fit(X, y)

Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')

输出

Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')
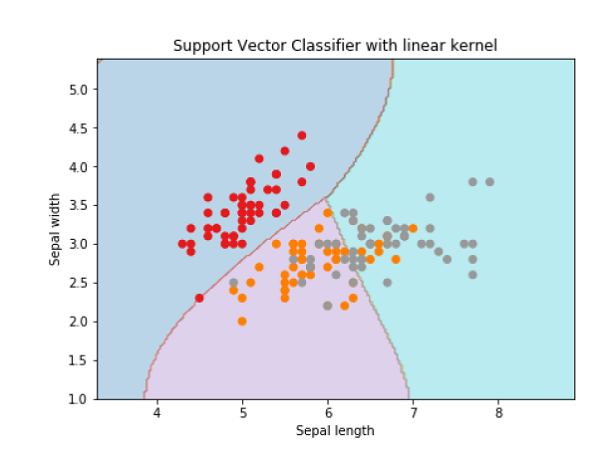
Curve

为了使用rbf核创建SVM分类器，我们可以将核函数更改为rbf，如下所示：

Svc_classifier = svm.SVC(kernel='rbf', gamma =‘auto’,C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')

输出

Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')
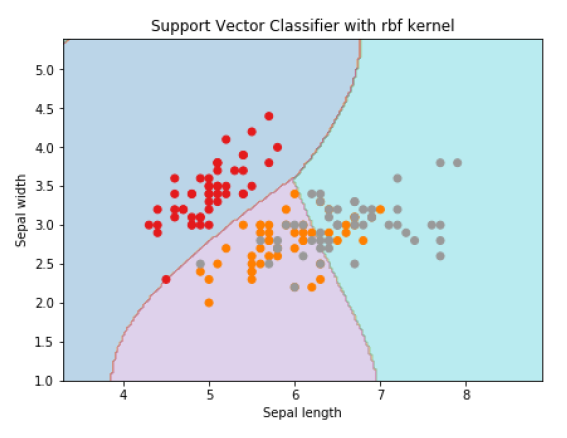
Classifier

我们将gamma的值设置为'auto'，但您也可以提供其值（0到1之间）。

SVM分类器的优缺点

SVM分类器的优点

SVM分类器提供很高的准确性，并且在高维空间中表现良好。SVM分类器基本上使用训练点的一个子集，因此结果使用非常少的内存。

SVM分类器的缺点

它们的训练时间很长，因此在实践中不适合大型数据集。另一个缺点是SVM分类器在处理重叠类别时效果不佳。

打印页面
上一页
下一页
广告