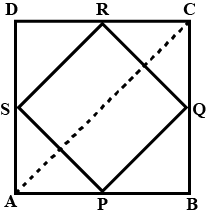
\(ABCD\)是一个四边形，其中\(P、Q、R\)和\(S\)分别是边\(AB、BC、CD\)和\(DA\)的中点（见图8.29）。\(AC\)是一条对角线。证明：
(i) \(SR \parallel AC\) 且 \(SR = \frac{1}{2}AC\)
(ii) \(PQ = SR\)
(iii) \(PQRS\)是一个平行四边形。

"\n

已知

\(ABCD\)是一个四边形，其中\(P、Q、R\)和\(S\)分别是边\(AB、BC、CD\)和\(DA\)的中点。$AC$是一条对角线。

要求

我们必须证明：

(i) \(SR \parallel AC\) 且 \(SR = \frac{1}{2}AC\) (ii) \(PQ = SR\) (iii) \(PQRS\)是一个平行四边形

解答

我们知道：

中点定理指出，连接三角形两边中点的线段平行于第三边，并且长度是第三边的一半。

(i) 在$\triangle DAC$中，$S$是$DA$的中点，$R$是$DC$的中点。因此，根据中点定理，

$SR\parallel AC$ 且 $SR=\frac{1}{2}AC$.....(i)

(ii) 在$\triangle BAC$中，$P$是$AB$的中点，$Q$是$BC$的中点。因此，根据中点定理，

$PQ\parallel AC$ 且 $PQ= \frac{1}{2}AC$。

$PQ=SR$ (由(i))

(iii) $PQ\parallel AC$ 且 $SR\parallel AC$。

因此，$PQ\parallel SR$ 且 $PQ=SR$。

对边相等且平行的四边形是平行四边形。

因此，PQRS是一个平行四边形。

证毕。

Tutorialspoint

更新于：2022年10月10日

88 次浏览

开启你的职业生涯

完成课程获得认证

开始学习