数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究矩形$ABCD$由点$A(-1, -1), B(-1, 4), C(5, 4)$和$D(5, -1)$形成，$P, Q, R$和$S$分别是$AB, BC, CD$和$DA$的中点。四边形$PQRS$是正方形、矩形还是菱形？请说明理由。
已知
$ABCD$是由点$A (-1, -1), B (-1, 4), C (5, 4)$和$D (5, -1)$连接而成的矩形。$P, Q, R$和$S$分别是边$AB, BC, CD$和$DA$的中点。
要求
我们必须确定$PQRS$是正方形、矩形还是菱形。
解答
连接$PR$和$QS$。设$PR$和$QS$的交点为$O$。
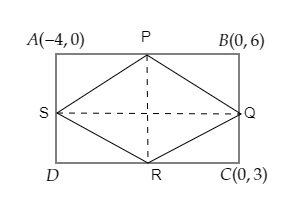
使用中点公式，我们得到：
$P$的坐标为$(\frac{-2}{2}, \frac{3}{2})$
$=(-1, \frac{3}{2})$
类似地，
$Q$的坐标为$(\frac{-1+5}{2}, \frac{4+4}{2})$
$=(\frac{4}{2}, \frac{8}{2})$
$=(2,4)$
$R$的坐标为$(\frac{5+5}{2}, \frac{4-1}{2})$
$=(\frac{10}{2}, \frac{3}{2})$
$=(5, \frac{3}{2})$
$S$的坐标为$(\frac{5-1}{2}, \frac{-1-1}{2})$
$=(\frac{4}{2}, \frac{-2}{2})$
$=(2,-1)$
使用距离公式，我们得到，$\mathrm{PQ}=\sqrt{(2+1)^{2}+(4-\frac{3} {2})^{2}}$
$=\sqrt{(3)^{2}+(\frac{5}{2})^{2}}$
$=\sqrt{9+\frac{25}{4}}$
$=\sqrt{\frac{36+25}{4}}$
$=\sqrt{\frac{61}{4}}$
$=\frac{\sqrt{61}}{2}$
$\mathrm{QR}=\sqrt{(5-2)^{2}+(\frac{3}{2}-4)^{2}}$ $=\sqrt{(3)^{2}+(\frac{-5}{2})^{2}}$
$=\sqrt{9+\frac{25}{4}}$
$=\sqrt{\frac{36+25}{4}}$
$=\sqrt{\frac{61}{4}}$
$=\frac{\sqrt{61}}{2}$
$O$是$PR$的中点。$O$的坐标为$(\frac{-1+5}{2}, \frac{\frac{3}{2}+\frac{3}{2}}{2})$
$=(\frac{4}{2}, \frac{3}{2})$
$=(2, \frac{3}{2})$
类似地，
$\mathrm{O}$是$\mathrm{QS}$的中点，
$O$的坐标为$(\frac{2+2}{2}, \frac{4+(-1)}{2})$
$=(\frac{4}{2}, \frac{3}{2})$
$=(2, \frac{3}{2})$
我们看到，两种情况下$O$的坐标相同，并且邻边也相等。
这意味着它可能是正方形或菱形。
$\mathrm{PR}=\sqrt{(5+1)^{2}+(\frac{3}{2}-\frac{3}{2})^{2}}$
$=\sqrt{(6)^{2}+(0)^{2}}$
$=\sqrt{36+0}$
$=\sqrt{36}$
$=6$
$\mathrm{QS}=\sqrt{(2-2)^{2}+(-1-4)^{2}}$
$=\sqrt{(0)^{2}+(-5)^{2}}$
$=\sqrt{0+25}$
$=\sqrt{25}$
$=5$
这里，对角线不相等。
因此，PQRS是菱形。
54 次浏览
