数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究一个身高 90 厘米的女孩以 1.2 米/秒的速度背离一盏路灯的底部行走。如果路灯距离地面 3.6 米，求 4 秒后她的影子长度。
已知
一个身高 90 厘米的女孩以 1.2 米/秒的速度背离一盏路灯的底部行走。
要求
如果路灯距离地面 3.6 米，我们要求 4 秒后她的影子长度。
解答
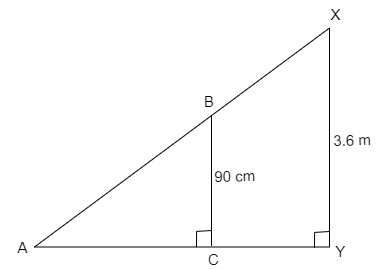
女孩的身高 = 90 厘米 = 0.9 米
路灯的高度 = 3.6 米
女孩的速度 = 1.2 米/秒
所用时间 = 4 秒
4 秒内走过的距离 = 速度 × 时间
CY = 1.2 × 4 = 4.8 米。
设影子的长度 AC 为 x。
在三角形 ABC 和三角形 AXY 中，
∠ACB = ∠AYX = 90°
∠BAC = ∠XAY (公共角)
因此，
三角形 ABC ∽ 三角形 AXY (根据 AA 相似性)
这意味着，
AC/AY = BC/XY (相似三角形的对应边成比例)
x/(x+4.8) = 0.9/3.6
x/(x+4.8) = 1/4
x(4) = 1(x+4.8)
4x = x+4.8
4x-x = 4.8
3x = 4.8
x = 4.8/3
x = 1.6 米
4 秒后她的影子长度为 1.6 米。
更新于：2022 年 10 月 10 日
浏览量 153 次
广告