绘制一个电路图，该电路包含一个由3节2V电池组成的电池组、三个分别为10Ω、20Ω和30Ω的电阻并联连接、一个插头开关和一个电流表，所有元件都串联连接。利用此电路计算以下数值：(a) 每个电阻的电流。(b) 电路中的总电流。(c) 电路的总有效电阻。

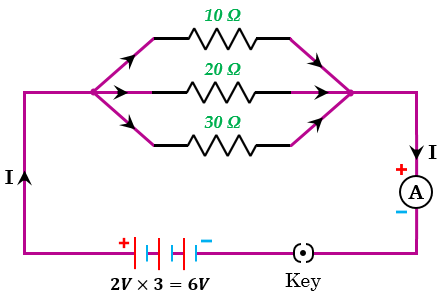
已知

电阻，$R_1=10\Omega$

电阻，$R_2=20\Omega$

电阻，$R_3=30\Omega$

电池节数 $=3$

每节电池电压 =2 V

电池组总电压，$V=2\times {3}=6V$

求解： (a) 每个电阻的电流。

               (b) 电路中的总电流。

               (c) 电路的总有效电阻。

解答： (c) 电路的总有效电阻。

这里，所有电阻都是并联的。

因此，总电阻由以下公式给出：

$\frac {1}{R_E}=\frac {1}{R_1}+\frac {1}{R_2}+\frac {1}{R_3}$

$\frac {1}{R_E}=\frac {1}{10}+\frac {1}{20}+\frac {1}{30}$

$\frac {1}{R_E}=\frac {6+3+2}{60}$

$\frac {1}{R_E}=\frac {11}{60}$

$\frac {1}{R_E}=\frac {11}{60}$

$R_E=\frac {60}{11}$

$R_E=5.45\Omega$

因此，总有效电阻$R_E$为5.45欧姆

解答： (b) 电路中的总电流。

现在，我们知道电路中的总电流由以下公式给出：

$I=\frac {V}{R}$

代入$V$和$R$的值，我们得到：

$I=\frac {6}{5.45}$

$I=\frac {6\times {100}}{545}$

$I=\frac {600}{545}$
$I=1.1A$

因此，电路中的总电流$I$为1.1安培。

解答: (a) 每个电阻的电流。

设电阻$R_1$、$R_2$和$R_3$中的电流分别为$I_1$、$I_2$和$I_3$。

我们知道，在并联连接中，每个电阻两端的电压相同。

电路中的电流$I$由以下公式给出：

$I=\frac {V}{R}$

代入给定值，我们得到：

$I_1=\frac {V}{R_1}\Rightarrow\frac {6}{10}\Rightarrow0.6A$

$I_1=\frac {V}{R_2}\Rightarrow\frac {6}{20}\Rightarrow0.3A$

$I_1=\frac {V}{R_3}\Rightarrow\frac {6}{30}\Rightarrow0.2A$

因此， 

(a) 每个电阻的电流 - 0.6A、0.3A、0.2A。

(b) 电路中的总电流 - 1.1安培。

(c) 电路的总有效电阻 - 5.45欧姆。

教程点

更新于: 2022年10月10日

4K+ 浏览量

开启你的职业生涯

通过完成课程获得认证

开始学习