(a) 利用合适的电路图证明，并联电阻组的等效电阻的倒数等于各个电阻倒数的和。(b) 在一个电路中，两个12 Ω的电阻并联连接到一个6 V的电池上。求电池提供的电流。

(a)

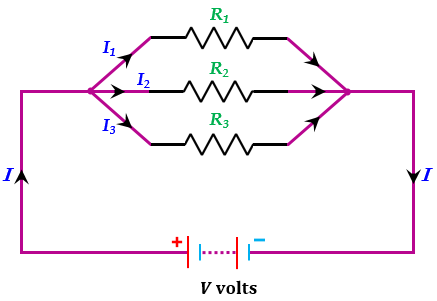
上图显示了一个电路，该电路由三个分别为$R_1$、$R_2$和$R_3$的电阻并联连接到一个电压为$V$的电池上。

假设流过电路的总电流为$I$，则流过电阻$R_1$的电流为$I_1$，流过电阻$R_2$的电流为$I_2$，流过电阻$R_3$的电流为$I_3$。

因此，总电流$I$表示为：

$I=I_1+I_2+I_3$ --------------(i)

由于所有电阻上的电压差相同，因此根据欧姆定律，我们可以得到：

$I_1=\frac {V}{R_1}$

$I_2=\frac {V}{R_2}$

$I_3=\frac {V}{R_3}$

设该并联组合的等效电阻为$R_{eq}$。

因此，根据欧姆定律，整个电路可以表示为：

$I=\frac {V}{R_{eq}}$

现在，

将电流$I$、$I_1$、$I_2$和$I_3$的值代入方程(i)，我们得到：

$\frac {V}{R_{eq}}=\frac {V}{R_1}+\frac {V}{R_2}+\frac {V}{R_3}$

$\frac {1}{R_{eq}}=\frac {1}{R_1}+\frac {1}{R_2}+\frac {1}{R_3}$ $(V=1，因为整个电路中的电压相同)$

因此，已证明，并联电阻组的等效电阻的倒数等于各个电阻倒数的和。

(b) 已知

第一个电阻的阻值为：$R_1=12\Omega$

第二个电阻的阻值为：$R_2=12\Omega$

电压，$V=6V$

求解：电池提供的电流，$I$。

解

我们知道，并联电路中的等效电阻表示为：

$\frac {1}{R_{eq}}=\frac {1}{R_1}+\frac {1}{R_2}$

将$R_1$和$R_2$的值代入公式，我们得到：

$\frac {1}{R_{eq}}=\frac {1}{12}+\frac {1}{12}$

$\frac {1}{R_{eq}}=\frac {1+1}{12}$

$\frac {1}{R_{eq}}=\frac {2}{12}$

$\frac {1}{R_{eq}}=\frac {1}{6}$

$R_{eq}=6\Omega$

因此，等效电阻为6 欧姆。

现在，

为了求出电池提供的电流，我们使用欧姆定律，表示为：

$V=I\times R$

可以重新排列为：

$I=\frac {V}{R}$

代入$V$和$R$的值，我们得到：

$I=\frac {6}{6}$ $(\because R=R_{eq})$

$I=1A$

因此，电池提供的电流为1 安培。

Tutorialspoint

更新于：2022年10月10日

浏览量：181

启动您的职业生涯

完成课程获得认证

开始