画一个75°的∠POQ，并找出它的对称轴。

待办事项

我们需要画一个75°的∠PQR，并找出它的对称轴。

解：

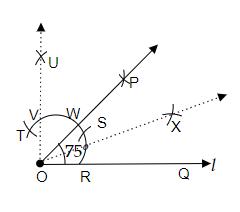
作图步骤

(i) 我们画一条任意长度的直线l，并在直线l上标记两个点O和Q，它们之间的距离可以是任意的。

(ii) 现在，以O点为圆心，任意长度l为半径画弧，并标记弧与直线l的交点为R。

(iii) 现在，以R点为圆心，与之前相同的半径画弧，
并标记该弧与前一个弧的交点为S。

(iv) 现在，以S点为圆心，与之前相同的半径画弧，并标记该弧与前一个弧的交点为T。

(v) 现在，以P和S点为圆心，与之前相同的半径画弧，并标记这两条弧的交点为U，然后连接O和U。

(vi) $\overline{OU}$与弧相交于一点，我们将其命名为V。现在，以S到V的距离的一半以上的半径为圆心，分别以S和V为圆心画弧，这两条弧相交于一点，我们将其命名为P。

(vii) 现在，连接P点和O点。因此，$\overline{OP}$是75°角的对称轴。

(viii) $\overline{OP}$与从O点画出的弧相交于一点，我们将其命名为W。

(ix) 现在，以RW长度的一半以上的半径为圆心，分别以R和W为圆心，在75°角内画弧，靠近直线l。现在，我们标记该弧的交点为X，然后连接O和X。

(x) 因此，$\overline{OX}$是∠PQR=75°的对称轴。

教程点

更新于： 2022年10月10日

43 次查看

开启你的职业生涯

完成课程获得认证

开始学习