求连接点(7, 1)和(3, 5)的线段的垂直平分线的方程。

已知

已知点为(7, 1)和(3, 5)。

要求

我们需要找到连接点(7, 1)和(3, 5)的线段的垂直平分线的方程。

解答

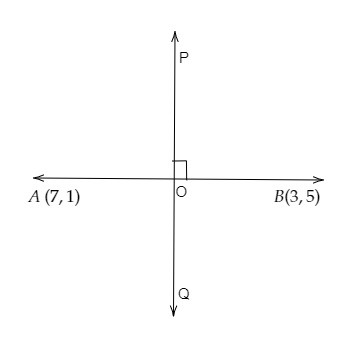
设给定点为A(7,1)和B(3,5)，垂直平分线为PQ。

根据中点公式：

AB的中点O的坐标为：

$=(\frac{7+3}{2}, \frac{1+5}{2})=(5,3)$

AB的斜率$m_{1}$为$=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-1}{3-7}$

$=\frac{4}{-4}=-1$

垂直于AB的直线的斜率$m_{2}$为

$=\frac{-1}{m_{1}}=\frac{-1}{-1}=1$

因此：

垂直平分线的方程为：

$y-y_{1}=m(x-x_{1})$

$\Rightarrow y-3=1(x-5)$

$\Rightarrow y-3=x-5$

$\Rightarrow x-y=-3+5$

$\Rightarrow x-y-2=0$

连接点(7, 1)和(3, 5)的线段的垂直平分线的方程是x-y-2=0。

Tutorialspoint

更新于：2022年10月10日

浏览量 3K+

开启您的职业生涯

完成课程获得认证

开始学习